Volumen berechnen – Formeln und Beispiele

Das Volumen gibt den Rauminhalt eines Körpers an und wird für verschiedene geometrische Formen berechnet. Lerne, wie man das Volumen von Quader, Würfel, Pyramide, Kugel und mehr bestimmt.

Inhaltsverzeichnis zum Thema Volumen berechnen

Das Volumen im Überblick

  • Das Volumen gibt den Rauminhalt eines geometrischen Körpers an.
  • Die SI-Einheit des Volumens ist Kubikmeter \left(\text{m}^3\right).
  • Für die Berechnung des Volumens werden in den meisten Fällen die Grundfläche und die Höhe des Körpers verwendet.
  • Die genaue Berechnungsformel unterscheidet sich je nach Art des Körpers.
Volumen und Volumen berechnen: Lernvideo

Quelle sofatutor.com

Volumen – Erklärung

Der räumliche Inhalt eines geometrischen Körpers wird als Volumen bezeichnet. Es wird auch Raum- oder Kubikinhalt genannt. 

Mit dem Volumen können wir zum Beispiel bestimmen, wie viel Wasser in einen Körper passt oder wie viel Wasser verdrängt wird, wenn ein Körper ins Wasser gelegt wird. 

Volumen – Einheit

Die Einheit vom Volumen beginnt meistens mit Kubik. Die SI-Einheit vom Volumen ist Kubikmeter \left(\text{m}^3\right). Weitere Einheiten sind:

  • Kubikmillimeter \left(\text{mm}^3\right)
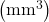
  • Kubikzentimeter \left(\text{cm}^3\right)
  • Kubikdezimeter \left(\text{dm}^3\right)

Für Flüssigkeiten wird häufig die spezielle Einheit Liter \left(\ell \right) verwendet.
Für die Umrechnung der Einheiten gilt:

1~\text{m}^3 = 1\,000~\text{dm}^3
1~\text{dm}^3 = 1\,000~\text{cm}^3
1~\text{dm}^3 = 1~\ell = 1\,000~\text{m}\ell
1~\text{cm}^3 = 1\,000~\text{mm}^3

Bei der Berechnung des Volumens muss immer darauf geachtet werden, dass die Einheiten der einzelnen Faktoren übereinstimmen.

Volumen (Rauminhalt) berechnen – Formeln

Die Berechnung des Volumens (Rauminhalts) eines Körpers hängt von dessen Form ab. In den meisten Fällen spielen die Höhe und die Grundfläche des Körpers eine Rolle. Für die Berechnung des Volumens sind diese drei Abkürzungen wichtig:

V = Volumen
h = Höhe des Körpers
G = Grundfläche des Körpers

In den folgenden Abschnitten betrachten wir die Volumenformeln für einige besondere Körper.

Volumen eines Quaders berechnen

Das Volumen eines Quaders berechnen wir mit der Formel:

V = G \cdot h = a \cdot b \cdot h

Dabei sind a und b die Kantenlängen der Grundfläche.

Volumen Quader

Beispiel
a = 4~\text{cm}
b = 5~\text{cm}
h = 7~\text{cm}

G = a \cdot b = 4~\text{cm} \cdot 5~\text{cm} = 20~\text{cm}^2
V = G \cdot h = 20~\text{cm}^2 \cdot 7~\text{cm} = 140~\text{cm}^3

Volumen eines Würfels berechnen

Bei einem Würfel sind alle Kanten gleich lang. Länge, Breite und Höhe unterscheiden sich somit nicht. Wollen wir das Volumen eines Würfels ausrechnen, nutzen wir die Formel:

V = a^3 = a \cdot a \cdot a

Dabei ist a die Kantenlänge des Würfels.

Volumen Würfel

Beispiel
a = 5~\text{cm}

V = a^3 = \left(5~\text{cm}\right)^3 = 125~\text{cm}^3

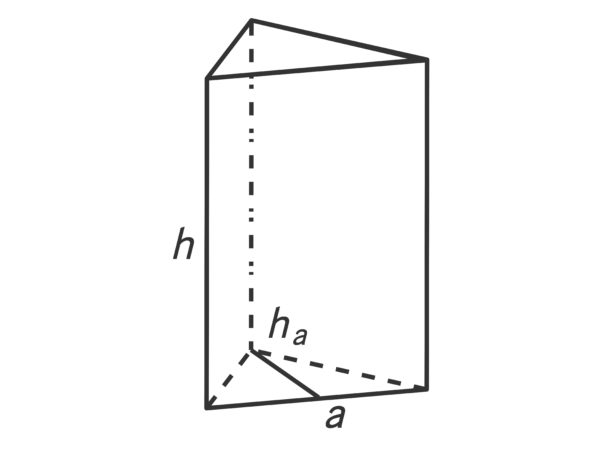
Volumen eines Prismas berechnen

Allgemein berechnet sich das Volumen von Prismen als Grundfläche mal Höhe:

V = G \cdot h

Hat das Prisma eine dreieckige Grundfläche, lautet die Volumenformel:

V = \dfrac{1}{2} \cdot a \cdot h_a \cdot h

Dabei ist a die Grundseite der dreieckigen Grundfläche und h_a die Höhe des Grunddreiecks.

Volumen Prisma

Beispiel
a = 4,\!5~\text{m}
a_h = 4~\text{m}
h = 6~\text{m}

V = \dfrac{1}{2} \cdot a \cdot h_a \cdot h = \dfrac{1}{2} \cdot 4,\!5~\text{m} \cdot 4~\text{m} \cdot 6~\text{m} = 54~\text{m}^3

Volumen einer Pyramide berechnen

Die Berechnung des Volumens einer Pyramide ergibt sich aus der Form ihrer Grundfläche.

Für quadratische Pyramiden gilt:

V = \dfrac{1}{3} \cdot a^2 \cdot h

Volumen quadratische Pyramide

Dabei ist a die Kantenlänge der Grundfläche.

Für Pyramiden mit einem regulären Sechseck als Grundfläche gilt:

V = \dfrac{1}{3} \cdot \dfrac{3 \cdot \sqrt{3} \cdot a^2}{2} \cdot h

Hier bezeichnet a die Kantenlänge des Sechsecks.

Beispiel quadratische Pyramide
a = 3~\text{dm}
h = 5~\text{dm}

V = \dfrac{1}{3} \cdot a^2 \cdot h = \dfrac{1}{3} \cdot \left(3~\text{dm}\right)^2 \cdot 5~\text{dm} = 15~\text{dm}^3

Beispiel sechseckige Pyramide
a = 15~\text{mm}
h = 23~\text{mm}

V = \dfrac{1}{3} \cdot \dfrac{3 \cdot \sqrt{3} \cdot a^2}{2} \cdot h = \dfrac{1}{3} \cdot \dfrac{3 \cdot \sqrt{3} \cdot 15~\text{mm}^2}{2} \cdot 23~\text{mm} \approx 4\,481,\!7~\text{mm}^3

Volumen eines Zylinders berechnen

Wollen wir das Volumen eines Zylinders errechnen, nutzen wir die Formel:

V = \pi \cdot r^2 \cdot h

Dabei ist r der Radius der Grundfläche.

Volumen Zylinder

Beispiel
r = 6~\text{cm}
h = 7~\text{cm}

V = \pi \cdot r^2 \cdot h = \pi \cdot \left(6~\text{cm}\right)^2 \cdot 7~\text{cm} \approx 791,\!7~\text{cm}^3

Volumen eines Kegels berechnen

Um das Volumen eines Kegels zu bestimmen, verwenden wir die Formel:

V = \dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h

Dabei ist r der Radius der Grundfläche.

Volumen Kegel

Beispiel
r = 5~\text{cm}
h = 7~\text{cm}

V = \dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h = \dfrac{1}{3} \cdot \pi \cdot \left(5~\text{cm}\right)^2 \cdot 7~\text{cm} \approx 183,\!3~\text{cm}^3

Volumen einer Kugel berechnen

Das Volumen einer Kugel berechnen wir mit der Formel:

V = \dfrac{4}{3} \cdot \pi \cdot r^3

Dabei ist r der Radius der Kugel.

Volumen Kugel

Beispiel
r = 2,\!5~\text{dm}

V = \dfrac{4}{3} \cdot \pi \cdot r^3 = \dfrac{4}{3} \cdot \pi \cdot \left(2,\!5~\text{dm}\right)^3 \approx 65,\!5~\text{dm}^3

Volumen von Körpern berechnen – Zusammenfassung

Wollen wir das Volumen eines Körpers berechnen, müssen wir die für den Körper entsprechende Formel wählen. Die folgende Tabelle fasst noch einmal die Volumenformeln für die wichtigsten Körper zusammen.

Geometrischer Körper Formel für die Volumenberechnung
Quader V = a \cdot b \cdot h
Würfel V = a^3
Prisma V = \dfrac{1}{2} \cdot G \cdot h
Pyramide V = \dfrac{1}{3} \cdot G \cdot h
Zylinder V = \pi \cdot r^2 \cdot h
Kegel V = \dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h
Kugel V = \dfrac{4}{3} \cdot \pi \cdot r^3

Häufig gestellte Fragen zum Thema Volumen

Die SI-Einheit des Volumens ist Kubikmeter \left(\text{m}^3\right).

Neben Kubikmeter \left(\text{m}^3\right) sind weitere typische Einheiten für das Volumen:

  • Kubikmillimeter \left(\text{mm}^3\right),
  • Kubikzentimeter \left(\text{cm}^3\right),
  • Kubikdezimeter \left(\text{dm}^3\right) und
  • Liter \left(\ell \right).

Die Formeln zur Berechnung des Volumens eines Körpers unterscheiden sich je nach Form des Körpers. In den meisten Fällen wird die Grundfläche mit der Höhe multipliziert. Es existieren jedoch auch Ausnahmen, unter anderem die Kugel.

Das Volumen eines Würfels berechnen wir mit der Formel V = a^3, wobei a die Kantenlänge des Würfels ist.

Sind die Einheiten der einzelnen Faktoren (Höhe, Seitenlänge, Radius …) in Meter \left(\text{m}\right) gegeben oder lassen sich darin umwandeln, erhalten wir das Volumen nach der Berechnung in Kubikmeter \left(\text{m}^3\right).

Die Einheit Liter entspricht der Einheit Kubikdezimeter \left(1~\text{dm}^3 = 1~\ell \right). Sind die Faktoren in der Einheit Dezimeter gegeben, kann das Volumen in der Einheit Liter berechnet werden.

Das Volumen ist dreidimensional, weshalb die Höhe bei der Berechnung auch eine Rolle spielt. Es beschreibt, wie viel Raum ein Körper einnimmt. Die Fläche ist hingegen nur zweidimensional. Sie besitzt nur eine Länge und eine Breite.

Volumen und Masse hängen eng miteinander zusammen. Die Masse wird in Kilogramm gemessen, wohingegen das Volumen in Kubikmeter gemessen wird. Das Volumen gibt an, wie viel Raum ein Körper einnimmt. Die Masse ist hingegen ein Maß der Trägheit eines Körpers. Der physikalische Zusammenhang zwischen Masse und Volumen eines Körpers wird durch die Dichte (Masse/Volumen) beschrieben.

Leave A Comment

Alle Artikel aus dem Fach Mathematik