Quadratische Gleichungen – Erklärung
Erfahre, dass quadratische Gleichungen mindestens eine Variable mit Potenz enthalten. Entdecke verschiedene Formen wie Normal- und reinquadratische Form. Lerne, wie man sie löst, sei es mit der Mitternachts- oder -Formel. Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Quadratische Gleichungen
Wie willst du heute lernen?
Quadratische Gleichungen – Definition
Quadratische Gleichungen sind Gleichungen, in denen mindestens eine Variable mit der Potenz ![]() vorkommt (Beispiel:
vorkommt (Beispiel: ![]() ). In quadratischen Gleichungen kommen keine höheren Potenzen als
). In quadratischen Gleichungen kommen keine höheren Potenzen als ![]() (Beispiel:
(Beispiel: ![]() ) vor.
) vor.
Quadratische Gleichungen können keine, eine oder zwei Lösungen haben. Die Menge der Lösungen einer quadratischen Gleichung wird Lösungsmenge ![]() genannt und geschrieben als:
genannt und geschrieben als:
 (keine Lösung),
(keine Lösung), (eine Lösung) oder
(eine Lösung) oder (zwei Lösungen).
(zwei Lösungen).
Die unterschiedliche Anzahl der Lösungen hängt damit zusammen, dass eine quadratische Potenz vorliegt. Dabei müssen wir beim Auflösen in der Regel eine Wurzel ziehen. Beim Ziehen einer Wurzel kommen immer zwei Ergebnisse heraus:
![]() und
und ![]()
Ausnahme ist die Wurzel aus null: ![]() . Steht unter der Wurzel eine Null, hat die quadratische Gleichung nur eine Lösung.
. Steht unter der Wurzel eine Null, hat die quadratische Gleichung nur eine Lösung.
Zudem kann aus negativen Zahlen keine Wurzel gezogen werden. Steht unter der Wurzel eine negative Zahl, hat die quadratische Gleichung keine Lösung. Die Lösungsmenge ist dann leer:
![]()
Der Unterschied zwischen linearen und quadratischen Gleichungen ist zum einen die Potenz von ![]() und zum anderen die Anzahl der möglichen Lösungen.
und zum anderen die Anzahl der möglichen Lösungen.
Quadratische Gleichungen – Formen
Quadratische Gleichungen lassen sich in verschiedenen Formen darstellen. Die verschiedenen Formen sind unterschiedliche Schreibweisen und können jeweils ineinander umgewandelt werden.
Die allgemeine Form der quadratischen Gleichung lautet:
![]()
Dabei sind ![]() ,
, ![]() und
und ![]() Variablen, für die beliebige reelle Zahlen eingesetzt werden können.
Variablen, für die beliebige reelle Zahlen eingesetzt werden können.
Ist ![]() , sprechen wir von der Normalform der quadratischen Gleichung. Sie wird meist folgendermaßen geschrieben:
, sprechen wir von der Normalform der quadratischen Gleichung. Sie wird meist folgendermaßen geschrieben:
![]()
Dabei sind ![]() und
und ![]() ebenfalls Variablen, für die beliebige reelle Zahlen eingesetzt werden können.
ebenfalls Variablen, für die beliebige reelle Zahlen eingesetzt werden können.
Die allgemeine Form kann in die Normalform umgewandelt werden, indem der gesamte Term durch ![]() geteilt wird:
geteilt wird:
![]()
![]()
Weitere Formen sind:
- Reinquadratische Form (
 ):
):  mit
mit 
- Produktform:

- Quadratische Gleichung ohne absolutes Glied (
 ):
): 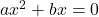
Quadratische Gleichungen lösen
Die Lösungen quadratischer Gleichungen berechnen wir, je nach Form, in der sie gegeben sind, unterschiedlich.
Quadratische Gleichungen in allgemeiner Form lösen
Quadratische Gleichungen in allgemeiner Form lösen wir mit der Mitternachtsformel (![]() -Formel). Die Lösungsformel für quadratische Gleichungen in allgemeiner Form lautet:
-Formel). Die Lösungsformel für quadratische Gleichungen in allgemeiner Form lautet:
![]()
Setzen wir für ![]() ,
, ![]() und
und ![]() die entsprechenden Werte aus der Gleichung ein, dann erhalten wir die Ergebnisse
die entsprechenden Werte aus der Gleichung ein, dann erhalten wir die Ergebnisse ![]() und
und ![]() der quadratischen Gleichung.
der quadratischen Gleichung.
Beispiel 1: ![]()
In dieser quadratischen Gleichung sind ![]() ,
, ![]() und
und ![]() . Setzen wir diese Werte in die Mitternachtsformel ein, dann erhalten wir die folgenden Lösungen:
. Setzen wir diese Werte in die Mitternachtsformel ein, dann erhalten wir die folgenden Lösungen:
![]()
![]()
![]()
Die quadratische Gleichung hat zwei Lösungen:
![]()
Beispiel 2: ![]()
In dieser quadratischen Gleichung sind ![]() ,
, ![]() und
und ![]() . Setzen wir diese Werte in die Mitternachtsformel ein, dann erhalten wir die folgenden Lösungen:
. Setzen wir diese Werte in die Mitternachtsformel ein, dann erhalten wir die folgenden Lösungen:
![]()
Da unter der Wurzel eine Null steht, erhalten wir nur eine Lösung:
![]()
Die quadratische Gleichung hat eine Lösung:
![]()
Quadratische Gleichungen in Normalform lösen
Quadratische Gleichungen in Normalform lösen wir mit der ![]() –Formel. Diese lautet:
–Formel. Diese lautet:
![]()
Setzen wir für ![]() und
und ![]() die entsprechenden Werte aus der Gleichung ein, dann erhalten wir die Ergebnisse
die entsprechenden Werte aus der Gleichung ein, dann erhalten wir die Ergebnisse ![]() und
und ![]() der quadratischen Gleichung.
der quadratischen Gleichung.
Beispiel 1: ![]()
In dieser quadratischen Gleichung sind ![]() und
und ![]() . Die Vorzeichen der Koeffizienten müssen immer beachtet werden. Setzen wir diese Werte in die
. Die Vorzeichen der Koeffizienten müssen immer beachtet werden. Setzen wir diese Werte in die ![]() -Formel ein, erhalten wir die Lösungen:
-Formel ein, erhalten wir die Lösungen:

![]()
![]()
Die Lösungsmenge der quadratischen Gleichung ist:
![]()
Beispiel 2: ![]()
In dieser quadratischen Gleichung sind ![]() und
und ![]() . Setzen wir diese Werte in die
. Setzen wir diese Werte in die ![]() -Formel ein, erhalten wir die Lösungen:
-Formel ein, erhalten wir die Lösungen:

Da die Zahl unter der Wurzel negativ ist, besitzt diese quadratische Gleichung keine Lösung und hat eine leere Lösungsmenge:
![]()
Quadratische Gleichungen in reinquadratischer Form lösen
Ist eine quadratische Gleichung in reinquadratischer Form gegeben, muss diese nur nach ![]() umgestellt werden, um die Gleichung zu lösen.
umgestellt werden, um die Gleichung zu lösen.

Hinweis: Es handelt sich dabei nicht unbedingt um die Wurzel aus einer negativen Zahl. Ist entweder a oder c eine negative Zahl, steht unter der Wurzel eine positive Zahl.
Beispiel: ![]()
Stellen wir diese Gleichung nach ![]() um, erhalten wir die Lösungen:
um, erhalten wir die Lösungen:
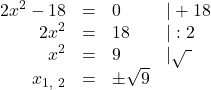
![]()
![]()
Die Lösungsmenge der quadratischen Gleichung ist:
![]()
Quadratische Gleichungen in Punktform lösen
Ist eine quadratische Gleichung in Punktform gegeben, besteht sie aus zwei Faktoren. Ist einer dieser beiden Faktoren null, ist die Gleichung gleich null (Satz vom Nullprodukt). Wir erhalten die Ergebnisse, indem wir schauen, was für ![]() eingesetzt werden muss, damit einer der Faktoren gleich null ist.
eingesetzt werden muss, damit einer der Faktoren gleich null ist.
Beispiel: ![]()
Einer der beiden Faktoren muss null sein, damit die Gleichung erfüllt ist. Daraus ergeben sich die Lösungen:
![]() oder
oder
![]()
Diese quadratische Gleichung hat zwei Lösungen:
![]()
Quadratische Gleichungen lösen – Ausklammern
Besitzt die quadratische Gleichung keine Zahl ohne ![]() , lässt sie sich durch Ausklammern lösen. Das ist der Fall, wenn
, lässt sie sich durch Ausklammern lösen. Das ist der Fall, wenn ![]() (quadratische Gleichung ohne absolutes Glied). Betrachten wir die Vorgehensweise an folgendem Beispiel:
(quadratische Gleichung ohne absolutes Glied). Betrachten wir die Vorgehensweise an folgendem Beispiel:
![]()
Zunächst klammern wir das ![]() aus:
aus:
![]()
Nun handelt es sich um ein Produkt. Die Gleichung ist dann erfüllt, wenn einer der beiden Faktoren gleich null ist (Satz vom Nullprodukt).
![]() oder
oder
![]()
Die erste Lösung ist ![]() . Die zweite Lösung erhalten wir durch Umformen der zweiten Gleichung:
. Die zweite Lösung erhalten wir durch Umformen der zweiten Gleichung:
![]()
Die zweite Lösung ist also ![]() .
.
Die quadratische Gleichung hat die Lösungsmenge:
![]()
Quadratische Gleichungen grafisch lösen
Neben den rechnerischen Lösungswegen gibt es auch zwei Möglichkeiten, die Lösungen näherungsweise grafisch zu bestimmen.
Lösungen mithilfe der Nullstellen ermitteln
Für diese Methode wird die linke Seite einer quadratischen Gleichung der Form ![]() als Funktionsterm einer quadratischen Funktion angenommen. Im Anschluss wird die quadratische Funktion gezeichnet. Die Nullstellen der Funktion, die am Graphen der Funktion abgelesen werden können, entsprechen den Lösungen der quadratischen Gleichung.
als Funktionsterm einer quadratischen Funktion angenommen. Im Anschluss wird die quadratische Funktion gezeichnet. Die Nullstellen der Funktion, die am Graphen der Funktion abgelesen werden können, entsprechen den Lösungen der quadratischen Gleichung.
Beispiel: ![]()
Die dazugehörige Funktionsgleichung lautet: ![]()
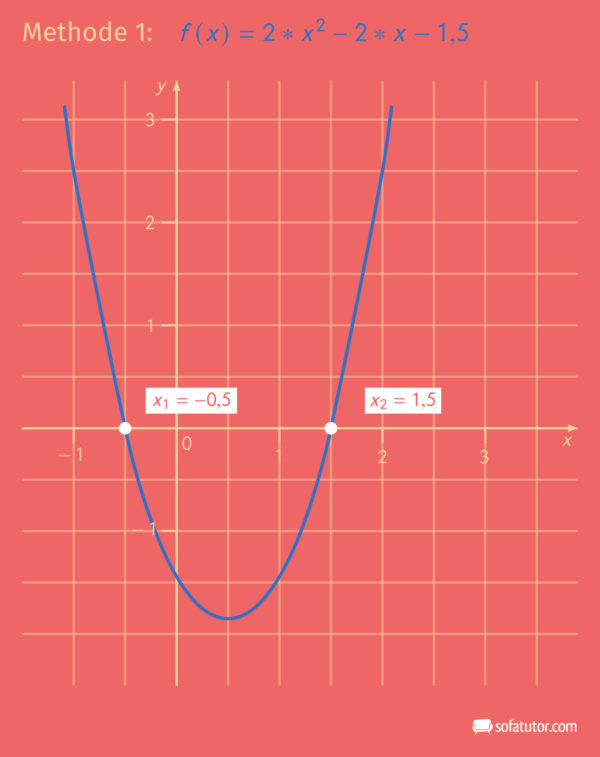
Quelle sofatutor.com
Die Nullstellen der Funktionsgleichung liegen bei ![]() und
und ![]() .
.
Die quadratische Gleichung hat die Lösungsmenge:
![]()
Lösungen über Schnittpunkte ermitteln
Eine zweite Möglichkeit ist es, die Gleichung so umzustellen, dass ![]() allein auf einer Seite der Gleichung steht. Im Anschluss werden beide Seiten der Gleichung als Funktionsterme aufgefasst. Dann werden die Graphen beider Funktionen in ein Koordinatensystem eingezeichnet. Bei der quadratischen Funktion handelt es sich dabei immer um eine Normalparabel. Die Schnittpunkte der beiden Funktionen entsprechen den Lösungen der quadratischen Gleichung.
allein auf einer Seite der Gleichung steht. Im Anschluss werden beide Seiten der Gleichung als Funktionsterme aufgefasst. Dann werden die Graphen beider Funktionen in ein Koordinatensystem eingezeichnet. Bei der quadratischen Funktion handelt es sich dabei immer um eine Normalparabel. Die Schnittpunkte der beiden Funktionen entsprechen den Lösungen der quadratischen Gleichung.
Beispiel: ![]()
Zunächst stellen wir die Gleichung so um, dass ![]() allein steht.
allein steht.

Die beiden Terme werden nun als Funktionsterme eingesetzt:
![]()
![]()
Die Lösungen der quadratischen Gleichung sind die ![]() -Werte der Schnittpunkte dieser beiden Funktionen. Also zeichnen wir die Funktionen in ein Koordinatensystem ein und lesen die Schnittpunkte ab:
-Werte der Schnittpunkte dieser beiden Funktionen. Also zeichnen wir die Funktionen in ein Koordinatensystem ein und lesen die Schnittpunkte ab:

Die Schnittpunkte liegen bei ![]() und
und ![]() .
.
Die Lösungsmenge der quadratischen Gleichung ist somit:
![]()
Quadratische Gleichungen – Aufgaben
Bestimme die Lösungen der folgenden quadratischen Gleichungen:
![]()
![]()
![]()
![]()
Lösung Aufgabe 1: ![]()
Die quadratische Gleichung ![]() ist in Normalform gegeben. Um sie zu lösen, kann die
ist in Normalform gegeben. Um sie zu lösen, kann die ![]() -Formel angewendet werden. In der Gleichung sind
-Formel angewendet werden. In der Gleichung sind ![]() und
und ![]() .
.
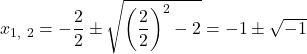
Der Ausdruck unter der Wurzel ist negativ, also existieren keine Lösungen für diese quadratische Gleichung. Die Lösungsmenge ist leer:
![]()
Lösung Aufgabe 2: ![]()
Die quadratische Gleichung ![]() ist in der allgemeinen Form gegeben. Um sie zu lösen, kann die Mitternachtsformel angewendet werden. In der Gleichung sind
ist in der allgemeinen Form gegeben. Um sie zu lösen, kann die Mitternachtsformel angewendet werden. In der Gleichung sind ![]() ,
, ![]() und
und ![]() .
.
![]()
![]()
Diese quadratische Gleichung besitzt nur eine Lösung ![]() . Die Lösungsmenge der quadratischen Gleichung ist:
. Die Lösungsmenge der quadratischen Gleichung ist:
![]()
Lösung Aufgabe 3: ![]()
Die Gleichung ![]() besitzt kein absolutes Glied, kann also durch Ausklammern gelöst werden.
besitzt kein absolutes Glied, kann also durch Ausklammern gelöst werden.
![]()
![]()
Einer der beiden Faktoren muss null sein, damit die Gleichung erfüllt ist.
![]()
![]()
Die quadratische Gleichung hat zwei Lösungen:
![]()
Lösung Aufgabe 4: ![]()
Die Gleichung ![]() ist in reinquadratischer Form gegeben, kann also durch Umformung gelöst werden.
ist in reinquadratischer Form gegeben, kann also durch Umformung gelöst werden.
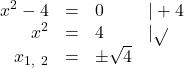
![]()
![]()
Die Lösungsmenge lautet:
![]()
Quadratische Gleichungen – Textaufgaben
Aufgabe 1
Berechne die Seitenlängen eines Rechtecks mit dem Flächeninhalt ![]() , wenn die Seite
, wenn die Seite ![]() doppelt so lang ist wie die Seite
doppelt so lang ist wie die Seite ![]() .
.
Lösung Aufgabe 1
Der Flächeninhalt eines Rechtecks berechnet sich mit der Formel ![]() . Wir wissen
. Wir wissen ![]() und
und ![]() . Beide Informationen können wir in die Gleichung einsetzen:
. Beide Informationen können wir in die Gleichung einsetzen:
![]()
Um die Seitenlänge ![]() zu erhalten, müssen wir diese quadratische Gleichung nach
zu erhalten, müssen wir diese quadratische Gleichung nach ![]() umstellen:
umstellen:
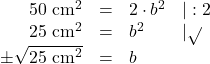
![]()
Bei Anwendungsaufgaben muss immer geschaut werden, wie sinnvoll ein Ergebnis ist. Da die Seitenlänge nicht negativ sein kann, ist nur ![]() realistisch. Mit
realistisch. Mit ![]() kann nun
kann nun ![]() berechnet werden:
berechnet werden:
![]()
Antwortsatz: Das Rechteck hat die Seitenlängen ![]() und
und ![]() .
.
Aufgabe 2
Emmas Zimmer ist ![]() groß und hat eine rechteckige Form. Eine Seite des Zimmers ist zwei Meter länger als die andere Seite. Bestimme die Länge der beiden Seiten!
groß und hat eine rechteckige Form. Eine Seite des Zimmers ist zwei Meter länger als die andere Seite. Bestimme die Länge der beiden Seiten!
Lösung Aufgabe 2
Die Formel für den Flächeninhalt eines Rechtecks lautet: ![]() . Wir wissen, dass das Zimmer eine Fläche von
. Wir wissen, dass das Zimmer eine Fläche von ![]() hat, diesen Wert können wir für
hat, diesen Wert können wir für ![]() in die Formel einsetzen. Außerdem ist eine Seite zwei Meter länger als die andere. Wir können also sagen:
in die Formel einsetzen. Außerdem ist eine Seite zwei Meter länger als die andere. Wir können also sagen: ![]() . Wir erhalten die Formel:
. Wir erhalten die Formel:
![]()
Aufgrund der Übersichtlichkeit lassen wir die Einheiten bei der Berechnung weg. Sowohl ![]() als auch
als auch ![]() haben die Einheit
haben die Einheit ![]() . Diese darf am Ende bei der Antwort nicht vergessen werden.
. Diese darf am Ende bei der Antwort nicht vergessen werden.
Um die Gleichung zu lösen, nutzen wir die ![]() -Formel. Dafür muss die Gleichung so umgestellt werden, dass auf einer Seite null steht:
-Formel. Dafür muss die Gleichung so umgestellt werden, dass auf einer Seite null steht:
![]()
Somit sind ![]() und
und ![]() . Nun kann die Gleichung mit der
. Nun kann die Gleichung mit der ![]() -Formel gelöst werden:
-Formel gelöst werden:

![]()
![]()
Auch hier ist nur ![]() eine sinnvolle Lösung, weil eine Zimmerseite keine negative Länge haben kann. Da wir wissen, dass die Seite
eine sinnvolle Lösung, weil eine Zimmerseite keine negative Länge haben kann. Da wir wissen, dass die Seite ![]() um
um ![]() länger ist, ist
länger ist, ist ![]() .
.
Probe: ![]()
Antwortsatz: Das Zimmer hat die Seitenlängen ![]() und
und ![]() .
.
Häufig gestellte Fragen zum Thema Quadratische Gleichungen









Alle Artikel aus dem Fach Mathematik