Quader in der Grundschule – Definition, Eigenschaften und Beispiele

Ein Quader ist ein geometrischer Körper mit bestimmten Eigenschaften:

• Er hat 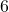rechteckige Flächen.
• Er hat 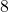Ecken.
• Er hat 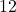Kanten.
• Die sich gegenüberliegenden Flächen sind gleich groß.

Im folgenden Bild sehen wir verschiedene Beispiele für Quader im Schrägbild gezeichnet. Alle haben die vier beschriebenen Merkmale. Dabei stellen wir fest, dass die Quader trotzdem etwas unterschiedlich aussehen können, je nachdem welche Kantenlängen der Quader hat. Ein besonderer Quader ist der Würfel oben rechts, dessen Kantenlängen alle gleich sind.

Beispiele für Quader begegnen uns auch immer wieder im Alltag: Pakete, Bücher oder Koffer haben beispielsweise häufig diese Form.

Die Fläche, auf der der Quader liegt, wird Grundfläche genannt. Alle Außenflächen des Quaders zusammen werden als Oberfläche bezeichnet. 

Alles, was innerhalb dieser Ummantelung liegt, heißt Volumen.
Bei verschiedenen Quadern, wie oben, sind Oberfläche und Volumen aufgrund der verschiedenen Kantenlängen unterschiedlich groß.

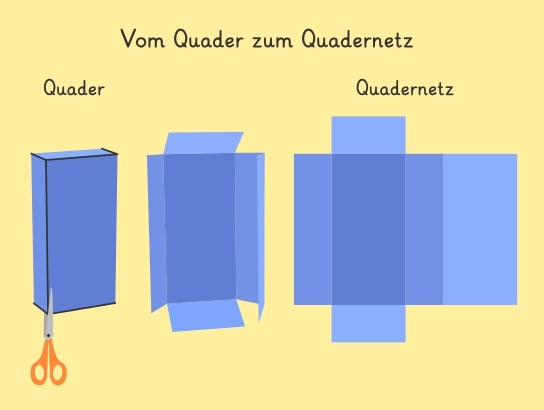
Quader können aus Quadernetzen zusammengebaut werden. Ein Quadernetz entsteht, wenn du einen Quader an den Kanten so aufschneidest, dass eine ebene, zusammenhängende Figur entsteht.

Nun wollen wir einen Quader mit den Kantenlängen , , zeichnen:

1. Zeichne zunächst die Vorderseite als Rechteck (Beispiel: mit den Seitenlängen und ).
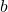2. Zeichne nun in einem 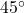-Winkel die nach hinten laufenden vier Kanten: Pro Zentimeter eine Kästchendiagonale (Beispiel: 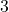Kästchendiagonalen nach hinten, da ). Dabei wird die nicht sichtbare Kante unten links gestrichelt gezeichnet.
3. Für die Rückseite verbinde die hinteren Endpunkte der Kanten. Auch hier zeichnen wir die beiden verdeckten Kanten als gestrichelte Linien.

Im Folgenden gehen wir auf die Volumenberechnung, die Berechnung des Oberflächeninhalts und der Raumdiagonalen eines Quaders ein:

Volumen Quader berechnen
Die Volumenformel für einen Quader mit den Kantenlängen , , lautet:

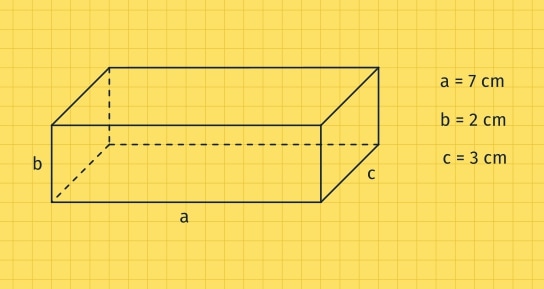
Mit den Kantenlängen aus dem obigen Beispiel erhalten wir:

Die Einheit des Volumens ist Kubikzentimeter.

Oberflächeninhalt Quader berechnen
Der Inhalt der Oberfläche wird berechnet, indem alle Seitenflächen addiert werden. Die Formel lautet:

Aus dem Beispiel:

Raumdiagonale eines Quaders berechnen
Die Raumdiagonale ist die Verbindungslinie von einer Ecke des Quaders zur gegenüberliegenden Ecke, die am weitesten entfernt ist. Sie verläuft damit einmal quer durch den Raum, der vom Quader umgeben ist. Wir können sie mithilfe des Satzes des Pythagoras aus den Kantenlängen und der Diagonalen einer Seitenfläche des Quaders berechnen.