Prozentuale Veränderung berechnen

Ändert sich ein Wert, wie der Preis oder das Gewicht von etwas, kann diese Änderung in Prozent angegeben werden. Wir sprechen dabei von der prozentualen Veränderung. Diese kann für alle möglichen sich ändernden Größen und sowohl für eine Steigerung als auch für eine Verringerung des ursprünglichen Werts berechnet werden.

Bei einer Steigerung gibt die prozentuale Änderung an, wie viel Prozent des ursprünglichen Werts dazugekommen sind. Bei einer Verringerung zeigt die prozentuale Änderung an, wie viel Prozent des ursprünglichen Werts von diesem abgezogen wurden.

Die prozentuale Änderung unterscheidet sich von der tatsächlichen Änderung. Die tatsächliche Änderung hat immer die gleiche Einheit wie die sich ändernden Werte und ist die Differenz zwischen dem ursprünglichen Wert und dem Endwert. Die prozentuale Änderung gibt diese Differenz in Prozent an.

Im Text zur Prozentrechnung findest du alle wichtigen Grundlagen, die du zum Verstehen und Berechnen der prozentualen Änderung benötigst.

Um die prozentuale Änderung zweier Werte zu berechnen, nutzen wir die Formel:

Der Endwert ist der Wert nach der Änderung und der Anfangswert der Wert vor der Änderung.
Die Veränderung berechnen wir mit dieser Formel immer in Prozent. Der Wert ist bei einer prozentualen Steigerung positiv und bei einer prozentualen Verringerung negativ.

Wie wir die prozentuale Veränderung berechnen, schauen wir uns nun noch einmal genauer an den folgenden Beispielaufgaben an.

Betrachten wir zunächst die Anwendung der Formel bei einer prozentualen Steigerung.

Beispiel 1
Lena will sich ein neues Handy kaufen. Letzten Monat hat dieses noch Euro gekostet. Jetzt kostet es jedoch Euro. Es soll die Wertsteigerung des Handys in Prozent berechnet werden. Wir stellen uns also die Frage: Um wie viel Prozent ist der Preis des Handys gestiegen?

Um die prozentuale Erhöhung des Preises auszurechnen, müssen wir zunächst den Anfangswert und den Endwert bestimmen.
Der Endwert ist der jetzige Preis für das Handy, also Euro. Das, was das Handy davor gekostet hat, ist der Anfangswert, also Euro. Setzen wir beide Werte in die Formel ein, können wir den prozentualen Anstieg des Preises berechnen:

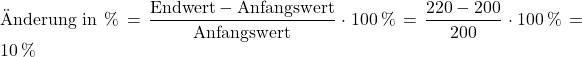
Die prozentuale Änderung beträgt , der Preis des Handys ist also um gestiegen. Die tatsächliche Änderung ist in diesem Fall Euro.

Beispiel 2
Ein Katzenbaby wiegt bei der Geburt . Nach drei Tagen wiegt es bereits . Wie groß ist die Gewichtszunahme in Prozent?

Um die prozentuale Zunahme des Gewichts der Katze zu berechnen, müssen wir auch hier zunächst den Anfangswert und den Endwert festlegen:

Anfangswert (Gewicht bei der Geburt) =
Endwert (Gewicht nach drei Tagen) =

Indem wir beide Werte in die Formel einsetzen, können wir den prozentualen Zuwachs des Gewichts der Katze berechnen.

Die prozentuale Änderung beträgt . Das Gewicht der Katze hat also in den drei Tagen um zugenommen. Die tatsächliche Änderung beträgt in diesem Fall .

Beispiel 3
Luis hat im letzten Monat mit dem Verkauf von selbst gebastelten Ketten Euro Umsatz gemacht. Diesen Monat beträgt sein Umsatz bereits Euro. Wie groß ist seine Umsatzsteigerung?

Um die Umsatzsteigerung zu berechnen, müssen wir auch hier zunächst den Anfangswert und den Endwert festlegen:

Anfangswert (Umsatz im letzten Monat) = Euro
Endwert (Umsatz in diesem Monat) = Euro

Indem wir beide Werte in die Formel einsetzen, erhalten wir die prozentuale Änderung des Umsatzes:

Die prozentuale Änderung beträgt , der Umsatz ist also im Vergleich zum vorherigen Monat um gestiegen. Die tatsächliche Änderung beträgt in diesem Fall Euro.

Bei einer prozentualen Abnahme verwenden wir die gleiche Formel. Allerdings ist das Ergebnis negativ. Schauen wir uns das anhand der folgenden beiden Beispiele genauer an.

Beispiel 1
Eine Jacke kostete im Winter Euro. Jetzt, Ende des Winters, ist sie auf Euro reduziert. Wie groß ist der Rabatt in Prozent?

Auch hier müssen wir zunächst den Anfangs- und den Endwert bestimmen.

Anfangswert (Preis im Winter) = Euro
Endwert (jetziger Preis) = Euro

Setzen wir beide Werte in die Formel ein, können wir die Änderung berechnen:

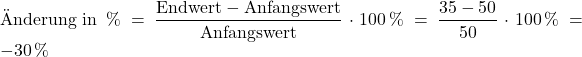
Da es sich um eine Verringerung handelt, ist die prozentuale Änderung negativ, sie beträgt . Wir sagen dann: Die Jacke ist um reduziert.
Die tatsächliche Änderung beträgt in diesem Beispiel Euro.

Beispiel 2
In einem Dorf haben vor Jahren noch Menschen gewohnt. Heute leben nur noch Menschen dort. Wie stark hat die Einwohnerzahl in Prozent abgenommen?

Zunächst bestimmen wir wieder den Anfangs- und den Endwert:

Anfangswert (Einwohnerzahl vor Jahren) =
Endwert (Einwohnerzahl heute) =

Setzen wir beide Werte in die Formel ein, können wir die Änderung berechnen:

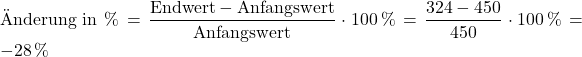
Auch hier erhalten wir wieder eine negative Zahl, da es sich um eine Verringerung handelt. Die prozentuale Änderung beträgt , die Einwohnerzahl hat also um abgenommen.
Die tatsächliche Änderung beträgt in diesem Beispiel Menschen.

Es kann auch vorkommen, dass die prozentuale Änderung und entweder der Anfangs- oder der Endwert gegeben ist. Der jeweils andere Wert ist dann gesucht und muss berechnet werden. Dafür wird die Formel entsprechend umgestellt. Ist der Anfangswert gesucht, lautet die Formel:

Ist der Endwert gesucht, lautet die Formel:

Du kannst die Formel aber auch umstellen, nachdem du die gegebenen Werte eingesetzt hast.

Aufgabe
Luisa hat im letzten Schuljahr Euro Taschengeld bekommen. In diesem Schuljahr bekommt sie mehr Geld. Wie viel Taschengeld bekommt Luisa jetzt?

Zunächst schauen wir, welche Werte uns gegeben sind und welcher Wert gesucht ist.

Gegeben
Anfangswert = Euro
Änderung =

Gesucht: Endwert

Lösung
Da der Endwert gesucht ist, nutzen wir die Formel, bei der dieser allein steht, und setzen die gegebenen Werte ein:

Antwortsatz: Luisa bekommt dieses Schuljahr Euro Taschengeld.

Aufgabe
Die Fläche eines Waldes hat um abgenommen. Jetzt beträgt sie nur noch . Wie groß war die Waldfläche ursprünglich?

Gegeben
Endwert =
Änderung =

Hinweis: Wir nutzen hier einen negativen Prozentwert, da es sich um eine Abnahme handelt.

Gesucht: Anfangswert

Lösung
Setzen wir die Werte in die entsprechende Formel ein, erhalten wir für den Anfangswert:

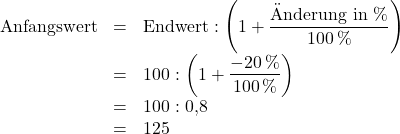
Antwortsatz: Der Wald hatte ursprünglich eine Fläche von .

Ist der Endwert gesucht, kann auch mit dem Prozentfaktor gerechnet werden. Der Prozentfaktor gibt an, um wie viel Prozent sich etwas geändert hat. Bei einer Steigerung berechnet sich der Prozentfaktor, indem die prozentuale Änderung zu den ursprünglichen addiert wird:

Bei einer Verringerung ist die prozentuale Änderung negativ, weshalb sie von den ursprünglichen abgezogen wird:

Bevor wir weiterrechnen können, müssen wir den Prozentfaktor von einer Prozentzahl in eine Dezimalzahl umwandeln, das bedeutet, dass wir durch teilen.

Beispiel:

Den Endwert berechnen wir dann, indem wir den Anfangswert mit dem umgerechneten Prozentfaktor multiplizieren:

Aufgabe
Timo hat Euro auf seinem Konto. Innerhalb eines Jahres kann er es um erhöhen. Wie viel Geld hat er nach einem Jahr auf dem Konto?

Lösung
Zunächst können wir den Prozentfaktor bestimmen. Da es sich um eine Zunahme handelt, addieren wir die Änderung zu den :

Den Endwert berechnen wir nun, indem wir den Anfangswert von Euro mit dem Prozentfaktor multiplizieren:

Antwortsatz: Nach einem Jahr hat Timo Euro auf dem Konto.

Aufgabe
Der Inhalt einer Kekspackung wird vom Hersteller von ursprünglich um reduziert. Wie viel Gramm sind jetzt noch in der Packung?

Lösung
Zunächst können wir den Prozentfaktor bestimmen. Da es sich um eine Abnahme handelt, subtrahieren wir die Änderung von den :

Den Endwert berechnen wir nun, indem wir den Anfangswert von mit dem Prozentfaktor multiplizieren:

Antwortsatz: Die Kekspackung enthält jetzt nur noch .