Lagebeziehung von Geraden und Ebenen in der Geometrie

Lagebeziehung von Geraden und Ebenen: Entdecke, wie sich Geraden und Ebenen im dreidimensionalen Raum zueinander verhalten. Von Schnittpunkten über Parallelen bis hin zur Lage innerhalb der Ebene. Erfahre mehr über die Positionierung von Geraden und Ebenen im folgenden Text!

Inhaltsverzeichnis zum Thema Lagebeziehung Gerade Ebene

Lagebeziehungen Gerade Ebene im Überblick

  • Bei der Lagebeziehung von Geraden und Ebenen gibt es im Wesentlichen drei Fälle: Die Gerade und die Ebene schneiden sich, die Gerade und die Ebene verlaufen parallel zueinander oder die Gerade verläuft innerhalb der Ebene.

  • Mit der Geraden- und Ebenengleichung kann ermittelt werden, ob es einen Schnittpunkt zwischen der Geraden und der Ebene gibt.

  • Besonders einfach ist die Rechnung, wenn die Komponenten der Geradengleichung in die Ebenengleichung in Koordinatenform eingesetzt werden.

Geometrische Lagebezeichnungen – waagerecht, senkrecht, horizontal und vertikal

Quelle sofatutor.com

Lagebeziehung zwischen Ebene und Gerade

Geraden kennst du vielleicht schon aus der zweidimensionalen Geometrie. Im Dreidimensionalen besitzen sie ähnliche Eigenschaften, mit dem Unterschied, dass sie im dreidimensionalen Raum verlaufen. Geraden können beschrieben werden durch eine Geradengleichung der Form g:\vec{x}=\vec{A} + \lambda \cdot \vec{u}. Diese Form wird auch als Parameterform bezeichnet.

Ebenen sind Flächen im dreidimensionalen Raum mit unendlicher Ausdehnung. Auch sie besitzen zugehörige Ebenengleichungen. Eine Ebene kann durch drei Punkte oder zwei Geraden aufgespannt werden. Für die Ebenengleichung gibt es verschiedene Formen:

  • die Parameterform,
  • die Koordinatenform und
  • die Normalenform.

Um herauszufinden, wie die Lagebeziehung einer Geraden zu einer Ebene ist, kannst du die Geradengleichung in die Ebenengleichung einsetzen. Dabei ist es wichtig, dass die Ebenengleichung in Koordinatenform vorliegt.

Das Ergebnis der Gleichung verrät dir, wie Gerade und Ebene zueinander verlaufen.

Ebene und Gerade mit Schnittpunkt

Schnittpunkt von Ebene und Gerade

Eine Ebene und eine Gerade können sich in einem Punkt schneiden. Dieser Fall liegt vor, wenn du aus der Gleichung einen eindeutigen Wert für den Parameter \lambda ermitteln kannst.
Setzt du diesen Wert in die Geradengleichung ein, erhältst du die Koordinaten des Schnittpunkts von Gerade und Ebene.

Betrachte beispielsweise die Gerade g:\vec{x}= \begin{pmatrix} 3\\ 3 \\ 0 \end{pmatrix}+ \lambda \cdot \begin{pmatrix} -3 \\ -3 \\ 4 \end{pmatrix} und die Ebene E: -2x_2+3x_3=6.

Wir setzen die einzelnen Komponenten aus der Geradengleichung für x_1, x_2 und x_3 in die Ebenengleichung ein:

-2\cdot(3+\lambda \cdot (-3))+3\cdot(0+\lambda \cdot 4) = 6

Löse diese Gleichung nach \lambda auf:

\begin{array}{rcll} -6+6 \lambda+12 \lambda &=& 6 &\quad \vert +6\\ 18 \lambda &=& 12 &\quad \vert :18 \\\ \lambda &=& \dfrac{12}{18} = \dfrac{2}{3} & \end{array}

Setzt du diesen Wert für \lambda in die Geradengleichung ein, erhältst du die Koordinaten des Schnittpunkts der Geraden g und der Ebene E:

\begin{pmatrix} 3\\ 3 \\ 0 \end{pmatrix}+ \dfrac{2}{3} \cdot \begin{pmatrix} -3 \\ -3 \\ 4 \end{pmatrix} = \begin{pmatrix} 3\\ 3 \\ 0 \end{pmatrix}+ \begin{pmatrix} -2 \\ -2 \\ 2,\!67 \end{pmatrix} = \begin{pmatrix} 1\\ 1 \\ 2,\!67 \end{pmatrix}

Hinweis: Eine Gerade kann eine Ebene im rechten Winkel schneiden. Man sagt dann, dass Gerade und Ebene orthogonal zueinander sind. Ob das der Fall ist, kannst du überprüfen, indem du das Skalarprodukt des Richtungsvektors der Geraden mit einem Normalenvektor der Ebene berechnest. Ist das Skalarprodukt null, sind Ebene und Gerade orthogonal zueinander – und umgekehrt.

Parallele Geraden und Ebenen

Ebene und parallel Gerade mit konstantem Abstand

Eine Gerade g und eine Ebene E können parallel zueinander verlaufen. In diesem Fall haben g und E keinen Schnittpunkt. Die Gleichung, die du durch Einsetzen der Geradengleichung in die Ebenengleichung erhältst, ist für kein \lambda erfüllt.

Bei der Geraden g:\vec{x}=\begin{pmatrix} 0\\ 3 \\ 0 \end{pmatrix}+ \lambda \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} und der Ebene E: x_2=0 ist dies der Fall.

Die Geradengleichung in die Ebenengleichung eingesetzt ergibt:

3+ \lambda \cdot 0=0

Da 3=0 keine wahre Aussage ist, gibt es keine reelle Zahl \lambda, die die Gleichung erfüllt. Daher sind Gerade und Ebene parallel.

Gerade liegt in der Ebene

Gerade verläuft in Ebene

Liegt die Gerade innerhalb der Ebene, gibt es unendlich viele Schnittpunkte. Die Gleichung, die du durch Einsetzen der Geradengleichung in die Ebenengleichung erhältst, ist in diesem Fall für jedes \lambda erfüllt.

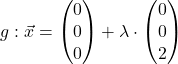Betrachte als Beispiel noch einmal die Ebene E: x_2=0. Welche Lage hat die Gerade g:\vec{x}=\begin{pmatrix} 0\\ 0 \\ 0 \end{pmatrix}+ \lambda \cdot \begin{pmatrix} 0 \\ 0 \\ 2 \end{pmatrix} zu der Ebene?
Setze die Geradengleichung in die Ebenengleichung ein:

0+\lambda \cdot 0=0

Diese Gleichung ist für jedes beliebige \lambda erfüllt, da die Aussage 0 = 0 immer wahr ist. Die Gerade liegt also innerhalb der Ebene.

Übersicht der Lagebeziehungen von Geraden & Ebenen im dreidimensionalen Raum

Um die Lagebeziehung zwischen Ebene und Gerade zu bestimmen, setzen wir die einzelnen Zeilen der Geradengleichung für die Koordinaten x_1, x_2 und x_3 in die Ebenengleichung in Parameterform ein und lösen nach dem verbleibenden Parameter \lambda aus der Geradengleichung auf.
In der folgenden Tabelle sind die verschiedenen Lagebeziehungen von Geraden und Ebenen zusammengefasst.

Lagebeziehung Schnittpunkte Lösung
Ebene und Gerade verlaufen parallel zueinander. kein Schnittpunkt Gleichung für kein \lambda erfüllt
Ebene und Gerade schneiden sich. genau ein Schnittpunkt Gleichung für genau einen Wert für \lambda erfüllt
Gerade liegt in Ebene. unendlich viele Schnittpunkte Gleichung für jedes beliebige \lambda erfüllt

Übersicht der Lagebeziehungen von Geraden und Ebenen in räumlichen Figuren

Die Kanten und Flächen geometrischer Körper liegen in Geraden bzw. Ebenen. Diese Geraden und Ebenen können durch Terme beschrieben werden.

Ein geometrischer Körper ist als räumliche Figur von Geraden und Ebenen begrenzt. Diese Geraden und Ebenen schneiden sich in Eckpunkten des Körpers.

Würfel im dreidimensionalen Koordinatensystem

Häufig gestellte Fragen zum Thema Lagebeziehung Gerade Ebene

Geraden und Ebenen verlaufen im dreidimensionalen Raum. Sie können unterschiedlich zueinander liegen. Die verschiedenen Fälle, die dabei auftreten, werden Lagebeziehungen genannt.

Durch das Einsetzen der Geradengleichung in die Koordinatenform der Ebenengleichung kann bestimmt werden, wie eine Gerade zu einer Ebene verläuft. Dabei ist ausschlaggebend, welche Lösungen die resultierende Gleichung hat.

Die Lagebeziehung einer Geraden und einer Ebene kannst du bestimmen, indem du die Geradengleichung in die Ebenengleichung einsetzt. Du erhältst dadurch eine neue Gleichung. Die Lösungen dieser Gleichung verraten dir, wie die Gerade und die Ebene zueinander liegen.

Es wird unterschieden zwischen drei verschiedenen Lagebeziehungen:

  • Die Gerade schneidet die Ebene in einem Punkt.
  • Die Gerade verläuft parallel zur Ebene.
  • Die Gerade verläuft innerhalb der Ebene.

Eine Ebene ist eine unendlich erweiterbare Fläche im dreidimensionalen Raum. Die Gerade ist eine gerade Linie, die sowohl im zweidimensionalen als auch im dreidimensionalen Raum verlaufen kann und ebenfalls unendlich verlängert werden kann.

Leave A Comment

Alle Artikel aus dem Fach Mathematik