Gleichsetzungsverfahren in Mathe: Erklärung und Beispiele

Entdecke, wie du mit dem GleichsetzungsvLernen zwei unbekannte Variablen löst. Anhand von klaren Schritten und Beispielen wirst du das VLernen verstehen. Interessiert? Dies und vieles mehr findest du im folgenden Text!

Inhaltsverzeichnis zum Thema Gleichsetzungsverfahren

Das Quiz zum Thema: Gleichsetzungsverfahren

Was ist das Gleichsetzungsverfahren?

Frage 1 von 5

Wie viele Schritte umfasst das Gleichsetzungsverfahren?

Frage 2 von 5

Wann setzt man das Gleichsetzungsverfahren ein?

Frage 3 von 5

Was ist der Unterschied zwischen dem Einsetzungsverfahren und dem Gleichsetzungsverfahren?

Frage 4 von 5

Wie funktioniert das Gleichsetzungsverfahren?

Frage 5 von 5

Das Gleichsetzungsverfahren im Überblick

  • Das Gleichsetzungsverfahren ist ein Verfahren zum Lösen linearer Gleichungssysteme.
  • Beim Gleichsetzungsverfahren werden Seiten von zwei Gleichungen einander gleichgesetzt.
  • Besonders geeignet ist das Gleichsetzungsverfahren, wenn zwei Gleichungen bereits nach derselben Variable aufgelöst sind.
Gleichsetzungsverfahren: Lernvideo

Quelle sofatutor.com

Lineare Gleichungssysteme – Gleichsetzungsverfahren

Es gibt in Mathe verschiedene Verfahren zur Lösung linearer Gleichungssysteme (kurz LGS): das Gleichsetzungsverfahren, das Additionsverfahren und das Einsetzungsverfahren. 

Wir wollen hier das Gleichsetzungsverfahren für Gleichungssysteme mit zwei Variablen genauer betrachten. Dazu werden zunächst die Schritte des Gleichsetzungsverfahrens einfach erklärt und dann auf Beispiele angewendet.

Gleichsetzungsverfahren – Erklärung

Um ein Gleichungssystem aus zwei Gleichungen und zwei Unbekannten (Variablen) mit dem Gleichsetzungsverfahren zu lösen, gehen wir folgendermaßen vor:

  1. Beide Gleichungen werden nach derselben Variable aufgelöst. 
  2. Eine neue Gleichung mit nur einer Variablen wird formuliert, indem die beiden ungleichen Seiten der Gleichungen einander gleichgesetzt werden.
  3. Die neue Gleichung wird nach der verbleibenden Variable aufgelöst.
  4. Die berechnete Lösung der Variable wird in eine der beiden ursprünglichen Gleichungen eingesetzt, um die Lösung der zweiten Variable zu bestimmen.

Hinweis: Der erste Schritt kann übersprungen werden, wenn das Gleichungssystem bereits in einer entsprechenden Form vorliegt. 

Betrachten wir die Schritte einmal an einem beispielhaften Gleichungssystem:

\begin{array}{rrcrcr} \text{I}: & a & = & b & + & 3 \\ \text{II}: & -2a & = & 4b & & \end{array}

  1. Wir teilen die zweite Gleichung durch 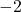-2, um auch hier die Form a = \dots zu erhalten:
    \begin{array}{rcrl} -2a & = & 4b & \vert :(-2) \\ a & = & -2b & \end{array}
  2. Wir setzen die rechten Seiten gleich:
    b + 3 = - 2b 
  3. Wir lösen nach 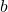b auf:
    \begin{array}{rcrl} b + 3 & = & -2b & \vert -b \\ 3 & = & -3b & \vert :(-3) \\ -1 & = & b & \end{array}
  4. Wir setzen 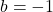b = -1 in die Gleichung a = -2b ein:
    a = -2 \cdot (-1) = 2

Die Lösung des Gleichungssystems lautet:
\begin{array}{rcr} a & = & 2 \\ b & = & -1 \end{array}

Gleichsetzungsverfahren – Probe

Mit der Probe können wir überprüfen, ob die mit dem Gleichsetzungsverfahren bestimmte Lösung für das Gleichungssystem richtig ist. Dazu werden die für die Variablen berechneten Werte in eine der Ausgangsgleichungen eingesetzt. Ergibt sich dabei eine falsche Aussage, dann ist bei der Berechnung ein Fehler passiert und wir müssen diese erneut prüfen.

Wir setzen in unserem Beispiel von eben für die Probe a = 2 und b = -1 in die erste Gleichung a = b + 3 ein:

\begin{array}{rcc} 2 & = & -1 + 3 \\ 2 & = & 2 \end{array}

Wir erhalten die wahre Aussage 2 = 2 und können somit davon ausgehen, dass wir richtig gerechnet haben.

Gleichsetzungsverfahren – Anwendung

Generell ist eine Anwendung des Gleichsetzungsverfahrens zum Lösen beliebiger linearer Gleichungssysteme mit zwei Variablen möglich. Besonders geeignet ist das Gleichsetzungsverfahren dabei in Fällen, bei denen der erste Schritt, beide Gleichungen nach derselben Variable aufzulösen, wenig aufwändig ist oder sogar übersprungen werden kann. 

Häufig hilft das Aufstellen eines linearen Gleichungssystems zum Beispiel bei der Bearbeitung von Textaufgaben, die so mit dem Gleichsetzungsverfahren gelöst werden können. Auch in der analytischen Geometrie treten beim Rechnen mit Vektoren lineare Gleichungssysteme auf, deren Lösung über das Gleichsetzungsverfahren möglich ist. Zum Beispiel wenn der Schnittpunkt zweier Geraden im Raum durch Gleichsetzen der Geradengleichungen ermittelt wird.

Gleichsetzungsverfahren – Beispiele

Beim Lösen von linearen Gleichungssystemen können verschiedene Fälle auftreten. Diese Fälle schauen wir uns im Folgenden an. Dabei lösen wir die Gleichungssysteme jeweils mit dem Gleichsetzungsverfahren.

Gleichsetzungsverfahren Anzahl der Lösungen

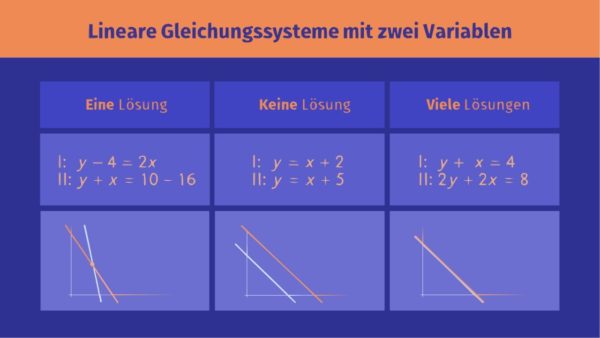
Die Abbildung zeigt drei Gleichungssysteme, die unterschiedlich viele Lösungen aufweisen. Das erkennst du hier bereits an der Darstellung der Gleichungen als Geraden im Koordinatensystem. Wir wollen die Gleichungssysteme nun mit dem Gleichsetzungsverfahren lösen, um zu sehen, wie wir die verschiedenen Fälle dabei erkennen.

  • Eine Lösung:
    \begin{array}{rccrcrcr} \text{I}: & y & - & 4 & = & 2x & & \\ \text{II}: & y & + & x & = & 10 & - & 16 \end{array}
    Wir lösen beide Gleichungen nach y auf:
    \begin{array}{rccrcr} \text{I}: & y & = & 2x & + & 4 \\ \text{II}: & y & = & -x & - & 6 \end{array}
    Und setzen dann die rechten Seiten gleich:
    \begin{array}{cccl} 2x + 4 & = & -x - 6 & \vert +x \\ 3x + 4 & = & -6 & \vert -4 \\ 3x & = & -10 & \vert : 3 \\ x & = & -\frac{10}{3} \end{array}
    Zuletzt setzen wir x = -\frac{10}{3} in die Gleichung y = -x - 6 ein:
    y = -(-\frac{10}{3}) - 6 = \frac{10}{3} - 6 = -\frac{8}{3}
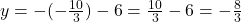
    Wir erhalten eine Lösung, die auch als Schnittpunkt von zwei Geraden interpretiert werden kann:
    \begin{array}{rcr} x & = & -\frac{10}{3} \\ y & = & -\frac{8}{3} \end{array}
  • Keine Lösung:
    \begin{array}{rccrcr} \text{I}: & y & = & x & + & 2 \\ \text{II}: & y & = & x & + & 5 \end{array}
    Beide Gleichungen sind bereits nach y aufgelöst. Wir setzen die rechten Seiten gleich:
    \begin{array}{cccl} x + 2 & = & x + 5 & \vert -x \\ 4 & = & 5 & \end{array}
    Wir erhalten eine falsche Aussage, damit hat das Gleichungssystem keine Lösung.
  • Unendlich viele Lösungen:
    \begin{array}{rrcrcr} \text{I}: & y & + & x & = & 4 \\ \text{II}: & 2y & + & 2x & = & 8 \end{array}
    Wir lösen beide Gleichungen nach x auf:
    \begin{array}{rrcrcr} \text{I}: & x & = & -y & + & 4 \\ \text{II}: & x & = & -y & + & 4 \end{array}
    Ein Gleichsetzen der rechten Seiten liefert:
    \begin{array}{cccl} -y + 4 & = & -y + 4 & \vert +y \\ 4 & = & 4 & \end{array}
    Wir erhalten eine wahre Aussage, die keine der Variablen enthält, damit hat das Gleichungssystem unendlich viele Lösungen in Form einer Geraden.

Häufig gestellte Fragen zum Gleichsetzungsverfahren

Das Gleichsetzungsverfahren ist ein mathematisches Verfahren zur Lösung von linearen Gleichungssystemen.

Das Gleichsetzungsverfahren besteht aus vier Schritten:

  • Auflösen beider Gleichungen nach eine Variablen
  • Gleichsetzen
  • Berechnung der verbleibenden Variable
  • Einsetzen der Variable in eine der ursprünglichen Gleichungen

Das Gleichsetzungsverfahren wird zur Lösung linearer Gleichungssysteme mit zwei Gleichungen und zwei Unbekannten eingesetzt.

Das Gleichsetzungsverfahren liefert bei Gleichungssystemen, die bereits in der geeigneten Form vorliegen, eine besonders schnelle Lösung, die mit wenig Rechenaufwand verbunden ist.

Das Gleichsetzungsverfahren eignet sich besonders für lineare Gleichungssysteme, bei denen die Gleichungen bereits nach derselben Variable aufgelöst sind oder die mit wenigen Umformungsschritten in diese Form gebracht werden können.

Beim Einsetzungsverfahren wird eine Gleichung nach einer Variablen aufgelöst und für diese in die andere Gleichung eingesetzt. 
Beim Gleichsetzungsverfahren werden beide Gleichungen nach derselben Variablen aufgelöst und die anderen Seiten der beiden Gleichungen dann gleichgesetzt.

Das Gleichsetzungsverfahren beschreibt allgemein ein Vorgehen zur Lösung von linearen Gleichungssystemen. Bei der Anwendung gibt es die beiden Möglichkeiten, beide Gleichungen nach der einen oder der anderen Variablen aufzulösen. Dabei bietet sich in der Regel diejenige Variable an, bei der weniger Umformungsschritte benötigt werden.

Super! Das Thema: kannst du schon! Teile deine Learnings und Fragen mit der Community!

Alle Artikel aus dem Fach Mathematik