Bogenmaß und Gradmaß – Bedeutung, Umrechnung und Beispiele

Erfahre, dass ein Vollwinkel sowohl  im Bogenmaß als auch im Gradmaß entspricht. Entdecke die Definitionen, die Umrechnung zwischen den Maßen und Beispiele für verschiedene Winkel.

Inhaltsverzeichnis zum Thema Bogenmaß und Gradmaß

Das Quiz zum Thema: Bogenmaß & Gradmaß

Was ist das Bogenmaß eines Winkels?

Frage 1 von 5

Wie wird Gradmaß in Bogenmaß umgerechnet?

Frage 2 von 5

Wann wird das Gradmaß verwendet?

Frage 3 von 5

Wie rechnet man ein Gradmaß in Bogenmaß um?

Frage 4 von 5

Was ist der Unterschied zwischen Bogenmaß und Gradmaß?

Frage 5 von 5

Bogenmaß und Gradmaß im Überblick

  • Bogenmaß und Gradmaß sind Einheiten für die Größe eines Winkels.

  • Ein ganzer Kreis (Vollwinkel) entspricht 360^\circ im Gradmaß und 2\pi im Bogenmaß.

  • Das Bogenmaß leitet sich aus der Bogenlänge am Einheitskreis ab und wird bevorzugt im Zusammenhang mit den trigonometrischen Funktionen verwendet.

Bogenmaß und Gradmaß Video

Quelle sofatutor.com

Bildergalerie zum Thema Bogenmaß & Gradmaß

Bogenmaß und Gradmaß
Bogenmaß und Gradmaß
Bogenmaß und GradmaßWas ist Gradmaß?Was ist BogenmaßWas ist BogenmaßBogenmaß und Gradmaß VergleichBogenmaß und Gradmaß UmrechnungBogenmaß und Gradmaß - RAD und DEGBogenmass und Gradmass Umrechnung

Bogenmaß und Gradmaß einfach erklärt   

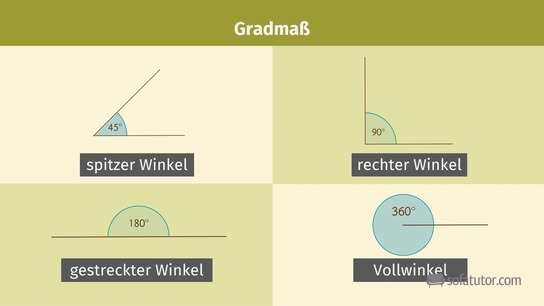
In Mathe können Winkelmaße im Gradmaß und im Bogenmaß angegeben werden.
Das Gradmaß eines Winkels bezieht sich auf den Vollwinkel von 360^\circ, der einem ganzen Kreis entspricht. Das Bogenmaß beschreibt den Mittelpunktswinkel am Einheitskreis durch die Länge des Bogens, den das Kreissegment hat. Da der Einheitskreis den Radius r = 1 hat, ist sein Umfang die Länge: 2r\pi = 2 \cdot 1 \cdot \pi = 2\pi. Dies entspricht dem Vollwinkel im Bogenmaß. Es gilt der Zusammenhang:
\dfrac{\alpha}{360^\circ} = \dfrac{b}{2\pi}

Hierbei bezeichnet \alpha den Mittelpunktswinkel und b die Bogenlänge des Kreissegments.

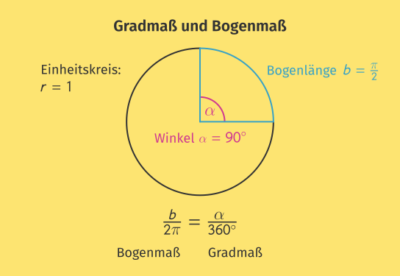
In der Abbildung siehst du beide Angaben bezogen auf einen Viertelkreis. Für das Gradmaß ergibt sich:
\alpha = 360^\circ : 4 = 90^\circ

Im Bogenmaß erhalten wir:
b = 2\pi : 4 = \frac{\pi}{2}

Gradmaß und Bogenmaß einfach erklärt

Bogenmaß eines Winkels – Definition

Das Bogenmaß eines Winkels \alpha gibt die Bogenlänge eines Kreissegments, mit Mittelpunktswinkel \alpha, im Einheitskreis an.

Gradmaß eines Winkels – Definition

Das Gradmaß eines Winkels \alpha gibt an, welchen Anteil eines Vollwinkels er überstreicht. Ein ganzer Kreis entspricht dabei einem Winkel von 360^\circ.

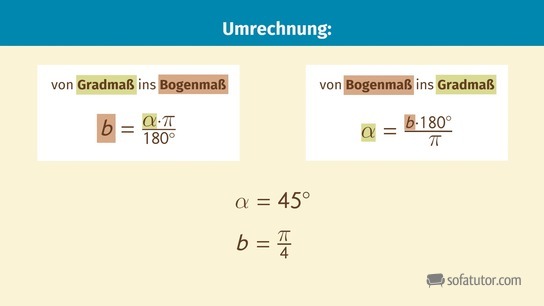
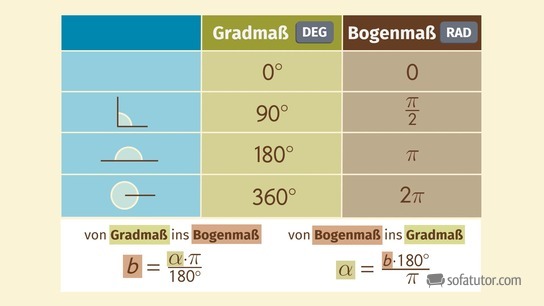
Umrechnung zwischen Winkelmaßen

Durch Umstellen des allgemeinen Zusammenhangs
\dfrac{\alpha}{360^\circ} = \dfrac{b}{2\pi}
können wir Winkel vom Gradmaß ins Bogenmaß und umgekehrt umwandeln.

Gradmaß in Bogenmaß umrechnen

Das Maß eines Winkels \alpha im Gradmaß können wir im Bogenmaß mit folgender Formel berechnen:

b = \dfrac{\alpha}{360^\circ} \cdot 2\pi

Dazu haben wir den allgemeinen Zusammenhang der Einheiten mit 2\pi multipliziert. Du kannst die Formel noch vereinfachen, indem du mit 2 kürzt:

b = \dfrac{\alpha}{180^\circ} \cdot \pi

So ergibt sich für einen Winkel von \alpha = 120^\circ (Gradmaß) der entsprechende Winkel b im Bogenmaß:

b = \dfrac{120^\circ}{180^\circ} \cdot \pi = \dfrac{2}{3}\pi \approx 2,09

Bogenmaß in Gradmaß umrechnen

Das Maß eines Winkels b im Bogenmaß können wir mit folgender Formel in Gradzahlen umrechnen:

\alpha = \dfrac{b}{2\pi} \cdot 360^\circ

Dazu haben wir den allgemeinen Zusammenhang der Einheiten mit 360^\circ multipliziert. Du kannst die Formel noch vereinfachen, indem du mit 2 kürzt:

\alpha = \dfrac{b}{\pi} \cdot 180^\circ

So ergibt sich für einen Winkel von b =\dfrac{2}{3}\pi (Bogenmaß) der entsprechende Winkel \alpha im Gradmaß:

\alpha = \dfrac{\frac{2}{3}\pi}{\pi} \cdot 180^\circ = \frac{2}{3} \cdot 180^\circ = 120^\circ

Beispiele für Winkel im Bogen- und Gradmaß

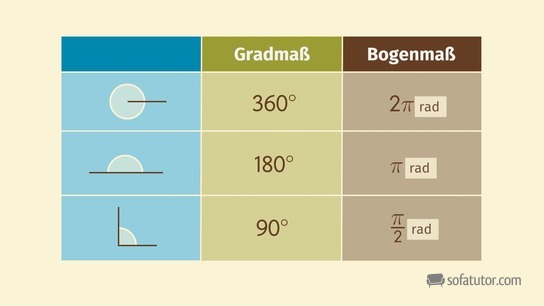
In der Tabelle siehst du wichtige Winkel im Gradmaß und im Bogenmaß zusammengefasst:

Gradmaß \alpha Bogenmaß b Anteil Kreis
0^\circ 0 –
45^\circ \frac{\pi}{4} \frac{1}{8}
60^\circ \frac{\pi}{3} \frac{1}{6}
90^\circ \frac{\pi}{2} \frac{1}{4}
180^\circ \pi \frac{1}{2}
360^\circ 2\pi 1

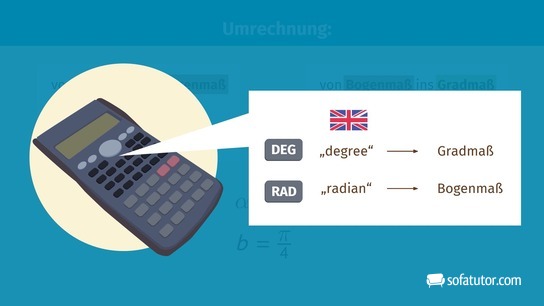
Bogenmaß und Gradmaß am Taschenrechner

Bei deinem Taschenrechner kannst du einstellen, ob du Winkel im Gradmaß oder im Bogenmaß verwendest. Die aktuelle Einstellung erkennst du in der Regel an einem kleinen D oder R oben im Display. Dabei steht D für das Gradmaß: englisch degree, kurz DEG. Der Buchstabe R steht für das Bogenmaß: englisch radiant, kurz RAD.
Es empfiehlt sich, die Einstellung der Taschenrechners bei der Verwendung von Winkeln immer einmal kurz zu überprüfen und wenn nötig entsprechend anzupassen.
Eine Umrechnung eines Winkelmaßes von Grad in Rad und umgekehrt kannst du mit den bekannten Formeln vornehmen.  

Häufig gestellte Fragen zum Thema Gradmaß und Bogenmaß

Das Bogenmaß ist eine Einheit für Winkel. Die Größe des Winkels wird dabei über die Bogenlänge eines Kreissektors mit entsprechendem Mittelpunktswinkel am Einheitskreis beschrieben.

Jeder Winkel kann sowohl im Grad- als auch im Bogenmaß angegeben werden. Bei geometrischen Überlegungen wird meist das Gradmaß verwendet. Im Zusammenhang mit den trigonometrischen Funktionen findet häufig das Bogenmaß Anwendung.

Das Bogenmaß eines Winkels ist definiert als die Länge des Kreisbogens am Einheitskreis.

Die Berechnung eines Winkels im Bogenmaß erfolgt über die Formel:
b = \dfrac{\alpha}{180^\circ} \cdot \pi

Unterschied Bogenmaß und Gradmaß: Das Gradmaß beschreibt die Größe eines Winkels als Anteil am Vollwinkel 360^\circ. Beim Bogenmaß wird der Winkel durch die korrespondierende Bogenlänge eines Kreissegments im Einheitskreis beschrieben.  

Das Bogenmaß wird häufig im Zusammenhang mit den trigonometrischen Funktionen, zum Beispiel \sin x und \cos x, verwendet.

Um im Taschenrechner mit dem Bogenmaß zu rechnen, sollte dieser auf RAD eingestellt sein. Das erkennst du meist an einem kleinen R oben im Display, ein D steht hier für das Gradmaß, kurz DEG.

Das Gradmaß beschreibt einen Winkel über den Anteil des Vollwinkels 360^\circ, den dieser überstreicht.

Aus dem Bogenmaß b kann das Gradmaß eines Winkels mit der folgenden Formel berechnet werden:
\alpha = \dfrac{b}{\pi} \cdot 180^\circ

Für die geometrische Betrachtung von Winkeln werden diese zumeist im Gradmaß angegeben.

Ein Winkel von 20^\circ überstreicht \frac{1}{18} des Vollwinkels 360^\circ, er entspricht also \frac{1}{18} eines Kreises.
Im Bogenmaß hat er einen Wert von:
b = \dfrac{20^\circ}{180^\circ} \cdot \pi = \frac{\pi}{9}

Ein Winkel von 45^\circ entspricht \frac{1}{8} des Vollwinkels 360^\circ. Das bedeutet, er entspricht \frac{1}{8} des Kreises.
Im Bogenmaß hat er einen Wert von:
b = \dfrac{45^\circ}{180^\circ} \cdot \pi = \frac{\pi}{2}

Ein Winkel im Gradmaß erhält man als entsprechenden Anteil des Vollwinkels 360^\circ.
Zum Beispiel entspricht ein halber Kreis einem Winkel von 360^\circ : 2 = 180^\circ.

Rad oder Radiant ist ein anderer Begriff für das Bogenmaß. Ein Winkel \alpha im Gradmaß kann mit folgender Formel in das Bogenmaß umgerechnet werden:
b = \dfrac{\alpha}{180^\circ} \cdot \pi

Super! Das Thema: kannst du schon! Teile deine Learnings und Fragen mit der Community!

Alle Artikel aus dem Fach Mathematik