Funktionsgraphen – Eigenschaften, Erklärung und Beispiele
Lerne, wie Funktionsgraphen Funktionen im Koordinatensystem darstellen. Lerne, Funktionsgraphen zu zeichnen, wichtige Punkte zu identifizieren, Transformationen durchzuführen und verschiedene Funktionstypen zu erkennen. Interessiert? Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Funktionsgraphen
Funktionsgraphen – Definition
Eine Funktion ![]() ordnet jedem
ordnet jedem ![]() aus dem Definitionsbereich genau ein
aus dem Definitionsbereich genau ein ![]() aus dem Wertebereich zu. Jedoch kann ein
aus dem Wertebereich zu. Jedoch kann ein ![]() -Wert zu mehreren
-Wert zu mehreren ![]() -Werten gehören, wie wir gleich sehen werden.
-Werten gehören, wie wir gleich sehen werden.
Ein Funktionsgraph, kurz Graph, ist nun die Menge aller dieser Wertepaare ![]() , die in einem Koordinatensystem dargestellt werden. Er ist also eine bildliche Darstellung der Funktion.
, die in einem Koordinatensystem dargestellt werden. Er ist also eine bildliche Darstellung der Funktion.
Funktionsgraphen zeichnen
Um den Graphen einer Funktion ![]() zu bestimmen, befolgst du folgende Schritte:
zu bestimmen, befolgst du folgende Schritte:
- Eine Wertetabelle erstellen, in die du für verschiedene
 -Werte den zugehörigen Wert
-Werte den zugehörigen Wert  -Wert einträgst. Dazu setzt du einen
-Wert einträgst. Dazu setzt du einen  -Wert in
-Wert in 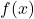 ein und schreibst das Ergebnis zu
ein und schreibst das Ergebnis zu  .
.
Merke: Je mehr Punkte du verwendest, desto genauer wird der Graph. - Nun hast du einige Punkte
 , die du im Koordinatensystem markierst.
, die du im Koordinatensystem markierst. - Den Verlauf des Graphen kannst du skizzieren, indem du die Punkte zu einer Geraden oder Kurve verbindest.
Funktionsgraph zeichnen – Beispiel lineare Funktion
Eine lineare Funktion kann geschrieben werden als:
![]()
Dabei steht ![]() für die Steigung und
für die Steigung und ![]() wird als
wird als ![]() -Achsenabschnitt bezeichnet.
-Achsenabschnitt bezeichnet.
Die Steigung zeigt an, wie stark ein Graph steigt bzw. fällt. Der ![]() -Achsenabschnitt ist der Punkt, an dem der Graph die
-Achsenabschnitt ist der Punkt, an dem der Graph die ![]() -Achse schneidet:
-Achse schneidet:
![]()
Der Funktionsgraph einer linearen Funktion zeigt eine Gerade.

Schauen wir uns die einfache lineare Funktion ![]() an.
an.
Die Wertetabelle hierzu sieht wie folgt aus:
Trägst du diese Werte in ein Koordinatensystem ein, erhältst du den zugehörigen Graphen. Bei einer linearen Funktion reichen zwei Punkte aus, die zu einer Gerade verbunden werden.
Statt eine Wertetabelle zu nutzen, kann der Graph der linearen Funktion auch mithilfe des ![]() -Achsenabschnitts und eines Steigungsdreiecks gezeichnet werden.
-Achsenabschnitts und eines Steigungsdreiecks gezeichnet werden.
Dazu wird die Steigung als Bruch dargestellt: ![]() . Ausgehend von einem beliebigen Punkt der Geraden, zum Beispiel dem
. Ausgehend von einem beliebigen Punkt der Geraden, zum Beispiel dem ![]() -Achsenabschnitt, gehst du dann
-Achsenabschnitt, gehst du dann ![]() Einheiten in
Einheiten in ![]() -Richtung und
-Richtung und ![]() Einheiten in
Einheiten in ![]() -Richtung und erhältst so einen weiteren Punkt, durch den die Gerade verläuft.
-Richtung und erhältst so einen weiteren Punkt, durch den die Gerade verläuft.
Um den Funktionsgraphen einer linearen Funktion zu beschreiben, brauchst du also eine Wertetabelle oder markante Werte, wie den ![]() -Achsenabschnitt und die Steigung.
-Achsenabschnitt und die Steigung.
Für Funktionen höherer Potenzen sind weitere charakteristische Punkte nötig.
Charakteristische Punkte eines Funktionsgraphen
Wichtige Punkte, die den Graphen einer Funktion charakterisieren, sind: Hochpunkte, Tiefpunkte, Wendepunkte und Schnittpunkte des Funktionsgraphen mit den Koordinatenachsen.
Hoch- bzw. Tiefpunkte werden auch Extrempunkte genannt. Folgende Bedingungen müssen gelten:
 (die Steigung an dieser Stelle ist null)
(die Steigung an dieser Stelle ist null)  notwendige Bedingung
notwendige Bedingung (zweite Ableitung an diesem Punkt ist ungleich null)
(zweite Ableitung an diesem Punkt ist ungleich null)  hinreichende Bedingung
hinreichende Bedingung
Beispiel: Die quadratische Funktion ![]() auf dem oberen Bild hat einen Tiefpunkt an der Stelle
auf dem oberen Bild hat einen Tiefpunkt an der Stelle ![]() . Die quadratische Funktion
. Die quadratische Funktion ![]() auf dem unteren Bild hingegen hat an dieser Stelle einen Hochpunkt.
auf dem unteren Bild hingegen hat an dieser Stelle einen Hochpunkt.

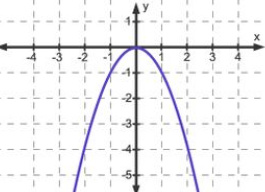
Zwischen einem Hoch- und Tiefpunkt bzw. umgekehrt kann ein Wende- oder Sattelpunkt liegen. Für den Wendepunkt gilt:
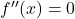 (zweite Ableitung an diesem Punkt ist null)
(zweite Ableitung an diesem Punkt ist null)
 notwendige Bedingung
notwendige Bedingung
 hinreichende Bedingung
hinreichende Bedingung
Für den Sattelpunkt gilt zusätzlich, dass die Steigung an diesem Punkt null sein muss:
![]()
Beispiele:
Im folgenden Bild sehen wir einen Graphen mit einer Wendestelle im Punkt ![]() :
:

Die kubische Funktion ![]() hat einen Sattelpunkt bei
hat einen Sattelpunkt bei ![]() :
:

Für die Schnittpunkte mit den Koordinatenachsen gilt:
- Der
 -Achsenabschnitt ist der Schnittpunkt mit der
-Achsenabschnitt ist der Schnittpunkt mit der  -Achse. Er liegt bei
-Achse. Er liegt bei  .
. - Die Nullstellen sind die Schnittpunkte mit der
 -Achse. Sie werden als Lösungen
-Achse. Sie werden als Lösungen  der Gleichung
der Gleichung  bestimmt. Die Nullstellen haben dann die Koordianten
bestimmt. Die Nullstellen haben dann die Koordianten 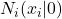
Beispiel:
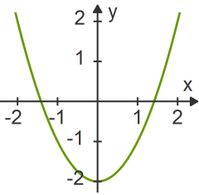
Folgende Parabel schneidet die ![]() -Achse bei
-Achse bei ![]() . Außerdem hat der Graph Nullstellen, also Schnittpunkte mit der
. Außerdem hat der Graph Nullstellen, also Schnittpunkte mit der ![]() -Achse, bei
-Achse, bei ![]() und
und ![]() :
:
Symmetrie von Funktionsgraphen
Es gibt Achsensymmetrie und Punktsymmetrie. Achsensymmetrie/Punktsymmetrie bedeutet, dass bei der Spiegelung von Funktionsgraphen an bestimmten Achsen/Punkten der gleiche Graph resultiert. Häufig ist damit die ![]() -Achse bzw. der Ursprung gemeint.
-Achse bzw. der Ursprung gemeint.
Die Punktsymmetrie zum Ursprung prüfst du mit folgender Bedingung:
![]()
Ein Beispiel hierfür ist die Funktion ![]() , die wir oben betrachtet haben.
, die wir oben betrachtet haben.
Setzt du ![]() in
in ![]() ein, erhältst du:
ein, erhältst du:
![]()
Achsensymmetrie zur ![]() -Achse ist gegeben, wenn gilt:
-Achse ist gegeben, wenn gilt:
![]()
Dies ist der Fall bei der quadratischen Funktion ![]() . Setze
. Setze ![]() ein:
ein:
![]()
Transformation von Funktionsgraphen
Du kannst Funktionsgraphen in ![]() – oder
– oder ![]() -Richtung verschieben, strecken, stauchen oder spiegeln. Wir betrachten im Folgenden, wie sich diese Transformationen auf den Funktionsterm auswirken.
-Richtung verschieben, strecken, stauchen oder spiegeln. Wir betrachten im Folgenden, wie sich diese Transformationen auf den Funktionsterm auswirken.
Verschieben entlang der ![]() -Achse:
-Achse:
Um einen Graphen entlang der ![]() -Achse zu verschieben, wird eine Konstante
-Achse zu verschieben, wird eine Konstante ![]() zu
zu ![]() addiert:
addiert:
![]()
Dabei gilt:
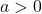 : Der Graph ist um
: Der Graph ist um  Einheiten nach links verschoben.
Einheiten nach links verschoben.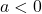 : Der Graph ist um
: Der Graph ist um  Einheiten nach rechts verschoben.
Einheiten nach rechts verschoben.
Verschieben entlang der ![]() -Achse:
-Achse:
Eine Verschiebung entlang der ![]() -Achse nach oben oder unten erhalten wir, indem wir eine Konstante
-Achse nach oben oder unten erhalten wir, indem wir eine Konstante ![]() zum Funktionsterm von
zum Funktionsterm von ![]() addieren:
addieren:
![]()
Dabei gilt:
 : Der Graph ist um
: Der Graph ist um 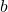 Einheiten nach oben verschoben.
Einheiten nach oben verschoben. : Der Graph ist um
: Der Graph ist um 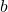 Einheiten nach unten verschoben.
Einheiten nach unten verschoben.
Stauchung/Streckung in ![]() -Richtung:
-Richtung:
Um den Graphen in ![]() -Richtung zu stauchen oder zu strecken, wird die Variable
-Richtung zu stauchen oder zu strecken, wird die Variable ![]() mit einem Faktor
mit einem Faktor ![]() multipliziert:
multipliziert:
![]()
Dabei gilt:
 Der Graph ist in
Der Graph ist in  -Richtung gestreckt.
-Richtung gestreckt. : Der Graph ist in
: Der Graph ist in  -Richtung gestaucht.
-Richtung gestaucht.
Stauchung/Streckung in ![]() -Richtung:
-Richtung:
Um den Graphen in ![]() -Richtung zu stauchen oder zu strecken, wird ein Faktor
-Richtung zu stauchen oder zu strecken, wird ein Faktor ![]() mit dem Funktionsterm von
mit dem Funktionsterm von ![]() multipliziert:
multipliziert:
![]()
Dabei gilt:
 Der Graph ist in
Der Graph ist in  -Richtung gestaucht.
-Richtung gestaucht. : Der Graph ist in
: Der Graph ist in  -Richtung gestreckt.
-Richtung gestreckt.
Spiegelung:
Häufig werden Graphen an der ![]() – bzw.
– bzw. ![]() -Achse oder am Ursprung des Koordinatensystems gespiegelt. Es gelten folgende Bedingungen:
-Achse oder am Ursprung des Koordinatensystems gespiegelt. Es gelten folgende Bedingungen:
- Spiegelung an der
 -Achse:
-Achse: 
- Spiegelung an der
 -Achse:
-Achse: 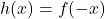
- Spiegelung am Ursprung
 :
: 
Transformation am Beispiel der Parabel

- Im ersten Bild oben rechts wird
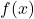 um eins nach oben geschoben, indem
um eins nach oben geschoben, indem 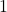 addiert wird. Der zugehörige Funktionsterm ist
addiert wird. Der zugehörige Funktionsterm ist  .
. - Im nächsten Bild wird
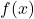 um
um 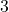 Einheiten nach unten verschoben. Der zugehörige Funktionsterm ist
Einheiten nach unten verschoben. Der zugehörige Funktionsterm ist 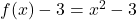 .
. - Der dritte Graph von oben ist um eine Einheit nach rechts verschoben. Hier lautet der Funktionsterm
 .
. - In der letzten Abbildung erkennen wir eine Verschiebung um zwei Einheiten nach links. Damit ist der Funktionsterm
 .
.
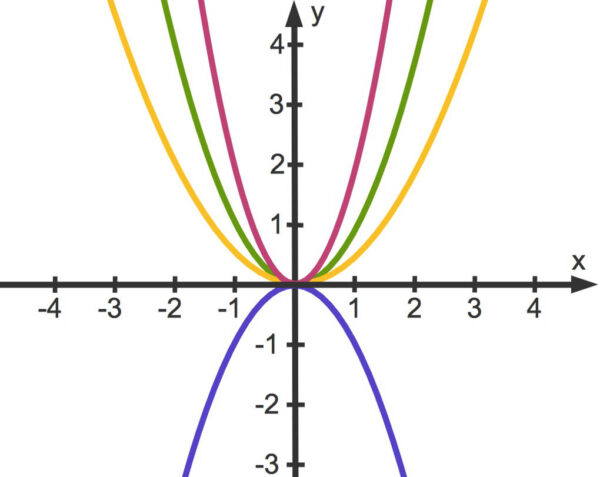
Im oben stehenden Bild sehen wir die Normalparabel in Grün, eine gestreckte Parabel in Rot und eine gestauchte Parabel in Gelb. Die blaue Parabel wurde an der ![]() -Achse gespiegelt.
-Achse gespiegelt.
Funktionstypen – Beispiele
Wir haben im obigen Text schon verschiedene Funktionsgraphen und Funktionstypen kennengelernt. Es gibt noch mehr Arten von Funktionen. Die folgende Übersicht zeigt dir einige davon:
| Art der Funktion | Beispiel |
|---|---|
| lineare Funktion (Gerade) | |
| quadratische Funktion (Parabel) | |
| Potenzfunktion | |
| Wurzelfunktion | |
| Exponentialfunktion | |
| trigonometrische Funktion | |
| …. |
Funktionsgraphen erkennen
Wir können Funktionsgraphen anhand der Wertetabelle erkennen. Dies schauen wir uns anhand linearer und quadratischer Funktionen an:
Lineare Funktionen:
Erhöhst du den ![]() -Wert um eine Einheit, erhöht sich der
-Wert um eine Einheit, erhöht sich der ![]() -Wert immer um eine feste Konstante:
-Wert immer um eine feste Konstante:
| x | y |
|---|---|
Wenn sich ![]() um eins erhöht, erhöht sich
um eins erhöht, erhöht sich ![]() immer um die Konstante
immer um die Konstante ![]() .
.
Quadratische Funktionen:
Hier muss zunächst die Differenzendifferenz berechnet werden. Das bedeutet, wir berechnen die Differenz der ersten beiden ![]() -Werte und die Differenz des dritten und zweiten
-Werte und die Differenz des dritten und zweiten ![]() -Werts. Ist die Differenz zwischen diesen beiden Differenzen konstant, handelt es sich um eine quadratische Funktion. Wir betrachten hierzu ein Beispiel:
-Werts. Ist die Differenz zwischen diesen beiden Differenzen konstant, handelt es sich um eine quadratische Funktion. Wir betrachten hierzu ein Beispiel:
| x | y |
|---|---|
Die Differenz der ersten beiden ![]() -Werte ist:
-Werte ist: ![]() .
.
Die Differenz des zweiten und dritten ![]() -Werts ist :
-Werts ist : ![]() .
.
Die Differenz dieser beiden Differenzen ist: ![]()
Die Veränderung des ![]() -Werts erhöht sich also immer um
-Werts erhöht sich also immer um ![]() :
:
Von ![]() zu
zu ![]() ist die Veränderung
ist die Veränderung ![]() .
.
Von ![]() zu
zu ![]() ist die Veränderung
ist die Veränderung ![]() .
.
Von ![]() zu
zu ![]() ist sie:
ist sie: ![]() etc.
etc.
Exkurs – Flächen zwischen Funktionsgraphen
Eine weitere Aufgabe, die häufig gestellt wird, ist die Berechnung der Fläche zwischen zwei Funktionsgraphen, beispielsweise ![]() und
und ![]() .
.
Dazu berechnest du die Differenzfunktion ![]() .
.
Um die Fläche unter dieser Differenzfunktion zu berechnen, sind zunächst die Nullstellen zu bestimmen. Sind lediglich zwei Nullstellen vorhanden, bilden diese die Unter- und Obergrenze für das Integral (Flächenberechnung). Hast du mehr als zwei Nullstellen (und damit Schnittstellen zwischen ![]() und
und ![]() ), benötigst du Teilintegrale. Das erste Integral geht dann von der ersten zur zweiten Nullstelle, das zweite Teilintegral von der zweiten zur dritten Nullstelle etc. Beachte, dass die Integrale in Betragsstriche gesetzt werden müssen.
), benötigst du Teilintegrale. Das erste Integral geht dann von der ersten zur zweiten Nullstelle, das zweite Teilintegral von der zweiten zur dritten Nullstelle etc. Beachte, dass die Integrale in Betragsstriche gesetzt werden müssen.
Häufig gestellte Fragen zum Thema Funktionsgraphen

