Senkrecht – Erklärung und Beispiele

Erfahre, dass Senkrechte in der Mathematik Geraden sind, die sich im rechten Winkel schneiden. Entdecke Beispiele aus dem Alltag, lerne, wie man senkrechte Linien zeichnet und überprüft und erfahre mehr über ihre Anwendung im Koordinatensystem und im dreidimensionalen Raum. Dies und vieles mehr findest du im folgenden Text!

Inhaltsverzeichnis zum Thema Senkrecht

Senkrecht im Überblick

  • Der Begriff Senkrechte kommt in der Mathematik im Teilgebiet der Geometrie vor.

  • Senkrechte Geraden in der Ebene schneiden sich immer im rechten Winkel.

  • Im dreidimensionalen Raum gibt es auch Senkrechte, diese kannst du mit dem Skalarprodukt berechnen.

Senkrechte Linien: Lernvideo

Quelle sofatutor.com

Senkrechte Geraden – Definition

Zwei Geraden sind senkrecht zueinander, wenn sie sich im rechten Winkel (90^\circ-Winkel) schneiden.

Merke: Geraden sind gerade Linien, die keinen Anfangs- oder Endpunkt haben. Sie sind also unendlich lang in beide Richtungen fortführbar.

Wenn zwei Geraden senkrecht sind, kannst du das auch mit diesem Symbol darstellen: \perp
Die Geraden a und b im folgenden Bild sind senkrecht zueinander.

senkrechte Geraden

Das kannst du so angeben:
a \perp b

Senkrechte Linien im Alltag

Senkrechte Linien kommen auch häufig in der Natur oder im Alltag vor.

An Kreuzungen schneiden sich zwei Straßen häufig im rechten Winkel, damit sind es zwei senkrechte Geraden:

Senkrechte Straßen

Bei Hausdächern kannst du ebenfalls häufig senkrechte Linien erkennen:

Senkrechte Geraden am Hausdach

Auch viele Buchstaben enthalten senkrechte Linien, zum Beispiel diese:

H, E, F, L, T

Wenn du stehst, bildet dein Körper eine senkrechte Linie zur (idealisierten) Erdoberfläche:

Senkrechte Linien in der Natur

Senkrechte Linien zeichnen

Senkrechte Linien kannst du mit dem Geodreieck zeichnen. 

Dazu zeichnest du zunächst eine Gerade. Dann legst du die Mittellinie des Geodreiecks auf diese Gerade. Nun zeichnest du eine weitere Gerade entlang der längsten Seite des Geodreiecks.

Senkrechte Linien zeichnen

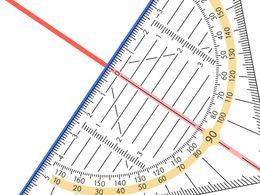
Senkrechte Linien überprüfen

Um zu überprüfen, ob zwei Geraden senkrecht zueinander stehen, kannst du ebenfalls das Geodreieck verwenden: 

Lege die Spitze des Geodreiecks im Winkel an. Verlaufen die Geraden genau an den beiden Seiten des Geodreiecks, dann sind sie senkrecht zueinander.

Es gibt noch einen anderen Weg, Geraden mit dem Geodreieck daraufhin zu überprüfen, ob sie senkrecht sind. Dazu legst du die Mittellinie des Geodreiecks auf die eine Gerade. Verläuft die andere Gerade genau entlang der längsten Seite des Geodreiecks, sind die beiden Geraden senkrecht zueinander.

Senkrechte Linien überprüfen

Senkrechte Geraden im Koordinatensystem

Zwei Geraden können im Koordinatensystem senkrecht zueinander stehen. Senkrechte Geraden kannst du mithilfe der Steigungen der Geraden berechnen. Dazu musst du dir Folgendes merken: Wenn die Steigungen multipliziert -1 ergeben, dann stehen die beiden Geraden senkrecht zueinander.

Berechne bei den folgenden beiden Geraden, ob diese senkrecht zueinander stehen:
a = - 3x + 2
b = \frac{1}{3}x + 3

Die Steigungen musst du miteinander multiplizieren: - 3 \cdot \frac{1}{3} = - 1
Das Produkt der Steigungen ist -1. Das bedeutet, die Geraden stehen senkrecht zueinander.

Es gibt auch senkrechte Geraden im Koordinatensystem, die die x-Achse im rechten Winkel schneiden. Senkrechte Schnittgeraden zur x-Achse werden auch vertikale Geraden genannt und verlaufen immer parallel zur y-Achse.
Im folgenden Bild siehst du eine senkrechte Gerade:

vertikale Gerade im Koordinatensystem

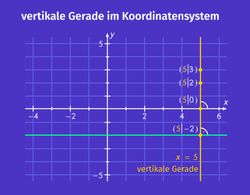
Senkrechte Geraden haben immer die Gleichung x = C , dabei ist C eine beliebige Konstante. Die senkrechte Gerade im Bild hat die Gleichung x = 5.

Im Koordinatensystem gibt es auch horizontale Geraden, die die y-Achse im rechten Winkel schneiden. Horizontale Schnittgeraden zur y-Achse werden auch waagrechte Geraden genannt und verlaufen immer parallel zur x-Achse.
Im folgenden Bild siehst du eine horizontale Gerade:

horizontale Gerade im Koordinatensystem

Waagerechte Geraden haben immer die Funktionsgleichung y = C, dabei ist C eine beliebige Konstante. Die Gerade im Bild hat die Gleichung y = - 2.

Merke: Horizontale Geraden werden auch waagerechte Geraden genannt.

Senkrechte im dreidimensionalen Raum

Um senkrechte Geraden im Raum zu ermitteln, benötigst du das Skalarprodukt der Richtungsvektoren. Das Skalarprodukt ist dabei die Summe der Zeilenprodukte. Ergibt das Skalarprodukt 0, dann stehen die beiden Geraden senkrecht zueinander.

Probiere es selbst aus: Überprüfe, ob die folgenden beiden Geraden a und b senkrecht zueinander stehen.
a=\begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix} + t \cdot \begin{pmatrix} 3 \\ 3 \\ 0 \end{pmatrix}
b=\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} - 3 \\ 3 \\ 0 \end{pmatrix}

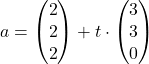
Du bildest das Skalarprodukt aus den beiden Richtungsvektoren der Geradengleichungen:
\begin{pmatrix} 3 \\ 3 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} - 3 \\ 3 \\ 0 \end{pmatrix} = 3 \cdot (- 3) + 3 \cdot 3 + 0 \cdot 0 = 0
Das Skalarprodukt ergibt 0, also stehen die Geraden a und b senkrecht zueinander.

Um senkrechte Ebenen im Raum zu ermitteln, benötigst du ebenfalls das Skalarprodukt. Wenn das Skalarprodukt ihrer Normalvektoren 0 ergibt, stehen die Ebenen senkrecht zueinander.

Probiere es selbst aus: Überprüfe, ob die folgenden beiden Ebenen senkrecht zueinander stehen.
E_1: -4x_1 + x_2 + 3x_3 - 3 = 0
E_2: x_1 + x_2 + x_3 - 6 = 0

Du bildest das Skalarprodukt aus den beiden Normalvektoren der Ebenengleichungen:
\begin{pmatrix} -4 \\ 1 \\ 3 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 1 \\ 3 \end{pmatrix} = (-4) \cdot 1 + 1 \cdot 1 + 3 \cdot 1 = 0
Das Skalarprodukt ergibt 0, also sind die Ebenen senkrecht zueinander.

Häufig gestellte Fragen zum Thema Senkrechte Linien

Zwei Geraden sind senkrecht zueinander, wenn sie sich im rechten Winkel schneiden. Auch im dreidimensionalen Raum können Geraden und Ebenen senkrecht zueinander stehen.

Mit Senkrechten werden senkrechte Linien bezeichnet, die sich im rechten Winkel schneiden.

Zwei gerade Linien, die sich im rechten Winkel schneiden, werden auch senkrechte Geraden genannt.

Senkrechte Strecken sind begrenzte Linien mit einem Start- und Endpunkt, die sich im rechten Winkel schneiden. Senkrechte Strahlen hingegen schneiden sich ebenfalls im rechten Winkel, haben aber nur einen Startpunkt und sind nicht von einem Endpunkt begrenzt.

Viele geometrische Körper haben senkrechte Kanten. Beim Würfel erkennst du beispielsweise, dass sich alle Kanten, die in den Ecken aufeinanderstoßen, im rechten Winkel schneiden:

Senkrechte Kanten beim Würfel

Im Alltag kommen senkrechte Linien häufig vor, zum Beispiel bei Straßenkreuzungen oder Hausdächern. Auch unsere Buchstaben enthalten oft senkrechte Linien. Auch in der Natur gibt es senkrechte Linien: Wenn du stehst, bildet dein Körper außerdem eine senkrechte Linie zur (idealisierten) Erdoberfläche.

Senkrechte Linien kannst du mit dem Geodreieck zeichnen. 

Zunächst zeichnest du eine Gerade. Danach legst du die Mittellinie des Geodreiecks auf diese Gerade. Nun zeichnest du eine weitere Gerade entlang der längsten Seite des Geodreiecks.

Senkrechte Geraden im Koordinatensystem kannst du mithilfe der Steigungen der Geraden berechnen. Wenn die Steigungen multipliziert -1 ergeben, dann stehen die beiden Geraden senkrecht zueinander.

Im zweidimensionalen Raum sind zwei Geraden senkrecht zueinander, wenn sie sich im rechten Winkel schneiden. Zwei Geraden sind stattdessen parallel, wenn sie sich in keinem Punkt schneiden.

Es gibt senkrechte Geraden im Koordinatensystem, die die x-Achse im rechten Winkel schneiden. Sie werden auch vertikale Geraden genannt und verlaufen immer parallel zur y-Achse. Ihre Funktionsgleichung lautet immer x = C , dabei ist C eine beliebige Konstante.

Zwei senkrechte Ebenen im Raum stehen im rechten Winkel zueinander. Um senkrechte Ebenen im Raum zu ermitteln, benötigst du das Skalarprodukt. Wenn das Skalarprodukt ihrer Normalvektoren 0 ergibt, stehen die Ebenen senkrecht zueinander.

Senkrechte Striche kannst du für viele Zeichnungen verwenden. Zum Beispiel brauchst du sie für Häuserzeichnungen: Die Strecken für die Länge und Breite der Fenster sollten senkrecht zueinander stehen, so auch die Strecken für die Tür. Auch das Dach kannst du durch senkrechte Linien darstellen.

Leave A Comment

Alle Artikel aus dem Fach Mathematik