Ableitungsfunktionen und Ableitungen – Mathematik
Erfahre, wie Ableitungen die Steigung und Krümmung von Funktionen beschreiben. Entdecke die Bedeutung von Ableitungen, Ableitungsregeln und wichtigen Ableitungsfunktionen.
Inhaltsverzeichnis zum Thema Ableitungsfunktionen
Teste dein Wissen
Was ist eine Ableitung?
Frage 1 von 5
Wie bildet man die Ableitungsfunktion und wie kann man die Ableitung berechnen?
Frage 2 von 5
Wie sieht die erste Ableitung aus?
Frage 3 von 5
Was ist die erste und zweite Ableitung?
Frage 4 von 5
Wie funktioniert grafisches Ableiten?
Frage 5 von 5
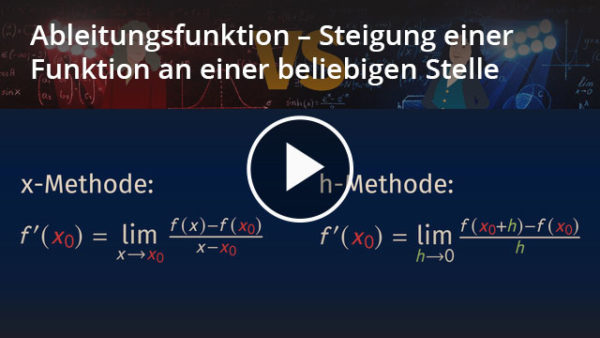
Ableitung und Ableitungsfunktion – Definition
Die Auswertung der ersten Ableitung ![]() gibt die momentane Änderungsrate einer Funktion an der Stelle
gibt die momentane Änderungsrate einer Funktion an der Stelle ![]() an. Mit der Ableitungsfunktion
an. Mit der Ableitungsfunktion ![]() lässt sich die Steigung einer Funktion
lässt sich die Steigung einer Funktion ![]() an jeder beliebigen Stelle berechnen.
an jeder beliebigen Stelle berechnen.
Ableitung Schreibweise: ![]()
ausgesprochen: f Strich von x
Anhand der Ableitung können besondere Punkte des Funktionsgraphen und das Monotonieverhalten der Funktion bestimmt werden. Das Monotonieverhalten gibt an, in welchen Bereichen der Graph steigt oder fällt.
Ableitungsfunktion mit Differenzenquotienten annähern
Die Steigung einer Geraden, die durch zwei Punkte auf einem Graphen verläuft (Sekante), wird durch den Differenzenquotienten angegeben. Der Differenzenquotient beschreibt die mittlere Änderungsrate der Funktion in einem Intervall. Er berechnet sich als:
![]()
Statt ![]() können wir auch
können wir auch ![]() schreiben.
schreiben.
Um die Steigung in einem Punkt ![]() zu berechnen, verkleinern wir den Abstand zwischen den beiden Punkten immer weiter. So nähern wir uns einer Tangente an (eine Gerade, die den Graphen nur an einem Punkt berührt). Mathematisch können wir das durch den Limes (Grenzwert) von
zu berechnen, verkleinern wir den Abstand zwischen den beiden Punkten immer weiter. So nähern wir uns einer Tangente an (eine Gerade, die den Graphen nur an einem Punkt berührt). Mathematisch können wir das durch den Limes (Grenzwert) von ![]() gegen
gegen ![]() beschreiben:
beschreiben:
![]()
Das Ergebnis ist die Steigung der Funktion an der Stelle ![]() :
:
![]()
Dieser Grenzwert des Differenzenquotienten wird als Differenzialquotient bezeichnet und gibt die Steigung einer Tangente an einem bestimmten Punkt ![]() der Funktion an.
der Funktion an.
Bedeutung der Ableitungsfunktion
Mit der Ableitungsfunktion lässt sich die Steigung einer Funktion in jedem Punkt berechnen. Aus der Ableitung können wir ablesen, ob die Funktion an der Stelle ![]() steigt, fällt oder sich bei
steigt, fällt oder sich bei ![]() eine waagrechte Tangente befindet:
eine waagrechte Tangente befindet:
![]() Funktion steigt im Punkt
Funktion steigt im Punkt ![]() .
.
![]() Funktion fällt im Punkt
Funktion fällt im Punkt ![]() .
.
![]() Funktion hat am Punkt
Funktion hat am Punkt ![]() eine waagrechte Tangente.
eine waagrechte Tangente.
Höhere Ableitungen
Neben der ersten Ableitung ![]() (1. Ableitungsfunktion) existieren weitere Ableitungen.
(1. Ableitungsfunktion) existieren weitere Ableitungen.
Wird die erste Ableitung abgeleitet, erhalten wir die zweite Ableitung ![]() . Diese gibt die Änderung der Steigung des Graphen (also die Krümmung der Funktion) in jedem Punkt an. Mit der zweiten Ableitung lassen sich die Wendepunkte der Funktion ermitteln.
. Diese gibt die Änderung der Steigung des Graphen (also die Krümmung der Funktion) in jedem Punkt an. Mit der zweiten Ableitung lassen sich die Wendepunkte der Funktion ermitteln.
In den meisten Fällen ist es nur notwendig, die erste und die zweite Ableitung zu berechnen. Es existieren jedoch noch höhere Ableitungen.
Ableitungen werden in Mathe vor allem bei Kurvendiskussionen verwendet, um Extremstellen und Wendepunkte zu bestimmen.
Ableitung und Integral
Die Gegenrichtung der Ableitung ist das Integral. Leiten wir eine Funktion ab und integrieren sie im Anschluss, landen wir, abgesehen von additiven Konstanten, wieder bei der Ausgangsfunktion. Der Zusammenhang wird als Hauptsatz der Integral- und Differenzialrechnung bezeichnet.
Wichtige Ableitungsfunktionen
Die folgende Tabelle zeigt wichtige Funktionen und deren Ableitungsfunktionen.
| Funktion | Ableitungsfunktion | |
|---|---|---|
| konstante Funktion | ||
| Sinus | ||
| Cosinus | ||
| Tangens | ||
| Logarithmus | ||
| natürlicher Logarithmus | ||
| Exponentialfunktion | ||
| e-Funktion | ||
| Wurzel |
Beim Ableiten einer Funktion müssen verschiedene Regeln beachtet werden. Diese betrachten wir im nächsten Absatz.
Ableitungsfunktion bilden – Regeln
Um die Ableitungsfunktion einer Funktion zu bestimmen, müssen die sogenannten Ableitungsregeln beachtet und angewandt werden.
Potenzregel
Beim Ableiten von ![]() mit einem Exponenten, wird die Zahl aus dem Exponenten als Faktor vor das
mit einem Exponenten, wird die Zahl aus dem Exponenten als Faktor vor das ![]() gezogen und der Exponent um eins verringert.
gezogen und der Exponent um eins verringert.
![]()
Beispiele:
![]()
![]()
Faktorregel
Steht vor dem ![]() ein konstanter Faktor
ein konstanter Faktor ![]() , wird dieser beim Ableiten unverändert stehen gelassen und der Rest der Funktion abgeleitet.
, wird dieser beim Ableiten unverändert stehen gelassen und der Rest der Funktion abgeleitet.
![]()
Beispiel:
![]()
Summen- und Differenzregel
Um die Ableitung einer Summe zu bilden, werden die Summanden getrennt voneinander abgeleitet:
![]()
Für Differenzen gilt das Gleiche:
![]()
Beispiele:
![]()
![]()
Produktregel
Handelt es sich bei der Funktion um ein Produkt aus Funktionen, dann gilt für die Ableitung die Produktregel:
![]()
Das bedeutet, die Ableitung setzt sich zusammen aus der Ableitung des ersten Faktors multipliziert mit dem zweiten Faktor plus erster Faktor multipliziert mit der Ableitung des zweiten Faktors.
Beispiel:
![]()
Zunächst ist es hilfreich, ![]() und
und ![]() und die jeweiligen Ableitungen einzeln aufzuschreiben.
und die jeweiligen Ableitungen einzeln aufzuschreiben.
![]()
![]()
Setzen wir alles einzeln in die oben stehende allgemeine Formel ein, erhalten wir die Ableitung der Funktion:
![]()
Quotientenregel
Soll ein Bruch, bei dem ein ![]() im Zähler und Nenner vorkommt, abgeleitet werden, gilt für die Ableitungsfunktion die Quotientenregel:
im Zähler und Nenner vorkommt, abgeleitet werden, gilt für die Ableitungsfunktion die Quotientenregel:
![]()
Beispiel:
![]()
Zunächst ist es hilfreich, ![]() und
und ![]() und die jeweiligen Ableitungen einzeln aufzuschreiben.
und die jeweiligen Ableitungen einzeln aufzuschreiben.
![]()
![]()
Setzen wir alles einzeln in die oben stehende allgemeine Formel ein, erhalten wir die Ableitung der Funktion:
![]()
Kettenregel
Für verkettete Funktionen wenden wir beim Bilden der Ableitungsfunktion die folgende Formel, die sogenannte Kettenregel, an:
![]()
Beispiel:
![]()
Auch hier ist es sinnvoll, zunächst beide Funktionen und deren Ableitungen einzeln aufzuschreiben.
![]()
![]()
Setzen wir das in die oben stehende Formel ein, erhalten wir die Ableitungsfunktion.
![]()
Ableitungsfunktion berechnen – Beispiele
Berechne die Ableitungsfunktionen der folgenden Funktionen:
![]()
![]()
![]()
![]()
![]()
![]()
Lösungen:
![]()
![]()
![]()
![]()
![]()
![]()
Grafisches Ableiten – Mathe
Die folgende Funktion ![]() (rot-grün-rot) wurde zeichnerisch abgeleitet:
(rot-grün-rot) wurde zeichnerisch abgeleitet:

Bei dem rot-grün-roten Funktionsgraphen handelt es sich um den Graphen der Funktion ![]() . Der blau-lila-blaue Funktionsgraph ist der Graph der Ableitungsfunktion
. Der blau-lila-blaue Funktionsgraph ist der Graph der Ableitungsfunktion ![]() . Es ist gut erkennbar, dass dort, wo die Funktion
. Es ist gut erkennbar, dass dort, wo die Funktion ![]() steigt (rote Abschnitte), die
steigt (rote Abschnitte), die ![]() -Werte des Graphen der Ableitung positiv sind. Im Bereich, wo die Funktion
-Werte des Graphen der Ableitung positiv sind. Im Bereich, wo die Funktion ![]() fällt (grüner Abschnitt), verläuft der Graph der Ableitung unterhalb der
fällt (grüner Abschnitt), verläuft der Graph der Ableitung unterhalb der ![]() -Achse.
-Achse.
Die Ableitungsfunktion hat ihre Nullstellen dort, wo die Funktion ![]() ihre Extremstellen hat. Am Wendepunkt der Funktion
ihre Extremstellen hat. Am Wendepunkt der Funktion ![]() befindet sich der Extrempunkt der Ableitungsfunktion. In diesem Beispiel sehen wir beim grafischen Ableiten sofort, dass der Graph der Ableitungsfunktion eine Parabel ist und die Ableitungsfunktion somit eine quadratische Funktion sein muss.
befindet sich der Extrempunkt der Ableitungsfunktion. In diesem Beispiel sehen wir beim grafischen Ableiten sofort, dass der Graph der Ableitungsfunktion eine Parabel ist und die Ableitungsfunktion somit eine quadratische Funktion sein muss.
Ableiten rückwärts – grafisch
Wir können das grafische Ableiten auch rückwärts durchführen, das bedeutet, dass wir von der Ableitungsfunktion auf Eigenschaften der Ausgangsfunktion schließen können. Dabei orientieren wir uns wieder an den Zusammenhängen der Ausgangsfunktion und ihrer Ableitungsfunktion:
- Dort, wo die Ableitungsfunktion Nullstellen besitzt, hat die Ausgangsfunktion Extremstellen.
- Dort, wo die Ableitungsfunktion einen Extrempunkt besitzt, hat die Ausgangsfunktion einen Wendepunkt.
- Dort, wo die Ableitungsfunktion positive Funktionswerte hat, steigt die Ausgangsfunktion,
- Dort, wo die Ableitungsfunktion negative Funktionswerte hat, fällt die Ausgangsfunktion.
Mithilfe dieser Zusammenhänge können wir die Ausgangsfunktion anhand der Ableitungsfunktion skizzieren.
Hinweis: Ist sonst nichts über die Ausgangsfunktion bekannt, kann deren Graph beliebig in
-Richtung (nach oben oder unten) verschoben sein, da auf Basis der Ableitung nur die
-Werte der charakteristischen Punkte ermittelt werden können.
Ableitungen in Kurvendiskussionen
Ableitungen werden in Kurvendiskussionen genutzt, um Extremstellen und Wendepunkte zu berechnen und das Monotonie- und Krümmungsverhalten zu bestimmen. Dabei werden in der Regel die ersten drei Ableitungen einer Funktion betrachtet.
Monotonieverhalten und Extremstellen bestimmen
Das Monotonieverhalten einer Funktion wird über ihre erste Ableitung bestimmt. In dem Intervall, in dem ![]() ist, steigt die Funktion monoton. Dort, wo
ist, steigt die Funktion monoton. Dort, wo ![]() ist, fällt die Funktion monoton. Um das Monotonieverhalten zu ermitteln, werden zunächst die Nullstellen der ersten Ableitung ermittelt, da hier ein Wechsel im Monotonieverhalten vorliegen kann. Für die Bereiche zwischen den Nullstellen kann dann das Monotonieverhalten beispielsweise durch eine Vorzeichentabelle bestimmt werden. Dabei gilt:
ist, fällt die Funktion monoton. Um das Monotonieverhalten zu ermitteln, werden zunächst die Nullstellen der ersten Ableitung ermittelt, da hier ein Wechsel im Monotonieverhalten vorliegen kann. Für die Bereiche zwischen den Nullstellen kann dann das Monotonieverhalten beispielsweise durch eine Vorzeichentabelle bestimmt werden. Dabei gilt:
- Ein Funktionsgraph ist streng monoton steigend für
 .
. - Ein Funktionsgraph ist monoton steigend für
 .
. - Ein Funktionsgraph ist streng monoton fallend für
 .
. - Ein Funktionsgraph ist monoton fallend für
 .
.
Wir wissen, dass sich dort Extremstellen befinden können, wo die erste Ableitung gleich ![]() ist. Aus diesem Grund ist die notwendige Bedingung:
ist. Aus diesem Grund ist die notwendige Bedingung: ![]() . Um zu prüfen, an welchen Stellen sich Extremstellen befinden, untersuchen wir die Nullstellen der ersten Ableitung, die mögliche Extremstellen sind, genauer.
. Um zu prüfen, an welchen Stellen sich Extremstellen befinden, untersuchen wir die Nullstellen der ersten Ableitung, die mögliche Extremstellen sind, genauer.
Um herauszufinden, ob es sich dabei um Hoch- oder Tiefpunkte handelt, setzen wir diese ![]() -Werte in die zweite Ableitung ein. Die hinreichende Bedingung ist nun:
-Werte in die zweite Ableitung ein. Die hinreichende Bedingung ist nun: ![]() . Zudem gilt:
. Zudem gilt:
- Für
 hat die Funktion bei
hat die Funktion bei 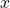 einen Tiefpunkt.
einen Tiefpunkt. - Für
 hat die Funktion bei
hat die Funktion bei 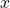 einen Hochpunkt.
einen Hochpunkt. - Für
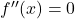 ist keine Aussage möglich. Die Funktion kann bei
ist keine Aussage möglich. Die Funktion kann bei 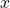 einen Tief-, Hoch- oder Terrassenpunkt haben.
einen Tief-, Hoch- oder Terrassenpunkt haben.
Um die dazugehörigen ![]() -Werte zu berechnen, setzen wir die ermittelten
-Werte zu berechnen, setzen wir die ermittelten ![]() -Werte in die Ausgangsfunktion
-Werte in die Ausgangsfunktion ![]() ein und erhalten somit die
ein und erhalten somit die ![]() -Werte.
-Werte.
Hinweis: Eine alternative Methode, um zu ermitteln, ob es sich bei den Nullstellen der ersten Ableitung um Extrempunkte handelt, ist eine Vorzeichen- oder Monotonietabelle. Dort werden für die Bereiche zwischen den Nullstellen die Vorzeichen der Ableitung ermittelt und daraus wird auf den Verlauf des Funktionsgraphen geschlossen.
Beispiel: ![]()
Erste Ableitung: ![]()
Zweite Ableitung: ![]()
Erste Ableitung null setzen: ![]()
![]()
![]()
Nullstellen der ersten Ableitung in die zweite Ableitung einsetzen:
![]()
![]()
Dazugehörige ![]() -Werte berechnen:
-Werte berechnen:
![]()
![]()
Die Funktion hat einen Tiefpunkt bei ![]() und einen Hochpunkt bei
und einen Hochpunkt bei ![]() .
.
Mithilfe der Extrempunkte können wir nun auf das Monotonieverhalten der Funktion schließen:
- Die Funktion ist im Intervall
![Rendered by QuickLaTeX.com \bigl]- \infty; -1 \bigr] \cup \left[\frac{1}{3}; \infty \right[](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-3094abceaab5cc51a7fa168adf99584b_l3.png) monoton steigend.
monoton steigend. - Die Funktion verläuft im Intervall
![Rendered by QuickLaTeX.com \left[-1; \frac{1}{3} \right]](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-076594c239529f10f60ea1c370c79d5e_l3.png) monoton fallend.
monoton fallend. - Die Funktion ist im Intervall
![Rendered by QuickLaTeX.com \bigl]- \infty; -1 \bigr[ \cup \left]\frac{1}{3}; \infty \right[](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-13b5bfc9f727ceea6aa3ffaa03964512_l3.png) streng monoton steigend.
streng monoton steigend. - Die Funktion verläuft im Intervall
![Rendered by QuickLaTeX.com \left]-1; \frac{1}{3} \right[](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-7f0cbb32b35b1ad4529c710e47bfa67f_l3.png) streng monoton fallend.
streng monoton fallend.
Hinweis: Zeigt die eckige Klammer nach außen, ist die Intervallgrenze nicht im Intervall enthalten. Zeigt sie nach innen, ist die Intervallgrenze Teil des Intervalls.
Krümmungsverhalten und Wendestellen bestimmen
Das Krümmungsverhalten einer Funktion ist an der zweiten Ableitung erkennbar. Dabei gilt:
 ist an der Stelle
ist an der Stelle 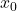 rechtsgekrümmt.
rechtsgekrümmt. ist an der Stelle
ist an der Stelle 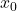 linksgekrümmt.
linksgekrümmt. hat keine Krümmung an der Stelle
hat keine Krümmung an der Stelle 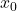 .
.
Rechtsgekrümmt bedeutet, dass die Funktion in einer Rechtskurve verläuft, wenn man sie von links nach rechts betrachtet. Linksgekrümmt bedeutet dementsprechend, dass es sich von links nach rechts betrachtet um eine Rechtskurve handelt.
Kommt in der zweiten Ableitung kein ![]() vor, ändert sich die Krümmung der Funktion nicht und sie ist entweder nur rechtsgekrümmt oder nur linksgekrümmt.
vor, ändert sich die Krümmung der Funktion nicht und sie ist entweder nur rechtsgekrümmt oder nur linksgekrümmt.
Beispiel:
![]()
![]()
![]() linksgekrümmt im ganzen Definitionsbereich
linksgekrümmt im ganzen Definitionsbereich
Kommt in der zweiten Ableitung ein ![]() vor, kann es sein, dass sich die Krümmung der Funktion in ihrem Verlauf ändert. Um zu ermitteln, in welchen Bereichen die Funktion wie gekrümmt ist, überlegen wir, wo die zweite Ableitung kleiner beziehungsweise größer als
vor, kann es sein, dass sich die Krümmung der Funktion in ihrem Verlauf ändert. Um zu ermitteln, in welchen Bereichen die Funktion wie gekrümmt ist, überlegen wir, wo die zweite Ableitung kleiner beziehungsweise größer als ![]() ist. Dafür bestimmen wir zunächst die Nullstellen der zweiten Ableitung, da dies die Punkte sind, an denen ein Wechsel im Krümmungsverhalten auftreten kann.
ist. Dafür bestimmen wir zunächst die Nullstellen der zweiten Ableitung, da dies die Punkte sind, an denen ein Wechsel im Krümmungsverhalten auftreten kann.
Wir können auch direkt die Wendepunkte der Funktion ermitteln und eine Krümmungstabelle aufstellen. Bei einem Wendepunkt ändert sich das Krümmungsverhalten. Somit kann in der Tabelle die Krümmung vor dem ersten Wendepunkt berechnet und anschließend auf das weitere Krümmungsverhalten geschlossen werden.
Dort, wo sich die Krümmung einer Funktion ändert, liegen die Wendestellen. Wir wissen also, dass sich dort Wendestellen befinden, wo die zweite Ableitung gleich ![]() ist. Aus diesem Grund ist die notwendige Bedingung:
ist. Aus diesem Grund ist die notwendige Bedingung:
![]()
Um herauszufinden, ob es sich dabei tatsächlich um Wendepunkte handelt, setzen wir diese ![]() -Werte in die dritte Ableitung ein.
-Werte in die dritte Ableitung ein.
Die hinreichende Bedingung ist nun:
![]()
Hat die dritte Ableitung an der Stelle einen Funktionswert ungleich ![]() , liegt eine Wendestelle vor. Ist der Funktionswert der dritten Ableitung dagegen
, liegt eine Wendestelle vor. Ist der Funktionswert der dritten Ableitung dagegen ![]() , kann keine Aussage getroffen werden, ob an der entsprechenden Stelle eine Änderung im Krümmungsverhalten vorliegt oder nicht.
, kann keine Aussage getroffen werden, ob an der entsprechenden Stelle eine Änderung im Krümmungsverhalten vorliegt oder nicht.
Um die dazugehörigen ![]() -Werte zu berechnen, setzen wir die ermittelten
-Werte zu berechnen, setzen wir die ermittelten ![]() -Werte in die Ausgangsfunktion
-Werte in die Ausgangsfunktion ![]() ein und erhalten somit die
ein und erhalten somit die ![]() -Werte.
-Werte.
Alternativ kann auch eine Krümmungstabelle aufgestellt werden. Daraus lässt sich die Krümmung vor und nach dem Wendepunkt anhand des Vorzeichens der zweiten Ableitung ablesen und somit auf die Lage der Wendepunkte schließen.
Beispiel: ![]()
Erste Ableitung: ![]()
Zweite Ableitung: ![]()
Dritte Ableitung: ![]()
Um die Krümmung zu bestimmen, betrachten wir die zweite Ableitung. Wir überlegen, in welchem Bereich die zweite Ableitung kleiner als ![]() ist. Daraus entsteht die Ungleichung:
ist. Daraus entsteht die Ungleichung:

Es folgt: Für ![]() ist die Funktion rechtsgekrümmt. Nun überlegen wir, in welchem Bereich die zweite Ableitung größer als
ist die Funktion rechtsgekrümmt. Nun überlegen wir, in welchem Bereich die zweite Ableitung größer als ![]() ist:
ist:

Daraus folgt: Für ![]() ist die Funktion linksgekrümmt. Bei
ist die Funktion linksgekrümmt. Bei ![]() liegt dementsprechend ein Wendepunkt. Aber auch diesen können wir rechnerisch ermitteln:
liegt dementsprechend ein Wendepunkt. Aber auch diesen können wir rechnerisch ermitteln:
zweite Ableitung null setzen: ![]()
![]()
Nullstelle der zweiten Ableitung in die dritte Ableitung einsetzen: ![]()
Dazugehörigen ![]() -Wert berechnen:
-Wert berechnen:
![]()
Die Funktion hat einen RL-Wendepunkt bei ![]() . Vor dem Wendepunkt ist die Funktion rechtsgekrümmt. Nach dem Wendepunkt ist sie linksgekrümmt. Aus diesem Grund wird der Wendepunkt als RL-Wendepunkt bezeichnet.
. Vor dem Wendepunkt ist die Funktion rechtsgekrümmt. Nach dem Wendepunkt ist sie linksgekrümmt. Aus diesem Grund wird der Wendepunkt als RL-Wendepunkt bezeichnet.
Alternative Krümmungstabelle
Zunächst werden die Nullstellen der zweiten Ableitung der Funktion berechnet. Für die Funktion ![]() hat die zweite Ableitung eine Nullstelle bei
hat die zweite Ableitung eine Nullstelle bei ![]() .
.
Nun können wir die Krümmung vor dieser Nullstelle berechnen. Dafür setzen wir einen Wert kleiner als ![]() in die zweite Ableitung ein. Ist der Funktionswert größer als
in die zweite Ableitung ein. Ist der Funktionswert größer als ![]() , handelt es sich um eine Linkskrümmung, bei einem negativen Funktionswert um eine Rechtskrümmung:
, handelt es sich um eine Linkskrümmung, bei einem negativen Funktionswert um eine Rechtskrümmung:
![]()
Daraus folgt, dass die Funktion vor der Nullstelle rechtsgekrümmt ist. Für die Krümmungstabelle setzen wir auch einen Wert größer als ![]() in die zweite Ableitung ein und prüfen das Vorzeichen:
in die zweite Ableitung ein und prüfen das Vorzeichen:
| Krümmung | rechtsgekrümmt | Wechsel im Krümmungsverhalten, daraus folgt Wendepunkt | linksgekrümmt |
Häufig gestellte Fragen zu Ableitungsfunktionen