Was ist parallel? – Erklärungen und Aufgaben zu parallelen Linien

Parallele Linien haben überall denselben Abstand zueinander und schneiden sich nie. Erfahre, wie man sie zeichnet, wo sie im Alltag vorkommen und welche Rolle sie im Mathematikunterricht spielen.

Inhaltsverzeichnis zum Thema Was ist parallel?

Was ist parallel? – Überblick

  • Parallele Linien werden als Teilgebiet der Geometrie im Mathematikunterricht behandelt.

  • Linien sind parallel, wenn sie überall den gleichen Abstand voneinander haben.

  • Parallele Linien schneiden sich in keinem Punkt.

  • Im Alltag gibt es viele parallele Linien, zum Beispiel bei Bahngleisen oder bei den Sprossen einer Leiter.

Parallele Linien: Lernvideo

Quelle sofatutor.com

Was sind parallele Linien? – Definition

Zwei Linien sind parallel, wenn sie überall voneinander den gleichen Abstand haben. Parallele Linien schneiden sich also in keinem Punkt.

Das gilt auch für parallele Geraden. Geraden sind gerade Linien, die du in beide Richtungen beliebig verlängern kannst. Schau dir die Geraden im folgenden Bild an. Sind sie parallel oder schneiden sie sich in einem Punkt?

Parallele Geraden

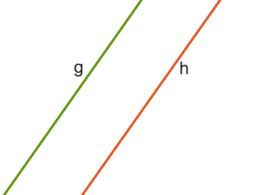
Die Geraden sind parallel, da sie überall den gleichen Abstand voneinander haben. Auch wenn du die Geraden in beide Richtungen verlängerst, werden sie sich nie schneiden.

Parallele und senkrechte Linien

Du weißt nun, dass parallele Linien keinen Schnittpunkt haben, deshalb schneiden sie sich auch in keinem Winkel.
Nicht parallele Linien haben dagegen immer mindestens einen Schnittpunkt. Besondere, nicht parallele Linien sind senkrechte Linien. Senkrechte Linien schneiden sich in einem 90^\circ-Winkel. Der eingeschlossene Winkel wird auch rechter Winkel genannt.

Senkrechte Geraden

In der folgenden Tabelle bekommst du noch einmal eine Übersicht über parallele und senkrechte Linien.

Parallele Linien Senkrechte Linien
überall der gleiche Abstand unterschiedliche Abstände
kein Schnittpunkt Schnittpunkt

Parallele Linien zeichnen/konstruieren

Um parallele Linien zu zeichnen, kannst du dein Geodreieck verwenden. Dort sind zur längsten Kante parallele Linien eingezeichnet. Zeichne nun eine Linie und lege eine der eingezeichneten parallelen Linien genau auf deine Linie. Nun kannst du eine Linie entlang der längsten Strecke des Geodreiecks zeichnen und schon hast du zwei zueinander parallele Linien.

Zeichnen einer parallelen Strecke

Es gibt noch eine weitere Möglichkeit, eine parallele Linie zu zeichnen. Dazu zeichnest du von der ersten Linie aus mithilfe deines Geodreiecks zwei senkrechte Strecken, die gleich lang sind. Die Endpunkte dieser beiden senkrechten Linien verbindest du nun miteinander und hast somit eine parallele Linie gezeichnet.

Parallele Linien im Alltag

In der Natur und im Alltag kannst du viele parallele Linien erkennen. Zum Beispiel sind die Bahngleise für Züge immer parallel zueinander. Wären sie das nicht, würden die Züge entgleisen.

Parallele Linien bei Bahngleisen

Parallele Linien gibt es oftmals in der Architektur. Kannst du im folgenden Bild die parallelen Linien erkennen?

Parallele Linien im Alltag

Die beiden Hauptstraßen sind parallel zueinander. Und auch bei einigen der Häuser gibt es parallele Linien. 

Im Musikunterricht sind dir sicher auch schon einmal parallele Linien aufgefallen – das Notensystem besteht aus fünf zueinander parallelen Linien, auf denen die Töne durch Zeichen dargestellt werden.

Notenlinien

In der Kunst werden parallele Linien eingesetzt, um in der Parallelperspektive zu zeichnen. Alle Linien in die Tiefe verlaufen dabei parallel. So wird der Eindruck von Dreidimensionalität erzeugt. Im Gegensatz dazu gibt es auch die Fluchtpunktperspektive, bei der sich alle Linien in die Tiefe in einem Punkt schneiden.

Parallele Linien bei geometrischen Formen

Viele geometrische Formen besitzen parallele Linien.

Die gegenüberliegenden Seiten eines Rechtecks sind parallel zueinander.

Rechteck

Auch das Quadrat als besonderes Rechteck besitzt somit parallele Linien.

Quadrat

Eine weitere Form mit parallelen Linien ist das Parallelogramm. Welche Linien sind parallel zueinander?

Parallelogramm

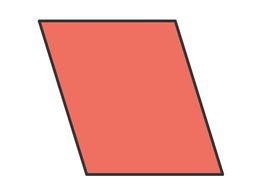
Beim Parallelogramm sind ebenfalls die gegenüberliegenden Seiten zueinander parallel. Somit gehören auch alle Rechtecke und Quadrate zu den Parallelogrammen.

Ein Trapez hat hingegen nur ein paar paralleler Seiten.

Trapez

Parallelität im Mathematikunterricht der weiterführenden Schule

Im Folgenden kannst du Erklärungen und Aufgaben zur Parallelität nachlesen, die in der weiterführenden Schule, also ab der fünften Klasse thematisiert werden.

Parallele Linien und parallele Ebenen

Nicht nur Linien in der Ebene, sondern auch Ebenen im Raum können parallel sein. Zwei Ebenen sind parallel, wenn sie keine gemeinsamen Punkte und keine gemeinsame Schnittgerade haben.

Parallele Ebenenschar

Parallele Linien und Kongruenz

Kongruenzabbildungen sind Abbildungen, bei denen die Form und Größe der Figur nicht verändert werden. Dabei bleiben Längen gleich lang und Winkel gleich groß. 

Die Verschiebung ist eine Kongruenzabbildung. Für die Verschiebung gilt die Parallelentreue. Das bedeutet, dass Gerade und Bildgerade parallel zueinander sind.

Parallele Linien – Aufgaben für Klasse 5 und Klasse 6

In der fünften und sechsten Klasse lernst du, wie du parallele Linien konstruieren kannst.

Außerdem kannst du mithilfe deines Geodreiecks überprüfen, ob zwei Linien tatsächlich parallel zueinander sind.

Parallele Linien – Aufgaben für Klasse 7

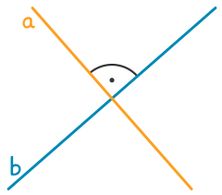
Wenn zwei verschiedene parallele Linien eine dritte Linie schneiden, entstehen acht Winkel, die besondere Winkelbeziehungen haben. Um die Winkelmaße zu berechnen, musst du den Satz über Stufenwinkel, Wechselwinkel, Nebenwinkel und den Satz über Scheitelwinkel kennen.

Probiere, diese Aufgabe zu lösen. Der Winkel \alpha hat 140 ^\circ. Wie groß ist dann der Winkel \beta?

Winkelarten

Hier musst du den Satz über Neben- und Stufenwinkel anwenden. Da g und h parallele Linien sind, ist die Winkelsumme der Nebenwinkel \alpha und \beta = 180 ^\circ. Deshalb kannst du \beta so berechnen: \beta = 180^\circ - 140^\circ = 40 ^\circ.

Parallele Linien – Aufgaben für Klasse 8

In einem Koordinatensystem kannst du berechnen, ob zwei Linien bzw. Geraden parallel sind.
Du hast beispielsweise die Geraden y = 3x + 6 und y = 3x + 5. Sind die beiden Geraden parallel?
Ja, sie sind parallel, denn die Steigung m = 3 ist bei beiden Geraden gleich. Nur der y-Achsenabschnitt unterscheidet sich.

Alternativ kannst du auch die Funktionsgleichungen gleichsetzen:

3x + 6 = 3x + 5

Nun ziehst du 3x ab und es bleibt folgende Gleichung übrig:

6 = 5

Das ist eine falsche Aussage, was bedeutet, dass das Gleichungssystem keine Lösung und somit auch keinen Schnittpunkt hat. Die beiden Geraden sind also parallel zueinander, weil sie sich in keinem Punkt schneiden.

Parallele Linien – Aufgaben für Klasse 9

Bei Dreiecken kannst du Mittellinien einzeichnen. Das sind Linien, die entstehen, wenn du die Mittelpunkte der Dreiecksseiten miteinander verbindest. Diese Linien sind parallel zu den Seiten des Dreiecks.

Mittellinien im Dreieck

Aufgabe: parallele Linien und rechtwinklige Dreiecke
Auch bei rechtwinkligen Dreiecken kannst du die Mittellinien einzeichnen. Probiere es einmal selbst aus. Zeichne ein rechtwinkliges Dreieck mit den Seitenlängen a = 3~\text{cm}, b = 4~\text{cm} und c = 5~\text{cm}. Zeichne nun die Mittellinien des Dreiecks. Wie lange sind die Mittellinien?
Tipp: Jede Mittellinie ist halb so lang wie die zu ihr parallele Dreiecksseite.

Parallele Linien – Aufgaben für Klasse 10

Zwei Geradenlinien im dreidimensionalen Raum sind parallel, wenn die Richtungsvektoren Vielfache voneinander sind und der Aufpunkt der einen Gerade sich nicht auf der anderen Gerade befindet.

Sind diese beiden Geraden parallel?
g: \vec{x} = \begin{pmatrix} 4 \\ 0 \\ 4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix}
h: \vec{x} = \begin{pmatrix} 8 \\ 4 \\ 8 \end{pmatrix} + \mu \cdot \begin{pmatrix} -2 \\ -4 \\ -2 \end{pmatrix}
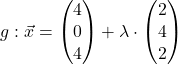
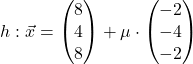
Zuerst überprüfst du Bedingung 1, also ob die Richtungsvektoren Vielfache voneinander sind.
Dazu kannst du überlegen, ob es eine Zahl gibt, mit der du den Richtungsvektor der ersten Gerade multiplizieren kannst und damit den Richtungsvektor der zweiten Gerade erreichst.
\begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix} = r \cdot \begin{pmatrix} -2 \\ -4 \\ -2 \end{pmatrix}
Nun kannst du Zeile für Zeile jeweils den r-Wert berechnen:
2 = r \cdot (-2) \rightarrow r = -1
4 = r \cdot (-4) \rightarrow r = -1
2 = r \cdot (-2) \rightarrow r = -1
r nimmt für alle Zeilen den gleichen Wert an. Das bedeutet also, dass die Richtungsvektoren Vielfache voneinander sind.

Nun musst du noch überprüfen, ob die Geraden parallel oder identisch sind. Dazu musst du den Aufpunkt der einen Gerade mit der Geradengleichung der anderen Gerade gleichsetzen.
\begin{pmatrix} 8 \\ 4 \\ 8 \end{pmatrix} = \begin{pmatrix} 4 \\ 0 \\ 4 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix}
Jetzt berechnest du Zeile für Zeile den Wert von \lambda.
8 = 4 + \lambda \cdot 2 \rightarrow \lambda = 2
4 = 0 + \lambda \cdot 4 \rightarrow \lambda = 1
8 = 4 + \lambda \cdot 2 \rightarrow \lambda = 2
\lambda nimmt nicht in allen Zeilen den gleichen Wert an. Das bedeutet, dass die Geraden nicht identisch sind und damit echte parallele Geraden sind.

Weiterführende Informationen: parallele Linien und Kreuzprodukt
Zwei Geraden im Raum sind außerdem zueinander parallel, wenn das Kreuzprodukt ihrer Richtungsvektoren gleich 0 ist.

Häufig gestellte Fragen zum Thema Was ist Parallel?

Parallele Linien haben überall voneinander den gleichen Abstand und schneiden sich nie.

Parallele Linien haben die Eigenschaften, dass sie überall voneinander den gleichen Abstand und keinen Schnittpunkt haben.

Der Abstand zwischen zwei parallelen Linien ist überall gleich groß.

Parallele Linien schneiden sich in keinem Punkt, auch nicht im Unendlichen.

Parallele Linien kannst du mithilfe der zur längsten Seite parallelen Hilfslinien auf dem Geodreieck zeichnen. Lege eine dieser Hilfslinien auf deine Linie. Zeichne dann entlang der längsten Kante des Geodreiecks eine weitere Linie. Diese ist parallel zur ersten Linie.

Während parallele Linien keinen Schnittpunkt haben, schneiden sich senkrechte Linien im 90^\circ-Winkel.

Wenn zwei verschiedene parallele Linien eine dritte Linie schneiden, entstehen acht Winkel, die besondere Winkelbeziehungen haben. Um die Winkelmaße zu berechnen, musst du die Winkelsätze kennen.

Zwei Geraden sind parallel, wenn sie überall den gleichen Abstand voneinander haben und sich in keinem Punkt schneiden. Im dreidimensionalen Raum sind zwei Geraden echt parallel, wenn sie durch eine Verschiebung identisch werden.

Windschiefe Geraden gibt es nur im dreidimensionalen Raum. Sie haben ebenfalls keinen Schnittpunkt, sind aber nicht parallel zueinander.

Zwei Geraden im Koordinatensystem sind parallel zueinander, wenn sie die gleiche Steigung haben und sich nur der y-Achsenabschnitt unterscheidet.

Parallele Linien gibt es bei Bahngleisen oder bei Sprossen von Leitern. Auch in der Architektur gibt es viele parallele Linien, zum Beispiel bei Häusern.

In der Kunst werden parallele Linien eingesetzt, um in der Parallelperspektive zu zeichnen.

Bei Parallelogrammen sind die gegenüberliegenden Seiten parallel zueinander.

Zwei Geraden im dreidimensionalen Raum sind parallel, wenn die Richtungsvektoren Vielfache voneinander sind und der Aufpunkt der einen Gerade sich nicht auf der anderen Gerade befindet.

Zwei Geraden im Raum sind außerdem zueinander parallel, wenn das Kreuzprodukt ihrer Richtungsvektoren gleich 0 ist.

Eine Ebene ist eine flache, zweidimensionale Oberfläche, die sich ins Unendliche erstreckt. Eine Gerade ist hingegen eine gerade, unendlich lange und unendlich dünne, in beide Richtungen unbegrenzte Linie.

Quellen zum Thema Was ist parallel?

martin-missfeldt.de, Was ist die Parallelperspektive?,

https://www.martin-missfeldt.de/perspektive-zeichnen-tutorial/parallelperspektive.php

Leave A Comment

Alle Artikel aus dem Fach Mathematik