Transformation Mathe – Definition, Grundlagen und Beispiele
Entdecke die Vielfalt der Transformationen in Analysis und Geometrie. Strecke, stauche und verschiebe Funktionen, oder erkunde Spiegelungen und Drehungen von geometrischen Figuren. Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Transformation Mathe
Transformationen von Funktionen – Grundlagen und Formeln
In der Analysis kannst du Funktionen mithilfe von Parametern transformieren. Bei der Transformation von Funktionen wird unterschieden in:
- Verschiebung in
 -Richtung,
-Richtung, - Verschiebung in
 -Richtung und
-Richtung und - Streckung und Stauchung.
Verschiebung einer Funktion in ![]() -Richtung
-Richtung
Betrachte beispielhaft die Normalparabel mit der Funktionsgleichung ![]() .
.
Möchtest du diese in Richtung der ![]() -Achse verschieben, kannst du dies tun, indem du
-Achse verschieben, kannst du dies tun, indem du
- zu
 einen entsprechenden Wert addierst, um die Funktion nach links zu verschieben,
einen entsprechenden Wert addierst, um die Funktion nach links zu verschieben, - oder von
 einen entsprechenden Wert subtrahierst, um die Funktion nach rechts zu verschieben.
einen entsprechenden Wert subtrahierst, um die Funktion nach rechts zu verschieben.
Dies kannst du nicht nur mit der Normalparabel machen, sondern mit allen Funktionen. Allgemein formuliert bedeutet das:
Eine Funktion ![]() wird durch eine Verschiebung des Funktionsgraphen um
wird durch eine Verschiebung des Funktionsgraphen um ![]() Einheiten in
Einheiten in ![]() -Richtung zu der Funktion
-Richtung zu der Funktion ![]() transformiert. Die Konstante
transformiert. Die Konstante ![]() nimmt entsprechend der Verschiebungsrichtung positive oder negative Werte an. Ist
nimmt entsprechend der Verschiebungsrichtung positive oder negative Werte an. Ist ![]() , liegt eine Verschiebung um
, liegt eine Verschiebung um ![]() Einheiten nach rechts vor. Ist
Einheiten nach rechts vor. Ist ![]() , handelt es sich um eine Verschiebung um
, handelt es sich um eine Verschiebung um ![]() Einheiten nach links.
Einheiten nach links.
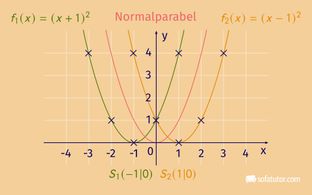
Zurück zum Beispiel der Normalparabel: Die Funktionsgleichung der Normalparabel, die um eine Einheit nach rechts auf der ![]() -Achse verschoben ist, lautet also
-Achse verschoben ist, lautet also ![]() .
.
Entsprechend lautet die Funktionsgleichung der Normalparabel, die um eine Einheit nach links verschoben ist, ![]() .
.
Verschiebung einer Funktion in ![]() -Richtung
-Richtung
Du kannst eine Funktion auch in Richtung der ![]() -Achse verschieben. Dafür
-Achse verschieben. Dafür
- addierst du einen Wert zur Funktionsgleichung, um die Funktion nach oben zu verschieben,
- oder subtrahierst den Wert, wenn die Funktion nach unten verschoben werden soll.
Eine Funktion ![]() wird durch eine Verschiebung des Funktionsgraphen um
wird durch eine Verschiebung des Funktionsgraphen um ![]() Einheiten in
Einheiten in ![]() -Richtung zu der Funktion
-Richtung zu der Funktion ![]() transformiert. Ist
transformiert. Ist ![]() , wird der Funktionsgraph nach oben verschoben, für
, wird der Funktionsgraph nach oben verschoben, für ![]() nach unten.
nach unten.
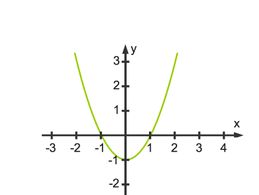
Zum Beispiel ist die Normalparabel auf dem folgenden Bild um eine Einheit nach unten verschoben und ihre Funktionsgleichung lautet ![]() .
.
Streckung und Stauchung von Funktionen
Bei der Streckung bzw. Stauchung einer Funktion wird zwischen zwei Fällen unterschieden:
Die Streckung/Stauchung in ![]() -Richtung:
-Richtung: ![]()
Die Streckung/Stauchung in ![]() -Richtung:
-Richtung: ![]()
Bei der Streckung bzw. Stauchung in ![]() -Richtung wird der gesamte Funktionsterm mit der Konstante
-Richtung wird der gesamte Funktionsterm mit der Konstante ![]() multipliziert, während bei der Streckung bzw. Stauchung in
multipliziert, während bei der Streckung bzw. Stauchung in ![]() -Richtung nur der
-Richtung nur der ![]() -Wert mit der Konstanten
-Wert mit der Konstanten ![]() multipliziert wird.
multipliziert wird.
Dabei gilt für ![]() :
:
- Ist
 größer als
größer als 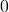 und kleiner als
und kleiner als 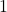 , wird der Graph in
, wird der Graph in  -Richtung gestreckt.
-Richtung gestreckt. - Ist
 größer als
größer als 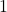 , wird der Graph in
, wird der Graph in  -Richtung gestaucht.
-Richtung gestaucht. - Ist
 wird der Graph an der
wird der Graph an der  -Achse gespiegelt.
-Achse gespiegelt.
Und für ![]() :
:
- Ist
 größer als
größer als 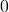 und kleiner als
und kleiner als 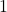 , wird der Graph in
, wird der Graph in  -Richtung gestaucht.
-Richtung gestaucht. - Ist
 größer als
größer als 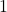 , wird der Graph in
, wird der Graph in  -Richtung gestreckt.
-Richtung gestreckt. - Ist
 wird der Graph an der
wird der Graph an der  -Achse gespiegelt.
-Achse gespiegelt.
Beispiel für Streckung und Stauchung in ![]() -Richtung:
-Richtung:

Bei der Funktion ![]() ist der Vorfaktor
ist der Vorfaktor ![]() und somit ist dieser kleiner als
und somit ist dieser kleiner als ![]() und größer als
und größer als ![]() . Die Normalparabel wird hier also um den Faktor
. Die Normalparabel wird hier also um den Faktor ![]() in
in ![]() -Richtung gestaucht.
-Richtung gestaucht.

Die Funktion ![]() besitzt den Vorfaktor
besitzt den Vorfaktor ![]() . Dieser ist größer als
. Dieser ist größer als ![]() , das bedeutet, dass die Normalparabel mit dem Faktor
, das bedeutet, dass die Normalparabel mit dem Faktor ![]() in
in ![]() -Richtung gestreckt wird.
-Richtung gestreckt wird.
Funktionsgleichungen einer Parabel kannst du immer in die sogenannte Scheitelpunktform umformen. Anhand dieser Schreibweise kannst du die verschiedenen Parameter und somit die Transformationen direkt ablesen.
Beispiel für Streckung und Stauchung in ![]() -Richtung:
-Richtung:
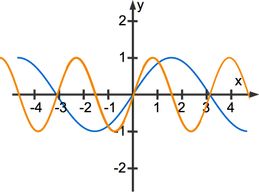
Der blaue Funktionsgraph bildet die Sinusfunktion ![]() ab. Der orangefarbene Funktionsgraph ist eine transformierte Sinusfunktion. Diese wurde durch eine Stauchung in
ab. Der orangefarbene Funktionsgraph ist eine transformierte Sinusfunktion. Diese wurde durch eine Stauchung in ![]() Richtung erzeugt:
Richtung erzeugt: ![]() .
.
Weitere Transformationen in der Mathematik
Nicht nur in der Analysis gibt es Transformationen, sondern auch in der Geometrie und der Stochastik sind Transformationen zu finden. Wie diese in den unterschiedlichen Teilgebieten definiert sind, lernst du im Folgenden.
Geometrische Transformation – Mathe
In der Geometrie fasst der Begriff Transformation die folgenden Operationen zusammen:
- Spiegelungen (Achsen- und Punktspiegelungen)
- Drehungen
- Verschiebungen
- Streckungen
Diese kannst du an jeder beliebigen geometrischen Figur und ebenso in der Raumgeometrie anwenden.
So ist beispielsweise die Spiegelung dieses Dreiecks an einer Spiegelachse eine Transformation.
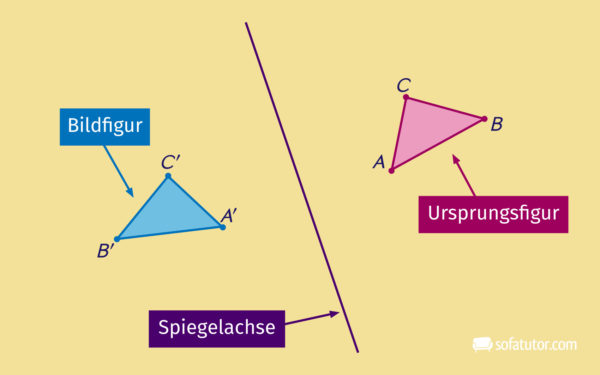
Aber auch die Streckung eines Dreiecks kann als Transformation verstanden werden.
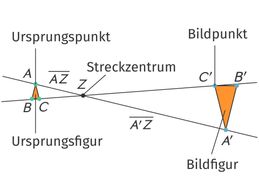
Transformation mit Matrizen – Mathe
Im Abitur können dir Transformationen in Mathe noch in einem weiteren Inhaltsfeld begegnen: den Übergangsmatrizen.
Sie beschreiben Zustandsveränderungen. Die einzelnen Einträge der Matrix geben die prozentualen Zu- beziehungsweise Abwanderungen an.
Stell dir vor, ![]() ,
, ![]() und
und ![]() wären die Eisdielen deiner Stadt.
wären die Eisdielen deiner Stadt.
Dann würden jede Woche beispielsweise
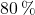 der Kunden von Eisdiele
der Kunden von Eisdiele 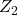 bei der Eisdiele
bei der Eisdiele 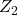 bleiben,
bleiben,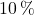 der Kunden von Eisdiele
der Kunden von Eisdiele  zu Eisdiele
zu Eisdiele 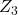 wechseln,
wechseln,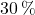 der Kunden von Eisdiele
der Kunden von Eisdiele  zu Eisdiele
zu Eisdiele 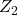 wechseln
wechseln- usw.
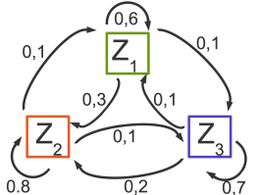
Diese Zustandsveränderung lässt sich auch mit der folgenden Matrix darstellen.

Transformation Mathe – Zusammenfassung und Aufgaben
In der folgenden Tabelle sind verschiedene Transformationen zusammengefasst, die dir in der Schule begegnen können.
| Teilgebiet in Mathe | Art der Transformation | Beispiel |
|---|---|---|
| Analysis | Streckung/Stauchung in |
|
| Streckung/Stauchung in |
||
| Verschiebung in |
||
| Verschiebung in |
||
| Geometrie | Spiegelungen Drehungen Verschiebungen Streckungen |
Achsenspiegelung eines Dreiecks |
| Matrizen | Übergangsmatrizen |  |
Teste dein Wissen über die Transformationen in Mathe doch gleich an ein paar Übungen:
Welche Transformation kannst du an dieser Funktion erkennen?
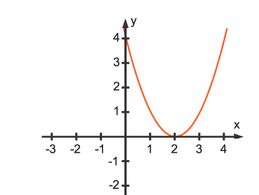
Es handelt sich um eine Normalparabel, die um zwei Einheiten entlang der ![]() -Achse nach rechts verschoben wurde. Die Funktionsgleichung lautet also
-Achse nach rechts verschoben wurde. Die Funktionsgleichung lautet also ![]() .
.
Und wie ist es bei folgender Funktion?
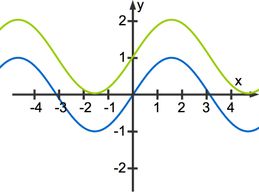
Die blaue Funktion ist die normale Sinusfunktion ![]() . Der grüne Funktionsgraph ist eine um eine Einheit in
. Der grüne Funktionsgraph ist eine um eine Einheit in ![]() -Richtung verschobene Sinusfunktion. Ihre Funktionsgleichung lautet
-Richtung verschobene Sinusfunktion. Ihre Funktionsgleichung lautet ![]() .
.
Häufig gestellte Fragen zum Thema Transformation Mathe

