Ganzrationale Funktionen
Lerne, was ganzrationale Funktionen sind und wie sie definiert sind. Entdecke verschiedene Arten wie konstante, lineare, quadratische und kubische Funktionen. Lerne über Eigenschaften wie Symmetrie, Grenzwerte, Nullstellen, Extrema und Wendepunkte. Interessiert? Dies und vieles mehr im folgenden Text.
Inhaltsverzeichnis zum Thema Ganzrationale Funktionen
Ganzrationale Funktionen – Definition
Als ganzrationale Funktionen oder Polynomfunktionen werden Funktionen, deren Funktionsgleichung folgende Form hat, bezeichnet:
![]()
Dabei gilt:
![]()
Der Grad der Funktion wird durch den höchsten Exponenten (![]() ), der bei der Variablen
), der bei der Variablen ![]() auftaucht, festgelegt. Ist
auftaucht, festgelegt. Ist ![]() , handelt es sich um eine ganzrationale Funktion dritten Grads.
, handelt es sich um eine ganzrationale Funktion dritten Grads.
Die Werte ![]() werden als Koeffizienten des Polynoms bezeichnet.
werden als Koeffizienten des Polynoms bezeichnet.
Die Funktionsgraphen ganzrationaler Funktionen haben je nach Grad ![]() und den Werten der einzelnen Koeffizienten
und den Werten der einzelnen Koeffizienten ![]() mit
mit ![]() verschiedene Verläufe.
verschiedene Verläufe.
Wir definieren die ganzrationalen Funktionen stets in Abgrenzung zu gebrochen rationalen Funktionen oder anderen Funktionstypen.
Die Bezeichnung der ganzrationalen Funktionen leitet sich daraus ab, dass es sich bei den Exponenten ausschließlich um natürliche Zahlen handelt.
Werden Variablen mit Vorfaktoren und Exponenten addiert, subtrahiert oder multipliziert, sprechen wir von einem Polynom. Da bei ganzrationalen Funktionen Variablen mit Vorfaktoren und Exponenten addiert werden, sprechen wir auch von Polynomfunktionen.
Ganzrationale Funktion – Beispiel
![]()
Ganzrationale Funktionen – Begriffe
Um die verschiedenen Begriffe zu klären, betrachten wir die folgende Beispielfunktion:
![]()
Als ganzrationale Funktion oder Polynomfunktion 4. Grads wird der gesamte Ausdruck bezeichnet. Es handelt sich um eine Funktion 4. Grads, da der höchste Exponent, der bei der Variablen ![]() auftritt,
auftritt, ![]() ist.
ist.
Als Koeffizienten werden die Faktoren vor den Potenzen bezeichnet, in diesem Fall also ![]() und
und ![]() . Als Leitkoeffizient wird der Faktor vor der höchsten Potenz bezeichnet, in diesem Fall ist der Leitkoeffizient
. Als Leitkoeffizient wird der Faktor vor der höchsten Potenz bezeichnet, in diesem Fall ist der Leitkoeffizient ![]() .
.
Besteht eine Funktion nur aus einem Leitkoeffizienten und einer Potenz, wird sie auch als Potenzfunktion bezeichnet.
Besondere ganzrationale Funktionen
Innerhalb der ganzrationalen Funktionen werden verschiedene Arten von Funktionen herausgestellt, diese unterscheiden sich hauptsächlich durch ihren Grad.
Konstante Funktion (ganzrationale Funktion 0. Grads)
Konstante Funktionen sind unabhängig von ![]() , da
, da ![]() gilt. Sie werden auch als ganzrationale Funktionen 0. Grads bezeichnet. Die allgemeine Funktionsgleichung lautet demnach:
gilt. Sie werden auch als ganzrationale Funktionen 0. Grads bezeichnet. Die allgemeine Funktionsgleichung lautet demnach:
![]()
Konstante Funktionen verlaufen parallel zur ![]() -Achse und schneiden die
-Achse und schneiden die ![]() -Achse an der Stelle
-Achse an der Stelle ![]() .
.
Beispiel
![]()

Lineare Funktion (ganzrationale Funktion 1. Grads)
Bei linearen Funktionen handelt es sich um ganzrationale Funktionen 1. Grads. Die Variable ![]() kommt nur mit der Potenz
kommt nur mit der Potenz ![]() vor, es gilt:
vor, es gilt: ![]() . Die allgemeine Funktionsgleichung lautet:
. Die allgemeine Funktionsgleichung lautet:
![]()
Hierbei entspricht ![]() und
und ![]() .
.
Lineare Funktionen haben die Steigung ![]() und schneiden die
und schneiden die ![]() -Achse an der Stelle
-Achse an der Stelle ![]() (
(![]() -Achsenabschnitt).
-Achsenabschnitt).
Beispiel
![]()

Quadratische Funktion (ganzrationale Funktion 2. Grads)
Bei quadratischen Funktionen handelt es sich um ganzrationale Funktionen 2. Grads. Ihr Funktionsgraph verläuft als Parabel. Die allgemeine Funktionsgleichung lautet:
![]()
Hierbei entspricht ![]() ,
, ![]() und
und ![]() .
.
Beispiel
![]()
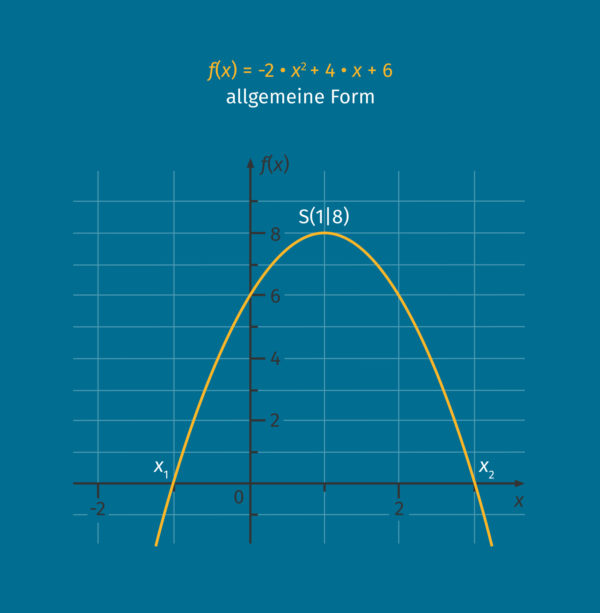
Kubische Funktion (ganzrationale Funktion 3. Grads)
Ganzrationale Funktionen 3. Grads werden als kubische Funktionen bezeichnet. Ihre allgemeine Funktionsgleichung lautet:
![]()
Beispiel
![]()

Ganzrationale Funktion (ganzrationale Funktion 4. Grads)
Für ganzrationale Funktionen 4. Grads gibt es keinen speziellen Namen. Ihre allgemeine Funktionsgleichung lautet:
![]()
Beispiel
![]()

Ganzrationale Funktion – Eigenschaften und Funktionsuntersuchung
Die Eigenschaften ganzrationaler Funktionen unterscheiden sich je nachdem, welchen Grad die Funktion hat. Dieser muss bei der Untersuchung einer ganzrationalen Funktion oder bei Kurvendiskussionen immer beachtet werden.
Ganzrationale Funktion – Symmetrie
Achsensymmetrie
Für achsensymmetrische Funktionen gilt:
![]()
Ganzrationale Funktionen sind achsensymmetrisch, wenn sie nur gerade Exponenten besitzen.
Beispiel: ![]()
![]()
Punktsymmetrie
Für punktsymmetrische Funktionen gilt:
![]()
Ganzrationale Funktionen sind punktsymmetrisch, wenn sie nur ungerade Exponenten besitzen.
Beispiel:
![]()
![]()
Ganzrationale Funktion – Grenzwerte
Der Grad und das Vorzeichen des Leitkoeffizienten ![]() bestimmen die Grenzwerte, also das Verhalten im Unendlichen, einer ganzrationalen Funktion.
bestimmen die Grenzwerte, also das Verhalten im Unendlichen, einer ganzrationalen Funktion.
Gerader Grad
Ganzrationale Funktionen mit einem geraden Grad ähneln, was ihren Verlauf im Unendlichen angeht, einer Parabel. Wir unterscheiden dabei zwei Möglichkeiten:
| Vorzeichen Leitkoeffizient | Grenzwert |
|---|---|
| Leitkoeffizient |
|
| Leitkoeffizient |
Ungerader Grad
Ganzrationale Funktionen mit einem ungeraden Grad ähneln im Unendlichen dem Verlauf einer Geraden. Auch hier beeinflusst das Vorzeichen des Leitkoeffizienten das Verhalten im Unendlichen.
| Vorzeichen Leitkoeffizient | Grenzwert |
|---|---|
| Leitkoeffizient |
|
| Leitkoeffizient |
Ganzrationale Funktion – Nullstellen berechnen
Die Nullstellen einer Funktion berechnen wir immer, indem wir diese gleich null setzt:
![]()
Je nach Grad der Funktion wird diese auf verschiedene Weisen aufgelöst:
- Lineare Funktionen: Term einfach auflösen
- Quadratische Funktionen: Mitternachtsformel oder pq-Formel anwenden
- Höherer Grad: Ausklammern oder Polynomdivision (wenn bereits eine Nullstelle bekannt ist)
Auf die genaue Berechnung der Nullstellen wird im Text Nullstellen berechnen eingegangen.
Allgemein gilt: Die Anzahl der Nullstellen einer ganzrationalen Funktion ist kleiner oder gleich dem Grad der Funktion. Eine ganzrationale Funktion 4. Grads kann also maximal vier Nullstellen besitzen. Außerdem hat eine ganzrationale Funktion mit ungeradem Grad stets mindestens eine Nullstelle, ganzrationale Funktionen mit geradem Grad können auch keine Nullstellen haben.
Ganzrationale Funktion – Extrema
Um die Extremstellen (Minimum, Maximum und Sattelpunkte) einer ganzrationale Funktion zu bestimmen, gehen wir folgendermaßen vor:
- Erste Ableitung bilden
- Nullstellen der ersten Ableitung bestimmen
- Zugehörige
 -Werte durch Einsetzen in die Ausgangsfunktion ermitteln
-Werte durch Einsetzen in die Ausgangsfunktion ermitteln - Art der Extrempunkte durch Einsetzen in die zweite Ableitung oder das Vorzeichenwechselkriterium bestimmen
Eine ganzrationale Funktion vom Grad ![]() kann maximal
kann maximal ![]() Extrempunkte besitzen.
Extrempunkte besitzen.
Eine genaue Erklärung zum Bilden der Ableitung findest du im Text zu den Ableitungsfunktionen.
Ganzrationale Funktion – Wendepunkte
Um die Wendepunkte einer ganzrationale Funktion zu bestimmen, gehen wir folgendermaßen vor:
- Zweite Ableitung bilden
- Nullstellen der zweiten Ableitung bestimmen
- Zugehörige
 -Werte durch Einsetzen in die Ausgangsfunktion ermitteln
-Werte durch Einsetzen in die Ausgangsfunktion ermitteln - Art der Wendepunkte durch Einsetzen in die dritte Ableitung oder das Vorzeichenwechselkriterium bestimmen
Es gilt: Jede ganzrationale Funktion mit einem ungeraden Grad größer gleich drei hat mindestens einen Wendepunkt.
Eine ganzrationale Funktion vom Grad ![]() kann maximal
kann maximal ![]() Wendepunkte besitzen.
Wendepunkte besitzen.
Rekonstruktion von ganzrationalen Funktionen
Rekonstruktion bedeutet, dass aus gegebenen Informationen über die Funktion (z. B. Nullstellen, Extremstellen, Symmetrie …) die Funktionsgleichung aufgestellt wird. Die wichtigste Information ist dabei der Grad der Funktion. Mithilfe des Grads kann die allgemeine Funktionsgleichung aufgestellt werden. Erst dann kann die Rekonstruktion richtig beginnen.
Mit der Symmetrie kann eine Aussage über die Exponenten der Funktion getroffen werden:
- Achsensymmetrisch
 nur gerade Exponenten
nur gerade Exponenten - Punktsymmetrisch
 nur ungerade Exponenten
nur ungerade Exponenten
Es können auch Punkte, die auf dem Graphen liegen, gegeben sein:
- Ist der Punkt
 gegeben, gilt:
gegeben, gilt:
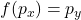
- Geht der Graph durch den Ursprung, dann gilt:

Sind Informationen über Extrempunkte, die Steigung oder eine Tangente gegeben, muss immer mit der ersten Ableitung gearbeitet werden, da mit dieser die Steigung ganzrationaler Funktionen berechnet wird:
- Liegt an der Stelle
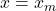 eine Extremstelle (Maximum oder Minimum), gilt:
eine Extremstelle (Maximum oder Minimum), gilt:
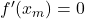
- Besitzt der Graph an der Stelle
 die Steigung
die Steigung 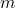 , gilt:
, gilt:

- Hat die Funktion an der Stelle
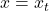 eine Tangente mit der Funktionsgleichung
eine Tangente mit der Funktionsgleichung 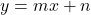 , gilt:
, gilt:
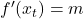
Sind Informationen über Wendestellen gegeben, muss mit der zweiten Ableitung gearbeitet werden:
- Liegt an der Stelle
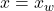 eine Wendestelle, gilt:
eine Wendestelle, gilt:
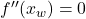
- Hat die Funktion an der Stelle
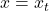 eine Wendetangente mit der Funktionsgleichung
eine Wendetangente mit der Funktionsgleichung 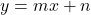 , gilt:
, gilt:
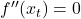 und
und 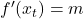
Rekonstruktion – Beispielrechnung
Gegebene Informationen
Eine Funktion 3. Grads schneidet die ![]() -Achse bei
-Achse bei ![]() und die
und die ![]() -Achse bei
-Achse bei ![]() . Sie hat einen Hochpunkt bei
. Sie hat einen Hochpunkt bei ![]() .
.
Vorgehensweise
Mithilfe dieser Informationen können wir schrittweise die Funktionsgleichung aufstellen.
Allgemeine Funktionsgleichung einer Funktion 3. Grads aufstellen:
![]() schneidet die
schneidet die ![]() -Achse bei
-Achse bei ![]() :
:
- Es gilt:

- Daraus folgt:
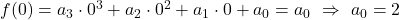
![]() schneidet die
schneidet die ![]() -Achse bei
-Achse bei ![]() :
:
- Es gilt:

- Daraus folgt:
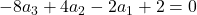
![]() hat einen Hochpunkt bei
hat einen Hochpunkt bei ![]() :
:
- Es gilt:

- Daraus folgt:

- Und es gilt:

- Daraus folgt:

Aus den damit erhaltenen Gleichungen kann ein Gleichungssystem mit drei Gleichungen aufgestellt werden. So können die Werte für ![]() ,
, ![]() und
und ![]() berechnet werden:
berechnet werden:
![]()
![]()
![]()
Funktionsgleichung aufstellen
Setzen wir diese Werte in die allgemeine Funktionsgleichung ein, erhalten wir die gesuchte ganzrationale Funktion. Diese lautet:
![]()
Rekonstruktion – Aufgabe: ganzrationale Funktion aufstellen
Es soll die Funktionsgleichung einer ganzrationalen Funktion mit den folgenden Eigenschaften bestimmt werden:
Eine Funktion 3. Grads schneidet die ![]() -Achse bei
-Achse bei ![]() . Sie hat einen Hochpunkt bei
. Sie hat einen Hochpunkt bei ![]() . Zudem ist
. Zudem ist ![]() .
.
Lösung
Allgemeine Funktionsgleichung einer Funktion 3. Grads mit ![]() aufstellen:
aufstellen:
Graph schneidet die ![]() -Achse bei
-Achse bei ![]() :
:
- Es gilt:

- Daraus folgt:

Hochpunkt bei ![]()
- Es gilt:

- Daraus folgt:

- Und es gilt:

- Daraus folgt:
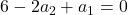
Aus den damit erhaltenen Gleichungen kann ein Gleichungssystem mit zwei Gleichungen aufgestellt werden. So können die Werte für ![]() und
und ![]() berechnet werden:
berechnet werden:
![]()
![]()
Setzen wir diese Werte in die allgemeine Formel ein, erhalten wir die gesuchte ganzrationale Funktion. Diese lautet:
![]()
Ganzrationale Funktionen – Gegenbeispiele
Beispiele für ganzrationale Funktionen hast du bereits kennengelernt. Nicht zu den ganzrationalen Funktionen gehören:
- die Exponentialfunktionen (
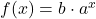 ),
), - die Wurzelfunktionen (
![Rendered by QuickLaTeX.com f(x) = \sqrt[n]{x}](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-8f38130a126c6b7d17c85f432f68cf91_l3.png) ),
), - die trigonometrischen Funktionen (
 ,
, 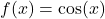 und
und  ) und
) und - die gebrochen rationalen Funktionen (
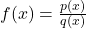 ).
).
Häufig gestellte Fragen zum Thema Ganzrationale Funktionen

