Geradengleichung – Formen, Erklärung und Beispiele

In der Mathematik sind Geradengleichungen bei linearen Funktionen und in der Vektorrechnung zu finden. Sie beschreiben allgemein eine Menge von Punkten in Form einer Geraden.

Bei einer linearen Funktion wird ein linearer Zusammenhang zwischen zwei Größen und durch eine Gerade veranschaulicht. In den meisten Fällen wird hierzu die folgende Formel für eine Geradengleichung in allgemeiner Form verwendet:

Dabei steht der Parameter in der Geradengleichung für die Steigung der Geraden, der Parameter gibt den -Achsenabschnitt der Geraden an. Eine solche Darstellung der Form wird auch explizite Form genannt.
Da es sich um eine lineare Funktion handelt, schreibt man auch .

Als implizite Geradengleichung werden Gleichungen bezeichnet, bei denen die abhängige Variable nicht allein steht, zum Beispiel: .
Durch Umstellen der Gleichung können wir auch diese in eine explizite Form bringen:

Wir wollen nun einige typische Fragestellungen zum Thema betrachten. Unter anderem, wie wir eine Geradengleichung zu einer Geraden ermitteln, die bestimmte Eigenschaften erfüllt. Dazu erklären wir, wie wir die verschiedenen Elemente der Geradengleichung berechnen können.

Wir bestimmen die Geradengleichung einer linearen Funktion aus den zwei Punkten und .
Die Steigung ist der Quotient aus der Differenz der – und -Werte:

Wir setzen und den Punkt in die allgemeine Form ein und berechnen :

Wir erhalten für die Gerade durch und die Gleichung:

Für die Geradengleichung einer Geraden , die senkrecht zu einer anderen Geraden verlaufen soll, muss für die Steigungen und von und gelten:

Eine Tangente ist eine Gerade, die den Graphen einer anderen Funktion in einem Punkt berührt (tangiert). Wir können die Geradengleichung dieser Tangente mit einem Punkt und der Steigung des Funktionsgraphen in diesem Punkt bestimmen.
Für die Tangente an die Funktion in einem Berührpunkt gilt:

• Die Steigung der Tangente entspricht der Ableitung der Funktion bei :
  
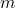• Der -Achsenabschnitt kann durch Einsetzen von und 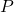ermittelt werden:
  

Um die passende Gerade zu einer Geradengleichung in ein Koordinatensystem einzuzeichnen, gibt es verschiedene Möglichkeiten.
Durch Einsetzen von zwei beliebigen -Werten in die Geradengleichung können die Koordinaten von zwei Punkten, die auf der Geraden liegen, bestimmt werden. Diese tragen wir dann in ein Koordinatensystem ein und zeichnen die Gerade durch die Punkte.

Wir lesen den Schnittpunkt mit der -Achse aus der Geradengleichung ab:

Diesen Punkt markieren wir im Koordinatensystem und zeichnen von dort ein Steigungsdreieck mit den Längen aus .

Hier siehst du den Graphen der Geraden mit der Geradengleichung . Aus der Gleichung können wir den -Achsenabschnitt und die Steigung ablesen. Damit können wir die Gerade folgendermaßen einzeichnen.
Sie geht durch den Punkt auf der -Achse.
Für das Steigungsdreieck gehen wir nach rechts und dann nach oben.
Wir zeichnen die Gerade durch diese beiden Punkte.

Um anhand der Geradengleichung zu überprüfen, ob ein Punkt auf einer Geraden liegt, wird die sogenannte Punktprobe verwendet. Dazu werden die Koordinaten des Punkts in die Geradengleichung eingesetzt. Erhalten wir dabei eine wahre Aussage, dann folgern wir, dass die Gerade durch den Punkt verläuft. Eine falsche Aussage bedeutet entsprechend, dass der überprüfte Punkt nicht auf der Geraden liegt.

Mithilfe der Geradengleichung lässt sich der Schnittpunkt von zwei Geraden berechnen. Dazu werden die Funktionsgleichungen der beiden Geraden gleichgesetzt. Da zwei Geraden nicht immer einen gemeinsamen Schnittpunkt haben müssen, können drei Fälle auftreten:

Hinweis: Parallele Geraden erkennst du auch daran, dass sie die gleiche Steigung haben.

Im Raum werden Geradengleichungen in der Parameterform mit Vektoren angegeben. Die allgemeine Form lautet:

Dabei ist der Stützvektor und der Richtungsvektor der Geraden.

Im Raum können wir eine Geradengleichung durch zwei Punkte und folgendermaßen angeben:

• Der Richtungsvektor ist ein beliebiges Vielfaches des Verbindungsvektors . Wir rechnen:
  
• Wir wählen
• Als Stützvektor 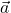wählen wir den Ortsvektor

Wir erhalten durch Einsetzen von und in für die Gerade durch und im Raum die Gleichung:

Für die Geradengleichung einer Geraden , die im Raum senkrecht zu einer anderen Geraden verlaufen soll, muss für die Richtungsvektoren und von und gelten:

Um anhand der Geradengleichung zu überprüfen, ob ein Punkt auf einer Geraden liegt, wird die sogenannte Punktprobe verwendet. Dazu wird der Ortsvektor des Punkts für in die Geradengleichung eingesetzt. Finden wir einen Wert für den Parameter , für den in allen Komponenten eine wahre Aussage entsteht, dann folgern wir, dass die Gerade durch den Punkt verläuft. Tritt in mindestens einer Komponente eine falsche Aussage auf, bedeutet dies entsprechend, dass der überprüfte Punkt nicht auf der Geraden liegt.