Lineare Funktionen – Begriffe, Erklärung und Beispiele
Lineare Funktionen sind Geradengleichungen, bei denen ![]() nur in erster Potenz vorkommt. Entdecke, wie man die Funktionsgleichung aufstellt, die Steigung berechnet und den
nur in erster Potenz vorkommt. Entdecke, wie man die Funktionsgleichung aufstellt, die Steigung berechnet und den ![]() -Achsenabschnitt findet. Dies und vieles mehr findest du im folgenden Text!
-Achsenabschnitt findet. Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Lineare Funktionen
Lineare Funktion – Definition
Lineare Funktionen (Geradengleichungen) sind in Mathe Funktionen, in denen ![]() nur in der ersten Potenz vorkommt. Die Funktionsgraphen linearer Funktionen sind Geraden im Koordinatensystem. Sie können steigen, fallen oder waagerecht verlaufen.
nur in der ersten Potenz vorkommt. Die Funktionsgraphen linearer Funktionen sind Geraden im Koordinatensystem. Sie können steigen, fallen oder waagerecht verlaufen.
Lineare Funktion – Funktionsgleichung
Die Funktionsgleichung einer linearen Funktion hat die Form:
![]()
Dabei ist:
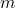 : die Steigung der Geraden
: die Steigung der Geraden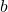 : der
: der  -Achsenabschnitt
-Achsenabschnitt
Normalerweise werden Funktionen immer ![]() genannt. Dabei steht
genannt. Dabei steht ![]() für den Funktionswert, also
für den Funktionswert, also ![]() . Wir können aus diesem Grund auch schreiben:
. Wir können aus diesem Grund auch schreiben:
![]()
Jeder Funktionsterm, der in dieser Form dargestellt werden kann, beschreibt eine lineare Funktion.
Beispiele:
- Lineare Funktion:


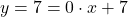
- Keine lineare Funktion:

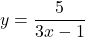
Lineare Funktionen – Steigung
Die Steigung ![]() gibt an, wie stark eine Gerade im Koordinatensystem steigt oder fällt. Wir unterscheiden dabei drei Möglichkeiten:
gibt an, wie stark eine Gerade im Koordinatensystem steigt oder fällt. Wir unterscheiden dabei drei Möglichkeiten:
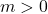 : Die Gerade steigt.
: Die Gerade steigt. : Die Gerade fällt.
: Die Gerade fällt.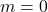 : Die Gerade verläuft waagerecht.
: Die Gerade verläuft waagerecht.
Die Beispielfunktion ![]() hat eine positive Steigung (
hat eine positive Steigung (![]() ) und steigt somit.
) und steigt somit.
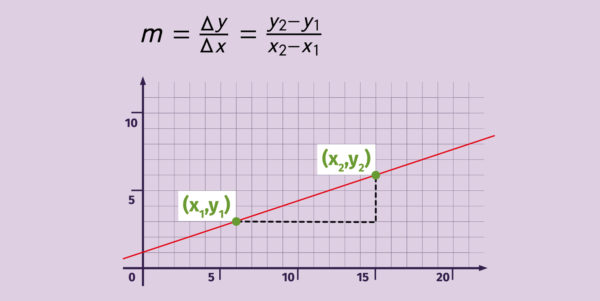
Die Steigung einer linearen Funktion lässt sich mithilfe eines Steigungsdreiecks direkt am Funktionsgraphen bestimmen. Dazu werden zunächst zwei beliebige Punkte auf der Geraden gewählt. Nun kann das Steigungsdreieck eingezeichnet werden. Dafür ziehen wir eine Linie vom linken Punkt waagerecht nach rechts bis zur ![]() -Koordinate des rechten Punkts. Dann zeichnen wir eine zweite Linie von dort senkrecht nach oben oder unten zum zweiten Punkt auf der Geraden. Die beiden Linien ergeben zusammen mit dem Funktionsgraphen das Steigungsdreieck.
-Koordinate des rechten Punkts. Dann zeichnen wir eine zweite Linie von dort senkrecht nach oben oder unten zum zweiten Punkt auf der Geraden. Die beiden Linien ergeben zusammen mit dem Funktionsgraphen das Steigungsdreieck.
Quelle sofatutor.com
Die Steigung ![]() ergibt sich nun als Quotient aus der Länge der senkrechten Linie und der Länge der waagerechten Linie. Für die Berechnung der Steigung einer linearen Funktion ergibt sich somit die Formel:
ergibt sich nun als Quotient aus der Länge der senkrechten Linie und der Länge der waagerechten Linie. Für die Berechnung der Steigung einer linearen Funktion ergibt sich somit die Formel:
![]()
Dabei sind ![]() und
und ![]() die Koordinaten des ersten Punkts und
die Koordinaten des ersten Punkts und ![]() und
und ![]() die Koordinaten des zweiten Punkts.
die Koordinaten des zweiten Punkts.
Beispiel:
Im oben dargestellten linearen Funktionsgraphen sind die Punkte ![]() und
und ![]() markiert. Um die Steigung der Funktion zu berechnen, setzen wir die Koordinaten in die Formel zur Berechnung von
markiert. Um die Steigung der Funktion zu berechnen, setzen wir die Koordinaten in die Formel zur Berechnung von ![]() ein und erhalten:
ein und erhalten:
![]()
Die Steigung der oben dargestellten Funktion beträgt also ![]() .
.
Lineare Funktionen – ![]() -Achsenabschnitt
-Achsenabschnitt ![]() berechnen
berechnen
Der ![]() -Achsenabschnitt ist der Wert, an dem eine Gerade die
-Achsenabschnitt ist der Wert, an dem eine Gerade die ![]() -Achse schneidet. Jede lineare Funktion besitzt genau einen Schnittpunkt mit der
-Achse schneidet. Jede lineare Funktion besitzt genau einen Schnittpunkt mit der ![]() -Achse. Da es sich um einen Punkt handelt, hat dieser Schnittpunkt auch einen
-Achse. Da es sich um einen Punkt handelt, hat dieser Schnittpunkt auch einen ![]() -Wert. Dieser ist immer
-Wert. Dieser ist immer ![]() . Bei
. Bei ![]() handelt es sich um den
handelt es sich um den ![]() -Wert des Schnittpunkts.
-Wert des Schnittpunkts.
Der ![]() -Achsenabschnitt linearer Funktionen kann in vielen Fällen am Graphen abgelesen werden. Er lässt sich aber auch rechnerisch bestimmen, wenn die Steigung gegeben ist. Dafür setzen wir die Steigung
-Achsenabschnitt linearer Funktionen kann in vielen Fällen am Graphen abgelesen werden. Er lässt sich aber auch rechnerisch bestimmen, wenn die Steigung gegeben ist. Dafür setzen wir die Steigung ![]() sowie die
sowie die ![]() – und
– und ![]() -Koordinaten eines Punkts auf der Geraden in die Geradengleichung ein. Indem wir die Gleichung nach
-Koordinaten eines Punkts auf der Geraden in die Geradengleichung ein. Indem wir die Gleichung nach ![]() umstellen, erhalten wir den
umstellen, erhalten wir den ![]() -Achsenabschnitt.
-Achsenabschnitt.
![]()
![]()
Beispiel:
Setzen wir ![]() und die berechnete Steigung der oben dargestellten Funktion ein, erhalten wir also
und die berechnete Steigung der oben dargestellten Funktion ein, erhalten wir also ![]() -Achsenabschnitt:
-Achsenabschnitt:
![]()
Den berechneten Wert für ![]() können wir mit dem Funktionsgraphen vergleichen und sehen, dass dieser die
können wir mit dem Funktionsgraphen vergleichen und sehen, dass dieser die ![]() -Achse bei
-Achse bei ![]() schneidet.
schneidet.
Lineare Funktionen – Nullstellen
Die Stelle, an der ein Graph die ![]() -Achse schneidet, wird Nullstelle genannt. Eine Gerade besitzt maximal eine Nullstelle. Um diese Nullstelle
-Achse schneidet, wird Nullstelle genannt. Eine Gerade besitzt maximal eine Nullstelle. Um diese Nullstelle ![]() zu berechnen, setzen wir in die Funktionsgleichung für
zu berechnen, setzen wir in die Funktionsgleichung für ![]() die
die ![]() ein, da an der Nullstelle
ein, da an der Nullstelle ![]() immer den Wert
immer den Wert ![]() hat.
hat.
![]()
Stellen wir diese Gleichung nach ![]() um, erhalten wir:
um, erhalten wir:

![]()
Die Nullstelle liegt also immer bei ![]() .
.
Da Nullstellen Punkte sind, können diese in der Form ![]() angegeben werden.
angegeben werden.
Hinweis: Für waagrechte Geraden mit ![]() ist der Term nicht definiert. Diese haben keinen Schnittpunkt mit der
ist der Term nicht definiert. Diese haben keinen Schnittpunkt mit der ![]() -Achse.
-Achse.
Beispiel:
Betrachten wir noch einmal die oben dargestellte Funktion. Setzen wir ![]() und
und ![]() in die Formel für die Nullstelle ein, erhalten wir für
in die Formel für die Nullstelle ein, erhalten wir für ![]() :
:
![]()
Der Graph der Funktion schneidet die ![]() -Achse an der Stelle
-Achse an der Stelle ![]() .
.
Lineare Funktionen – Gleichung aufstellen
Ist der Graph einer Funktion gegeben, dann lässt sich mithilfe der Punkt-Steigungs-Form die Funktionsgleichung des Graphen der linearen Funktion aus zwei Punkten bestimmen. Dafür gehst du folgendermaßen vor:
- Wähle zwei Punkte, die auf der Gerade liegen.
- Berechne die Steigung des Graphen mithilfe der Formel:

- Die berechnete Steigung und die
 – und
– und  -Werte eines Punkts setzt du nun in die Funktionsgleichung
-Werte eines Punkts setzt du nun in die Funktionsgleichung 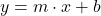 ein und stellst diese nach
ein und stellst diese nach 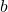 um.
um. - Im letzten Schritt setzt du die berechneten Werte für
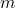 und
und 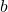 in die allgemeine Funktionsgleichung
in die allgemeine Funktionsgleichung 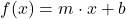 ein.
ein.
Beispiel:
Betrachten wir den Graphen einer linearen Funktion.
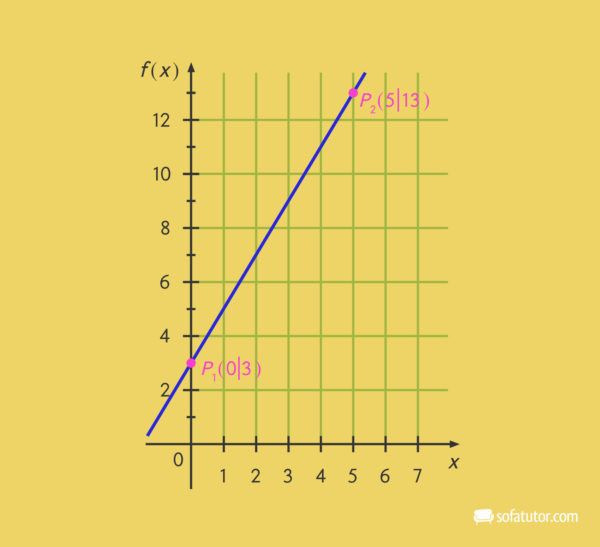
Auf der Geraden sind bereits die zwei Punkte ![]() und
und ![]() markiert. Diese setzen wir in die Steigungsformel ein, um
markiert. Diese setzen wir in die Steigungsformel ein, um ![]() zu ermitteln.
zu ermitteln.
![]()
Nun können wir die berechnete Steigung und die Koordinaten eines Punkts in die nach ![]() umgestellte Funktionsgleichung einsetzen und erhalten für den
umgestellte Funktionsgleichung einsetzen und erhalten für den ![]() -Achsenabschnitt:
-Achsenabschnitt:
![]()
Die Funktionsgleichung der dargestellten Funktion lautet:
![]()
Lineare Funktion – Graphen zeichnen
Um eine lineare Funktion im Koordinatensystem zu zeichnen, gehst du in folgenden Schritten vor:
- Aus der Funktionsgleichung den
 -Achsenabschnitt
-Achsenabschnitt 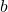 ablesen
ablesen - Schnittpunkt mit der
 -Achse einzeichnen
-Achse einzeichnen - Ausgehend von diesem Schnittpunkt ein Steigungsdreieck (
 ) einzeichnen und einen weiteren Punkt markieren
) einzeichnen und einen weiteren Punkt markieren - Gerade durch beide Punkte ziehen
Beispiel:
Schauen wir uns das Zeichnen einer linearen Funktion am Beispiel von ![]() an.
an.
Zunächst können wir den ![]() -Achsenabschnitt aus der Funktionsgleichung ablesen. Da
-Achsenabschnitt aus der Funktionsgleichung ablesen. Da ![]() gilt, wissen wir, dass der Graph der Funktion die
gilt, wissen wir, dass der Graph der Funktion die ![]() -Achse bei
-Achse bei ![]() schneidet. Diesen Punkt markieren wir im Koordinatensystem.
schneidet. Diesen Punkt markieren wir im Koordinatensystem.
Mithilfe der Steigung können wir nun ein Steigungsdreieck einzeichnen. Da ![]() , gehen wir dafür
, gehen wir dafür ![]() Kästchen vom Schnittpunkt mit der
Kästchen vom Schnittpunkt mit der ![]() -Achse nach rechts und ein Kästchen nach oben. Wir landen somit beim Punkt
-Achse nach rechts und ein Kästchen nach oben. Wir landen somit beim Punkt ![]() . Wir können nun eine Gerade durch diese beiden Punkte zeichnen und erhalten den Graphen der Funktion.
. Wir können nun eine Gerade durch diese beiden Punkte zeichnen und erhalten den Graphen der Funktion.

Eine weitere Möglichkeit, lineare Funktionen zu zeichnen, ist es, eine Wertetabelle anzufertigen. Dabei werden verschiedene Werte für ![]() gewählt und die dazugehörigen
gewählt und die dazugehörigen ![]() -Werte berechnet. Die errechneten Punkte der linearen Funktion werden im Anschluss in das Koordinatensystem eingezeichnet und zum Graphen der Funktion verbunden.
-Werte berechnet. Die errechneten Punkte der linearen Funktion werden im Anschluss in das Koordinatensystem eingezeichnet und zum Graphen der Funktion verbunden.
Lage von Geraden
Zwei Geraden können entweder parallel zueinander verlaufen oder sie haben einen eindeutigen Schnittpunkt. Zwei parallele Geraden haben immer die gleiche Steigung. Bei parallelen Geraden unterscheiden wir zudem in echt parallel und identisch. Echt parallele Geraden haben keine gemeinsamen Punkte, während identische Geraden komplett gleich sind, sie besitzen die gleiche Funktionsgleichung.
Anhand der Funktionsgleichung kannst du sofort ablesen, ob zwei Geraden sich schneiden, echt parallel oder identisch sind.
- Steigung von zwei Geraden ist verschieden: Geraden besitzen einen eindeutigen Schnittpunkt.
- Steigung ist gleich, aber
 -Achsenabschnitt ist unterschiedlich: Geraden sind echt parallel.
-Achsenabschnitt ist unterschiedlich: Geraden sind echt parallel. - Steigung und
 -Achsenabschnitt sind gleich: Geraden sind identisch.
-Achsenabschnitt sind gleich: Geraden sind identisch.
Waagerechte und senkrechte Geraden
Lineare Funktionen mit der Steigung ![]() verlaufen immer waagerecht. Ihre Funktionsgleichung lautet
verlaufen immer waagerecht. Ihre Funktionsgleichung lautet ![]() . Außer der Funktion
. Außer der Funktion ![]() (unendlich viele Nullstellen) besitzen waagerechte lineare Funktionen keine Nullstellen.
(unendlich viele Nullstellen) besitzen waagerechte lineare Funktionen keine Nullstellen.
Senkrechte Geraden sind keine linearen Funktionen, da sie sich nicht in der Form ![]() darstellen lassen. Die Steigung dieser Funktionen ist unendlich und ihre Gleichung lautet
darstellen lassen. Die Steigung dieser Funktionen ist unendlich und ihre Gleichung lautet ![]() , wobei
, wobei ![]() eine beliebige Zahl ist.
eine beliebige Zahl ist.
Lineare Funktion – Schnittpunkte berechnen
In manchen Fällen kannst du den Schnittpunkt zweier Geraden einfach ablesen. Genauer ist es jedoch, den Schnittpunkt rechnerisch zu bestimmen. Dafür gehen wir folgendermaßen vor:
- Beide Funktionsterme gleichsetzen
- Gleichung nach
 auflösen
auflösen  in die erste Funktionsgleichung einsetzen und
in die erste Funktionsgleichung einsetzen und  berechnen
berechnen- Probe:
 in die zweite Funktionsgleichung einsetzen und Ergebnis mit dem ersten vergleichen
in die zweite Funktionsgleichung einsetzen und Ergebnis mit dem ersten vergleichen
Beispiel:
Betrachten wir die Funktionen:
![]()
![]()
Zunächst setzen wir beide Funktionen gleich.
![]()
Nun stellen wir die Gleichung so um, dass ![]() auf einer Seite allein steht.
auf einer Seite allein steht.

Wir erhalten für ![]() den Wert
den Wert ![]() . Den
. Den ![]() -Wert des Schnittpunkts haben wir somit erhalten. Setzen wir die
-Wert des Schnittpunkts haben wir somit erhalten. Setzen wir die ![]() in eine der beiden Funktionsgleichungen ein, erhalten wir den dazugehörigen
in eine der beiden Funktionsgleichungen ein, erhalten wir den dazugehörigen ![]() -Wert:
-Wert:
![]()
![]()
Um zu überprüfen, ob der Schnittpunkt ![]() richtig ist, können wir nun den
richtig ist, können wir nun den ![]() -Wert in die zweite Gleichung einsetzen. Für
-Wert in die zweite Gleichung einsetzen. Für ![]() müssen wir den gleichen Wert wie für
müssen wir den gleichen Wert wie für ![]() erhalten:
erhalten:
![]()
![]()
Die beiden Geraden ![]() und
und ![]() schneiden sich im Punkt
schneiden sich im Punkt ![]() .
.
Lineare Funktionen – Aufgaben
Das gerade erlernte Wissen kannst du nun bei den folgenden Aufgaben anwenden.
Lineare Funktion einzeichnen
Gegeben ist die Funktionsgleichung:
![]()
Aufgabe ist es, diese lineare Funktion in einem Koordinatensystem darzustellen. Wie gehst du vor?
Lösung:
Schritt 1: ![]() -Achsenabschnitt aus der Funktionsgleichung ablesen:
-Achsenabschnitt aus der Funktionsgleichung ablesen:
![]()
Schritt 2: ![]() -Achsenabschnitt im Koordinatensystem abtragen
-Achsenabschnitt im Koordinatensystem abtragen
Schritt 3: Mithilfe der Steigung ![]() ein Steigungsdreieck einzeichnen. Dafür beliebig viele Schritte (zum Beispiel
ein Steigungsdreieck einzeichnen. Dafür beliebig viele Schritte (zum Beispiel ![]() ) nach rechts gehen, die Anzahl der Schritte mit
) nach rechts gehen, die Anzahl der Schritte mit ![]() multiplizieren (
multiplizieren (![]() ) und diese Anzahl an Schritten nach oben/unten gehen. Da es sich um einen negativen Wert handelt, gehen wir
) und diese Anzahl an Schritten nach oben/unten gehen. Da es sich um einen negativen Wert handelt, gehen wir ![]() Schritte nach unten.
Schritte nach unten.
Schritt 4: Zweiten Punkt markieren:
![]()
Schritt 5: Gerade durch beide Punkte zeichnen

Lineare Funktion – Merkmale erkennen und Funktionsgleichung aufstellen
Der folgende Funktionsgraph ist gegeben:

Bestimme zunächst anhand des Graphen die wichtigsten Eigenschaften dieser linearen Funktion. Stelle im Anschluss die Funktionsgleichung auf.
Lösung:
Die aus dem Graphen erkennbaren Merkmale der Funktion sind:
- Die Funktion steigt,
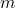 muss also positiv sein.
muss also positiv sein. - Die Funktion schneidet die
 -Achse bei
-Achse bei  .
. - Die Nullstelle der Funktion liegt im negativen
 -Bereich.
-Bereich.
Um die Funktionsgleichung dieser Gerade zu ermitteln, suchen wir uns zunächst zwei Punkte auf der Geraden. In diesem Beispiel sind bereits die Punkte ![]() und
und ![]() markiert. Wir ermitteln die Steigung
markiert. Wir ermitteln die Steigung ![]() , indem wir beide Punkte in die Steigungsformel einsetzen:
, indem wir beide Punkte in die Steigungsformel einsetzen:
![]()
Den ![]() -Achsenabschnitt
-Achsenabschnitt ![]() erhalten wir, indem wir die berechnete Steigung und die Koordinaten eines Punkts in die nach
erhalten wir, indem wir die berechnete Steigung und die Koordinaten eines Punkts in die nach ![]() umgestellte Funktionsgleichung einsetzen:
umgestellte Funktionsgleichung einsetzen:
![]()
Die Funktionsgleichung der dargestellten Funktion lautet:
![]()
Häufig gestellte Fragen zum Thema Lineare Funktionen

