Urnenmodelle in der Mathematik

Urnenmodelle in der Mathematik sind Modelle für Zufallsexperimente, die verschiedene Arten des Ziehens von Kugeln aus einer Urne beschreiben. Erfahre, wie Ziehen mit und ohne Zurücklegen sowie mit und ohne Berücksichtigung der Reihenfolge funktioniert.

Inhaltsverzeichnis zum Thema Urnenmodelle

Urnenmodelle – Definition und Eigenschaften
Urnenmodelle als Zufallsexperimente
Ziehen mit Zurücklegen mit Berücksichtigung der Reihenfolge
Ziehen mit Zurücklegen ohne Berücksichtigung der Reihenfolge
Ziehen ohne Zurücklegen mit Berücksichtigung der Reihenfolge
Ziehen ohne Zurücklegen ohne Berücksichtigung der Reihenfolge
Urnenmodelle – Formeln mit Herleitung
Formeln zu Urnenmodellen im Überblick
Häufig gestellte Fragen zum Thema Urnenmodelle

Das Quiz zum Thema: Urnenmodell

Was sind Urnenmodelle in der Mathematik?

Frage 1 von 5

Was beschreibt ein Laplace-Experiment?

Frage 2 von 5

Welche Bedingungen charakterisieren Zufallsexperimente?

Frage 3 von 5

Wann wird Ziehen mit Zurücklegen angewendet?

Frage 4 von 5

Was bedeutet Berücksichtigung der Reihenfolge bei Urnenmodellen?

Frage 5 von 5

Das Urnenmodell im Überblick

Urnenmodelle beschreiben in der Mathematik Zufallsexperimente.
Die Urne ist ein Gefäß, aus dem unterscheidbare Kugeln gezogen werden, ähnlich wie beispielsweise beim Lotto.
Es gibt vier verschiedene Arten von Urnenmodellen: Ziehen mit Zurücklegen und ohne Zurücklegen sowie Ziehen mit Berücksichtigung der Reihenfolge und ohne Berücksichtigung der Reihenfolge.

Quelle sofatutor.com

Urnenmodelle – Definition und Eigenschaften

Urnenmodelle sind eine Methode in der Mathematik, um Zufallsexperimente zu modellieren. In diesem Text werden die vier wichtigsten Urnenmodelle einfach erklärt.

Urnenmodelle als Zufallsexperimente

Als Urnenmodell werden in der Mathematik Modelle für Zufallsexperimente bezeichnet. Zur Veranschaulichung werden ganz verschiedene Zufallsexperimente mit dem Ziehen von Kugeln aus einer Urne verglichen. Die Kugeln sind voneinander unterscheidbar, z. B. indem sie mit den Zahlen $1$ , $2$ , $3$ usw. beschriftet sind. Unter einer Urne ist dabei einfach ein Gefäß zu verstehen, aus dem die Kugeln blind entnommen werden.

Aus der Urne wird eine Kugel nach der anderen gezogen. Die Anzahl der Kugeln wird in der Regel mit der Variable $n$ bezeichnet, die Anzahl der Ziehungen mit der Variable $k$ .

Die Kugeln werden so gezogen, dass bei der Ziehung die Zahl auf der Kugel nicht zu erkennen ist. Beim Ziehen aus der Urne handelt es sich um ein Zufallsexperiment, denn die Ziehung erfolgt zufällig, d. h., das Ergebnis ist nicht vorhersehbar. Die möglichen Ergebnisse der Ziehung sind vor der Ziehung bereits bekannt, denn die Anzahl der Kugeln und ihre Beschriftungen sind festgelegt. Außerdem ist die Ziehung unter den gleichen Bedingungen beliebig oft wiederholbar. Diese drei Bedingungen charakterisieren Zufallsexperimente.

Das Ziehen einer Kugel aus einer Urne mit $n$ Kugeln ist ein Laplace-Experiment. Das bedeutet, dass jedes Elementarereignis die gleiche Wahrscheinlichkeit hat. Die Wahrscheinlichkeit eines beliebigen Ereignisses $E$ lässt sich daher mit der folgenden Formel für Laplace-Experimente berechnen:
$P(E) = \dfrac{\text{{Anzahl der für }} E \text{{ günstigen Ergebnisse}}}{\text{{Anzahl aller möglichen Ergebnisse}}} = \dfrac{\vert E \vert}{\vert \Omega \vert}$
Hierbei bezeichnet $\Omega$ die Menge aller möglichen Ergebnisse des Zufallsexperiments.

Wie die Ergebnismenge $\Omega$ genau aussieht und wie viele Elemente $\Omega$ hat, hängt davon ab, welche Kugeln (Elementarereignisse) sich in der Urne befinden.

Wenn wir ein Zufallsexperiment als $k$ -faches Ziehen einer Kugel modellieren, dann müssen wir folgende Fälle unterscheiden:

Ziehen mit oder ohne Zurücklegen:
Wird die gezogene Kugel nach jedem Zug in die Urne zurückgelegt oder nicht?
Ziehen mit oder ohne Betrachtung der Reihenfolge:
Ist die Reihenfolge der Ergebnisse der einzelnen Züge relevant?

Aus der Kombination dieser beiden Kriterien ergeben sich die vier Urnenmodelle für Zufallsexperimente, die wir im Folgenden genauer betrachten.

Ziehen mit Zurücklegen mit Berücksichtigung der Reihenfolge

Beispiel 1

Im ersten Schritt wird eine Kugel gezogen und die Nummer der Kugel notiert. Die Kugel wird wieder in die Urne zurückgelegt. Im zweiten Schritt wird wieder eine Kugel gezogen und die Nummer hinter der ersten Nummer notiert. Danach wird die Kugel wieder in die Urne zurückgelegt. Auf diese Weise werden insgesamt $k$ Kugeln gezogen und die Zahlen der Kugeln notiert. Bei jeder einzelnen Ziehung befinden sich gleich viele Kugeln in der Urne, nämlich $n$ . Daher kann die Anzahl der gezogenen Kugeln $k$ beliebig groß gewählt werden.
Ein Ergebnis des Zufallsexperiments besteht aus den $k$ Zahlen der gezogenen Kugeln in der Reihenfolge der Ziehung.

Beispiel 2

Aus der Urne mit $n$ Kugeln wird zuerst eine Kugel gezogen. Für das Ergebnis des ersten Zugs gibt es also $n$ verschiedene Möglichkeiten. Die gezogene Kugel wird vor dem zweiten Zug in die Urne zurückgelegt. Für den zweiten Zug gibt es also wieder $n$ verschiedene Möglichkeiten. Die Anzahl der Kombinationsmöglichkeiten der Ergebnisse des ersten und zweiten Zuges ist $n^2$ . Denn jedes mögliche Ergebnis des ersten Zugs kann mit jedem möglichen Ergebnis des zweiten Zugs kombiniert werden. Ganz analog ist die Anzahl der möglichen Ergebnisse von $k$ Ziehungen $n^k$ .
In diesem Urnenmodell gilt also:
$\vert \Omega\vert = n^k$
Hierbei bezeichnet $\Omega$ die Ergebnismenge. Es handelt sich um ein Laplace-Experiment, daher gilt für die Wahrscheinlichkeit eines beliebigen Ergebnisses $\omega$ :
$P(\{\omega\}) = \dfrac{1}{n^k}$

Beispiel 3

Stell dir ein Zahlenschloss vor. Du hast die Kombination vergessen und willst das Schloss durch Ausprobieren öffnen. Wie groß ist die Wahrscheinlichkeit, dass du bei einem Versuch spontan die richtige Kombination errätst?

Das Raten der Kombination kannst du als Zufallsexperiment verstehen. Um das Zufallsexperiment durch ein Urnenmodell darzustellen, musst du überlegen, was den Kugeln in der Urne entspricht und was dem Ziehen einer Kugel entspricht: Auf jedem Ring des Zahlenschlosses stehen die gleichen Zahlen. Um eine Zahlenkombination zu raten, wählst du auf jedem Ring eine Zahl aus. Das Auswählen der Zahl auf einem Ring entspricht also dem Ziehen einer Kugel aus der Urne und die Zahlen auf jedem Ring entsprechen den Kugeln in der Urne. Du musst so viele Zahlen wählen, wie das Zahlenschloss Ringe hat, daher entspricht die Anzahl der Ringe der Anzahl der Ziehungen aus der Urne.
Hast du auf einem Ring eine bestimmte Zahl gewählt, kannst du die gleiche Zahl auf dem nächsten Ring noch einmal wählen. Die Auswahl der Zahlen auf den Ringen entspricht im Urnenmodell also dem Ziehen mit Zurücklegen. Bei der Zahlenkombination ist die Reihenfolge entscheidend, daher verwendest du das Urnenmodell mit Berücksichtigung der Reihenfolge.

Dein Zahlenschloss hat vier Ringe. Auf jedem Ring stehen sechs Zahlen oder Symbole. In dem Urnenmodell wählst du also $k=4$ und $n=6$ . Die Anzahl der möglichen Zahlenkombinationen in dem Urnenmodell Ziehen mit Zurücklegen und mit Berücksichtigung der Reihenfolge ist $n^k=6^4=1\,296$ . Bei deinem Zahlenschloss kannst du also $1\,296$ verschiedene Zahlenkombinationen einstellen. Bis du diese Kombinationen alle durchprobiert hast, bist du lange beschäftigt.

Entsprechend gering ist die Wahrscheinlichkeit, dass du bei einmaligem Raten die richtige Kombination triffst: $P(\{\omega\}) = \frac{1}{1\,296} \approx 0,\!00077 = 0,\!077\,\%$

Ziehen mit Zurücklegen ohne Berücksichtigung der Reihenfolge

Beispiel 1

Im ersten Schritt wird eine Kugel gezogen und die Nummer der Kugel notiert. Die Kugel wird wieder in die Urne zurückgelegt. Im zweiten Schritt wird wieder eine Kugel gezogen und die Nummer notiert. Danach wird die Kugel wieder in die Urne zurückgelegt. Auf diese Weise werden insgesamt $k$ Kugeln gezogen und die Zahlen der Kugeln notiert. Bei jeder einzelnen Ziehung befinden sich gleich viele Kugeln in der Urne, nämlich $n$ . Daher kann die Anzahl der gezogenen Kugeln $k$ beliebig groß gewählt werden.
Ein Ergebnis des Zufallsexperiments besteht aus den $k$ Zahlen der gezogenen Kugeln in beliebiger Reihenfolge. Die gezogenen Zahlen können also z. B. der Größe nach sortiert werden. In diesem Ergebnis können einzelne Zahlen mehrfach vorkommen, da jede Kugel nach der Ziehung wieder in die Urne zurückgelegt wird und somit später noch einmal gezogen werden kann.

Beispiel 2

Aus der Urne mit $n$ Kugeln werden nacheinander $k$ Kugeln gezogen. Dabei sind $n$ und $k$ unabhängig voneinander. Jede der Kugeln kann mehrfach gezogen werden. Die Vielfachheiten der gezogenen Zahlen liegen zwischen $1$ und $k$ . Diese Vielfachheiten können beliebige Werte annehmen, aber die Summe der Vielfachheiten ist $k$ . Daher ist die Vielfachheit der $k$ -ten gezogenen Kugel bereits festgelegt durch die Vielfachheiten der vorigen Kugeln. Die Vielfachheiten der ersten bis zur $(k-1)$ -ten gezogenen Zahl sind nicht festgelegt, sondern ebenso zufällig wie die Werte der gezogenen Kugeln selbst. Daher ist die Anzahl der wählbaren Parameter nicht $n$ , sondern $n+k-1$ . In der Summe sind die $n$ Werte der Kugeln und die $k$ Werte der Vielfachheiten zusammengefasst.
Die Anzahl der verschiedenen Ziehungen ohne Berücksichtigung der Reihenfolge ist in diesem Urnenmodell:
$\vert \Omega\vert = \displaystyle \binom{n+k-1}{k} = \dfrac{(n+k-1!)}{(k! \cdot (n-1)!)}$

Beispiel 3

In eine gute Hexensuppe gehören drei spezielle Zutaten. Die Reihenfolge, in der die Zutaten in die Suppe getan werden, spielt keine Rolle. Das Regal ist reichlich gefüllt, sodass jede Zutat mehrfach verwendet werden kann. Insgesamt stehen zehn der speziellen Hexensuppen-Zutaten zur Auswahl. Wie viele verschiedene Rezepte für Hexensuppe sind damit möglich? Und wie wahrscheinlich ist es, dass ein Hexenlehrling durch bloßes Raten die richtige Hexensuppe kocht?

Bei der Modellierung des Zufallesexperiments Hexensuppe wählst du das Urnenmodell mit Zurücklegen und ohne Berücksichtigung der Reihenfolge. Denn die Reihenfolge der Zutaten ist für die Suppe nicht relevant. Und da du jede Zutat mehrfach verwenden darfst, handelt es sich um Ziehen mit Zurücklegen. Die Zutaten im Regal entsprechen den Kugeln in der Urne, die Zutaten, die du für die Suppe auswählst, entsprechen den gezogenen Kugeln. Bei zehn Zutaten im Regal und drei Zutaten für die Hexensuppe ist also $n=10$ und $k=3$ .
Die Anzahl der verschiedenen Ziehungen mit Zurücklegen ohne Berücksichtigung der Reihenfolge ist die gesuchte Anzahl verschiedener möglicher Rezepte für die Hexensuppe. Mit der Formel für dieses Urnenmodell erhältst du $\binom{n+k-1}{k} = \binom{12}{3} = \frac{12 \cdot 11 \cdot 10}{3\cdot 2\cdot 1} =220$ verschiedene Rezepte für Hexensuppe. Die Wahrscheinlichkeit, dass der Hexenlehrling zufällig die richtige Suppe kocht, ist also $P(\{\omega\} = \frac{1}{220} = 0,\!00\overline{45} \approx 0,\!5\%$ .

Ziehen ohne Zurücklegen mit Berücksichtigung der Reihenfolge

Beispiel 1

Im ersten Schritt wird eine Kugel gezogen und die Nummer der Kugel notiert. Die Kugel wird nicht wieder in die Urne zurückgelegt. Im zweiten Schritt wird wieder eine Kugel gezogen und die Nummer hinter der ersten Nummer notiert. Danach wird auch die zweite Kugel nicht wieder in die Urne zurückgelegt. Auf die gleiche Weise werden insgesamt $k$ Kugeln gezogen und die Zahlen der Kugeln notiert. Bei jeder einzelnen Ziehung befindet sich eine Kugel weniger in der Urne als bei der vorigen Ziehung. Daher können in diesem Fall maximal $k = n$ Kugeln aus der Urne entnommen werden.
Ein Ergebnis des Zufallsexperiments besteht aus den $k$ Zahlen der gezogenen Kugeln in der Reihenfolge der Ziehung.

Beispiel 2

Aus der Urne mit $n$ Kugeln wird zuerst eine Kugel gezogen. Für das Ergebnis des ersten Zugs gibt es also $n$ verschiedene Möglichkeiten. Nach dem ersten Zug sind nur noch $n-1$ Kugeln in der Urne. Für das Ergebnis des zweiten Zugs gibt es also nur noch $n-1$ verschiedene Möglichkeiten. Die Anzahl der Kombinationsmöglichkeiten des ersten und zweiten Zugs beträgt $n \cdot (n-1)$ , denn jedes mögliche Ergebnis des ersten Zugs kann mit jedem möglichen Ergebnis des zweiten Zugs kombiniert werden. Bei $k$ Ziehungen erhält man als Anzahl der Möglichkeiten ein Produkt aus $k$ Faktoren. Jeder nächste Faktor ist um $1$ kleiner als der vorige und der erste Faktor ist $n$ . Der letzte Faktor ist dann $n-k+1$ .
In diesem Urnenmodell gilt also:
$\vert \Omega\vert = n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot (n-k+1) = \dfrac{n!}{(n-k)!}$
Da es sich auch hier um ein Laplace-Experiment handelt, erhalten wir für die Wahrscheinlichkeit eines Elementarereignisses $\omega$ :
$P(\{\omega\}) = \dfrac{(n-k)!}{n!}$

Als Spezialfall betrachten wir das Ziehen aller $n$ Kugeln ohne Zurücklegen und mit Berücksichtigung der Reihenfolge: In diesem Fall ist also $k=n$ . Die Anzahl der Ergebnisse dieses Zufallsexperiments ist $n \cdot (n-1) \cdot \ldots \cdot 2 \cdot 1 = n!$ .

Beispiel 3

Bei einem Fahrradrennen bekommen die drei ersten einen Preis. Jede Teilnehmerin oder jeder Teilnehmer bekommt eine Startnummer. Du möchtest eine Wette abschließen, welche Startnummern die ersten drei Plätze belegen. Da du die Teilnehmerinnen und Teilnehmer des Rennens und ihre sportlichen Leistungen nicht kennst, kannst du nur raten. Wie viele mögliche Platzierungen gibt es und wie groß ist die Wahrscheinlichkeit, dass du auf die richtige Platzierung setzt?

Das Raten der Platzierung kannst du als Zufallsexperiment verstehen. Für die Darstellung durch ein Urnenmodell musst du die Anzahl der Kugeln in der Urne und die Anzahl der Ziehungen identifizieren. Außerdem musst du klären, um welches Urnenmodell es sich handelt.
Beim Raten der Platzierung wählst du nacheinander die Startnummern der ersten drei Plätze aus. Da du drei Plätze besetzt, wählst du drei Startnummern. Die Anzahl der Ziehungen ist also $k=3$ . Die Anzahl der Kugeln in der Urne entspricht der Anzahl der vergebenen Startnummern bei diesem Rennen. Bei einem Rennen mit zehn Teilnehmerinnen oder Teilnehmern ist also $n=10$ . Hast du eine Startnummer für den ersten Platz gewählt, kannst du die gleiche Startnummer nicht auch für den zweiten oder dritten Platz wählen. Es handelt sich im Urnenmodell also um Ziehen ohne Zurücklegen. Die Reihenfolge ist bei der Platzierung entscheidend – es ist ein Unterschied, ob jemand einen ersten oder dritten Platz belegt. Daher verwendest du das Urnenmodell mit Berücksichtigung der Reihenfolge.
Die Anzahl verschiedener möglicher Platzierungen von $n=10$ Startnummern auf $k=3$ Plätze ist also $\frac{n!}{(n-k)!} = 10 \cdot 9 \cdot 8 = 720$ . Es gibt also $720$ verschiedene mögliche Belegungen der ersten drei Plätze. Die Wahrscheinlichkeit, die richtige Belegung zu raten, ist $P(\{\omega\}) = \frac{1}{720} \approx 0,\!0014 = 0,\!14\,\%$ .

Ziehen ohne Zurücklegen ohne Berücksichtigung der Reihenfolge

Beispiel 1

Im ersten Schritt wird eine Kugel gezogen und die Nummer der Kugel notiert. Die Kugel wird nicht wieder in die Urne zurückgelegt. Im zweiten Schritt wird wieder eine Kugel gezogen und die Nummer notiert. Danach wird auch die zweite Kugel nicht wieder in die Urne zurückgelegt. Auf die gleiche Weise werden insgesamt $k$ Kugeln gezogen und die Zahlen der Kugeln notiert. Bei jeder einzelnen Ziehung befindet sich eine Kugel weniger in der Urne als bei der vorigen Ziehung. Daher können in diesem Fall maximal $k = n$ Kugeln aus der Urne entnommen werden.
Ein Ergebnis des Zufallsexperiments besteht aus den $k$ Zahlen der gezogenen Kugeln in beliebiger Reihenfolge. Die gezogenen Zahlen können also z. B. der Größe nach sortiert werden.

Beispiel 2

Aus der Urne mit $n$ Kugeln werden wie zuvor nacheinander und ohne Zurücklegen $k$ Kugeln gezogen. Zunächst wird die Reihenfolge noch berücksichtigt. Die Anzahl dieser Ergebnisse ist nach dem vorigen Urnenmodell $\frac{n!}{(n-k)!}$ . In jedem solchen Ergebnis kommt keine der $k$ gezogenen Zahlen mehrfach vor.
Die Anzahl möglicher Anordnungen oder Umsortierungen der $k$ gezogenen Zahlen ist $k!$ – unabhängig davon, welche $k$ Zahlen genau gezogen wurden. Mit anderen Worten: Jede mögliche Auswahl von $k$ verschiedenen Zahlen kommt in dem Urnenmodell mit Berücksichtigung der Reihenfolge genau $k$ -mal vor, nämlich in $k$ verschiedenen Reihenfolgen. Die Anzahl der Möglichkeiten ohne Berücksichtigung der Reihenfolge erhalten wir demnach aus der Anzahl der Möglichkeiten mit Berücksichtigung der Reihenfolge, indem wir durch die Anzahl der Umsortierungen (Permutationen) dividieren.
Wir erhalten also:
$\vert \Omega\vert = \dfrac{n!}{(n-k)!} \cdot \dfrac{1}{k!} = \dfrac{n!}{k! \cdot (n-k)!} = \displaystyle \binom{n}{k}$

Beispiel 3

Das bekannteste Beispiel für dieses Urnenmodell ist ein Glücksspiel, bei dem sich $49$ Kugeln in einer Urne befinden, aus der $6$ Kugeln gezogen werden. Die Kugeln werden nicht zurückgelegt und die Reihenfolge der Ziehungen wird nicht berücksichtigt. Wie groß ist die Wahrscheinlichkeit, beim Lotto $6$ aus $49$ sechs Richtige zu erhalten?

Wir verwenden das Urnenmodell Ziehen ohne Zurücklegen ohne Berücksichtigung der Reihenfolge mit $n=49$ und $k=6$ . Die Anzahl der verschiedenen möglichen Ziehungen ist dann $\binom{n}{k} = \binom{49}{6} = \frac{49\cdot 48\cdot 47\cdot 46\cdot 45\cdot 44 \cdot 43}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}= 13\,983\,816$ . Die Wahrscheinlichkeit, mit einem Tippschein sechs Richtige zu treffen, ist $\frac{1}{13\,983\,816} \approx 0,\!000\,000\,07 = 0,\!000\,007\!\%$ .

Urnenmodelle – Formeln mit Herleitung

Die folgenden Formeln geben jeweils an, wie viele mögliche Ausgänge das Zufallsexperiment hat. Die Anzahl der möglichen Ausgänge ist das Gleiche wie die Anzahl der möglichen Ergebnisse, also die Anzahl $\vert \Omega\vert$ der Elemente der Ergebnismenge $\Omega$ . D

In den Formeln wird die Schreibweise der Fakultäten verwendet. Das Symbol $n!$ bezeichnet ein Produkt mit $n$ Faktoren. Der erste Faktor ist eine natürliche Zahl $n$ , jeder weitere Faktor ist um $1$ kleiner als der vorige. Es ist also $n!=n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot 2 \cdot 1$ . Beispielsweise ist $5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120$ und $7! = 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=5\,040$ . Außerdem wird verwendet, dass Brüche mit Fakultäten gut gekürzt werden können. Beispielsweise ist
$\dfrac{6!}{4!} = \dfrac{6 \cdot 5 \cdot \not{\!4} \cdot \not{\!3} \cdot \not{\!2} \cdot \not{\!1}}{\not{\!4} \cdot \not{\!3} \cdot \not{\!2} \cdot \not{\!1}} = \dfrac{6 \cdot 5}{1} = 30$
Allgemein gilt für Zahlen $n$ und $k$ mit $k\leq n$ :
$\dfrac{n!}{k!} = \dfrac{n \cdot (n-1) \cdot \ldots \cdot (k+2) \cdot (k+1) \cdot \not{\!k} \ldots \cdot \not{\!2} \cdot \not{\!1}}{\not{\!k} \cdot \ldots \cdot \not{\!2} \cdot\not{\!1}} = n \cdot (n-1) \cdot \ldots \cdot (k+1)$

Wir betrachten für alle vier Urnenmodelle eine Urne mit $n$ Kugeln, aus der nacheinander $k$ Kugeln gezogen werden. Dabei gilt:

Beim Ziehen ohne Zurücklegen ist stets 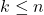$k \leq n$ , denn es können nicht mehr Kugeln gezogen werden, als in der Urne sind.
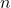Beim Ziehen mit Zurücklegen ist $k > n$ ebenfalls möglich. Denn in der Urne befinden sich bei jedem Zug $n$ Kugeln. Wir können also beliebig oft aus der Urne ziehen.

Formeln zu Urnenmodellen im Überblick

In der folgenden Tabelle findest du für alle vier Urnenmodelle die Anzahl der Ergebnisse bei der Ziehung von $k$ Kugeln aus $n$ im Überblick.

Ziehung $k$ aus $n$	Mit Zurücklegen	Ohne Zurücklegen
mit Reihenfolge	$n^k$	$\dfrac{n!}{(n-k)!}$
ohne Reihenfolge	$\displaystyle \binom{n+k-1}{n}$	$\displaystyle \binom{n}{k} = \frac{n!}{k!(n-k)!}$

Häufig gestellte Fragen zum Thema Urnenmodelle

Was ist ein Urnenmodell in Mathe?

Als Urnenmodell bezeichnen wir in der Mathematik Modelle für Zufallsexperimente. Zur Veranschaulichung werden ganz verschiedene Zufallsexperimente mit dem Ziehen von Kugeln aus einer Urne verglichen. Die Kugeln sind dabei unterscheidbar. Unter der Urne ist einfach ein Gefäß zu verstehen.

Welche Urnenmodelle gibt es?

Es gibt grundsätzlich vier verschiedene Urnenmodelle. Sie unterscheiden sich zum einen dadurch, ob die einzelnen Kugeln nach der Ziehung zurückgelegt werden oder nicht. Wir sprechen dann vom Ziehen mit Zurücklegen oder Ziehen ohne Zurücklegen. Zum anderen unterscheiden sich die einzelnen Urnenmodelle dadurch, ob die Reihenfolge der Ziehungen berücksichtigt wird oder nicht. Wir sprechen dann von Ziehen mit Berücksichtigung der Reihenfolge oder Ziehen ohne Berücksichtigung der Reihenfolge.

Was bedeutet Ziehen mit Zurücklegen?

Aus einer Urne werden mit Zahlen beschriftete Kugeln gezogen. Nach jeder Ziehung wird die Nummer der gezogenen Kugeln notiert. Vor der nächsten Ziehung wird die gezogene Kugel in die Urne zurückgelegt. Es befinden sich also bei jeder Ziehung gleich viele Kugeln in der Urne. In dem Ergebnis von mehreren Ziehungen kann also dieselbe Kugel mehrfach gezogen werden.

Wann benutzt man Ziehen mit Zurücklegen?

Ziehen mit Zurücklegen wird verwendet, wenn in den betrachteten Ergebnissen einzelne Merkmale mehrfach vorkommen können. Das ist z. B. bei Zahlenschlössern der Fall: Auf jedem Ring stehen die gleichen Zahlen. Jede Zahl kann mehrfach gewählt werden.

Was bedeutet Ziehen ohne Zurücklegen?

Beim Ziehen ohne Zurücklegen werden gezogene Kugeln nicht wieder in die Urne zurückgelegt. Bei jeder Ziehung ist also eine Kugel weniger in der Urne als bei der vorigen Ziehung. In dem Ergebnis aus mehreren Ziehungen kommt dieselbe Kugel daher nicht mehrfach vor. Ziehen ohne Zurücklegen verwendet man beispielsweise zur Modellierung von Glücksspielen wie Lotto oder zur Modellierung von Platzierungen bei Wettkämpfen, wo jede Person nur je einen Platz einnehmen kann.

Was bedeutet Berücksichtigung der Reihenfolge?

Berücksichtigung der Reihenfolge bedeutet, dass Ergebnisse aus mehreren Ziehungen danach unterschieden werden, in welcher Reihenfolge die Kugeln gezogen werden. Ziehst du zuerst eine $2$ und dann eine $6$ , erhältst du ein anderes Ergebnis, als wenn du zuerst die $6$ ziehst und danach die $2$ . Die Berücksichtigung der Reihenfolge ist beispielsweise bei der Platzierungen in Wettkämpfen wichtig: Es ist ein Unterschied, ob du auf dem zweiten oder auf dem sechsten Platz landest. Auch bei Zahlenkombinationen von Schlössern oder bei Codes ist die Reihenfolge der Zahlen und Buchstaben relevant und muss daher berücksichtigt werden.

Wie viele Kugeln sind in der Urne?

Die Anzahl der Kugeln in der Urne bezeichnet man in den meisten Urnenmodellen mit der Variable $n$ . Die Anzahl der Ziehungen wird üblicherweise mit der Variable $k$ bezeichnet. Man bezeichnet das Urnenmodell mit diesen Variablen auch als Ziehung von $k$ aus $n$ . Ein bekanntes Beispiel ist das Lotto $6$ aus $49$ : Aus den $n=49$ Kugeln in der Urne werden $k=6$ gezogen.

Wie viele Kugeln müssen der Urne mit Zurücklegen entnommen werden?

Die Anzahl Ziehungen wird in den meisten Urnenmodellen mit der Variable $k$ bezeichnet. Die Anzahl der Kugeln in der Urne trägt meistens die Bezeichnung $n$ . Man zieht dann $k$ aus $n$ Kugeln.

Wie hoch ist die Wahrscheinlichkeit, eine schwarze Kugel zu ziehen?

In Urnenmodellen mit verschiedenfarbigen Kugeln ist die Wahrscheinlichkeit, eine Kugel einer bestimmten Farbe zu ziehen, genauso groß wie der Anteil der Kugeln dieser Farbe an allen Kugeln in der Urne. Befinden sich in einer Urne insgesamt $10$ Kugeln, von denen $3$ schwarz sind und die anderen $7$ Kugeln eine oder verschiedene andere Farben haben, ist die Wahrscheinlichkeit, eine schwarze Kugel zu ziehen:
$\dfrac{3}{10}=0,\!3=30\,\%$