Geometrie: Oktaeder – Merkmale und Formeln

Ein Oktaeder ist ein regelmäßiger geometrischer Körper, der acht kongruente Dreiecke als Seitenflächen besitzt. Es entsteht, wenn zwei gleichseitige quadratische Pyramiden an ihrer Grundseite zusammengeklebt werden. 

Das Oktaeder gehört zu den fünf platonischen Körpern. Die fünf platonischen Körper sind das Tetraeder, der Würfel, das Oktaeder, das Dodekaeder und das Ikosaeder. Für platonische Körper gilt:

Ein Oktaeder besitzt:

• sechs Ecken,
• zwölf Kanten und
• acht Flächen.

Es gilt:

Die Kanten eines Oktaeders sind alle gleich lang und werden mit dem Buchstaben bezeichnet.

Das Oktaeder besitzt vielfältige Symmetrieeigenschaften. Es ist punktsymmetrisch zum Mittelpunkt. Zudem besitzt es einige Dreh- und Spiegelsymmetrien:

• Drei Drehachsen durch die gegenüberliegenden Ecken
• Vier Drehachsen durch die Mittelpunkte gegenüberliegender Flächen
• Sechs Drehachsen durch die Mittelpunkte gegenüberliegender Kanten
• Drei Symmetrieebenen durch je vier Ecken
• Sechs Symmetrieebenen durch je zwei Ecken und zwei Kantenmittelpunkte
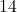• Drehspiegelungen

Die Formeln zur Berechnung verschiedener Größen des Oktaeders schauen wir uns an dem folgenden Beispiel an:

Das Oktaeder hat eine Kantenlänge von . Alle Kanten dieses Oktaeders besitzen die Länge .

Um das Volumen eines Oktaeders zu berechnen, nutzen wir die Formel:

Herleitung der Volumenformel für Oktaeder
Die Formel für das Volumen eines Oktaeders leitet sich aus dem Volumen einer gleichseitigen quadratischen Pyramide ab. Ein Oktaeder besteht aus zwei solchen Pyramiden. Es gilt also:

Dabei ist die Grundfläche der Pyramide und die Höhe. Die Grundfläche ist in diesem Fall ein Quadrat mit der Seitenlänge . Deshalb gilt:

Die Höhe der Pyramide bildet mit einer Außenkante und halben Diagonalen ein Dreieck.

Da es sich um ein rechtwinkliges Dreieck handelt, gilt für dieses Dreieck:

Für die Strecke gilt dabei:

Setzen wir das in die Formel ein und stellen diese nach um, erhalten wir für die Höhe der Pyramide die Formel:

Setzen wir beide Größen in die Formel ein und multiplizieren mit zwei, erhalten wir die Formel für das Volumen eines Oktaeders:

Beispiel

Um die Oberfläche eines Oktaeders zu berechnen, nutzen wir die Formel:

Herleitung der Oberflächenformel für Oktaeders
Das Oktaeder besteht aus acht gleichseitigen Dreiecken. Daher gilt für die Oberfläche des Oktaeders:

Für den Flächeninhalt gleichseitiger Dreiecke gilt:

Dabei ist die Seitenlänge des gleichseitigen Dreiecks.
Setzen wir das in die Formel für die Oberfläche des Oktaeders ein, dann erhalten wir die Formel:

Beispiel

Die Umkreiskugel ist die kleinste Kugel, die das komplette Oktaeder einschließt. Sie verläuft durch alle sechs Eckpunkte des Oktaeders. Ihren Radius berechnen wir mit der Formel:

Beispiel

Die Inkreiskugel ist die größte Kugel, die komplett in das Oktaeder hineinpasst. Sie berührt alle Seitenflächen von innen. Ihren Radius berechnen wir mit der Formel:

Beispiel

Die Raumdiagonale eines Oktaeders verbindet die beiden sich gegenüberliegenden Ecken. Ein Oktaeder besitzt drei gleich lange Raumdiagonalen. Ihre Länge berechnen wir mit der Formel:

Beispiel

In manchen Fällen ist nur die Oberfläche oder das Volumen, jedoch nicht die Seitenlänge bekannt. Wollen wir diese ermitteln, müssen wir die entsprechenden Formeln nach umstellen:

Beispiel
Betrachten wir ein Oktaeder mit einer Oberfläche von . Wie lang ist die Kante ?

Ein anderes Oktaeder hat das Volumen . Wie lang ist die Kante dieses Oktaeders?