Die e-Funktion ableiten – Regeln, Erklärung und Beispiele

Die e-Funktion ist eine spezielle mathematische Funktion mit der eulerschen Zahl als Basis. Ihre Ableitung entspricht wieder der e-Funktion und kann für allgemeine Exponentialfunktionen angewendet werden. Lerne mehr über Ableitungsregeln und praktische Beispiele!

Inhaltsverzeichnis zum Thema e-Funktion

Ableitung der e-Funktion im Überblick

  • Die e-Funktion e^x ist eine Exponentialfunktion mit der eulerschen Zahl e = 2,718… als Basis. Man nennt sie auch natürliche Exponentialfunktion.

  • Die Ableitung der e-Funktion ist wieder die e-Funktion.

  • Können wir die natürliche Exponentialfunktion ableiten, lässt sich damit jede beliebige Exponentialfunktion ableiten.

e-Funktion ableiten: Lernvideo

Quelle sofatutor.com

Bildergalerie zum Thema e-Funktion ableiten

e-Funktion
e-Funktion
e-Funktione-Funktion ableitenFaktorregel und ProduktregelFaktorregel und ProduktregelKettenregel für e-FunktionKettenregel für e-Funktione Funktion ableitenZusammengesetzte e-Funktionen ableiten

e-Funktion ableiten

Die e-Funktion e^x ist eine besondere Funktion in Mathe. Das gilt auch für das Ableiten der e-Funktion. Die e-Funktion ergibt abgeleitet wieder die e-Funktion, es gilt also:

(e^x)^\prime = e^x

e-Funktion ableiten – Herleitung der Formel

Die Ableitung der e-Funktion kann mithilfe des Differenzialquotienten bestimmt werden:

\begin f^\prime (x) &= \lim\limits_ \dfrac\\ &= \lim\limits_ \dfrac\\ &= \lim\limits_ \dfrac\\ &= e^x\cdot \lim\limits_ \dfrac\\ &=e^x \end

Der letzte Schritt in der Rechnung gilt, weil die eulersche Zahl so definiert ist, dass gilt:

\lim\limits_ \dfrac = 1

Damit gilt:

(e^x)^\prime = e^x

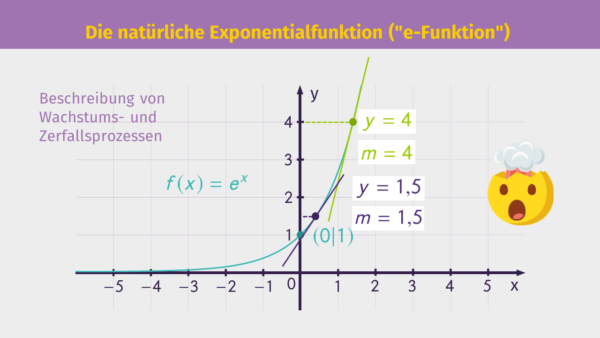
Diese Eigenschaft lässt sich auch nachvollziehen, wenn die e-Funktion grafisch abgeleitet wird. Dazu zeichnen wir Tangenten an die Funktionsgraphen und bestimmen ihre Steigung. Dabei stellen wir fest, dass an jeder Stelle des Graphen der e-Funktion der dortige Funktionswert genau der Tangentensteigung und somit der Steigung des Graphen an dieser Stelle entspricht.

e-Funktion grafisch ableiten

Zusammengesetzte Funktionen mit e-Funktionen ableiten – Beispiele

Oft taucht die e-Funktion in zusammengesetzten Funktionen auf. Um diese abzuleiten, werden weitere Ableitungsregeln, wie die Produkt- oder die Kettenregel, benötigt.
Im Folgenden schauen wir uns verschiedene Beispiele an.

Beschreibung Rechnung Erklärung
e-Funktion mit Vorfaktor ableiten
negative e-Funktion ableiten		 f(x) =5\cdot e^x
f^\prime(x) = 5\cdot e^x
f(x) =-e^x = (-1)\cdot e^x
f^\prime(x) = (-1)\cdot e^x=-e^x		 Die Faktorregel besagt, dass beim Ableiten der Vorfaktor bestehen bleibt, das gilt auch, wenn dieser negativ ist.
verkettete Funktion mit einer e-Funktion ableiten f(x) = e^{2x+5}
f^\prime(x) = e^{2x+5}\cdot(2x+5)^\prime = 2\cdot e^{2x+5}		 Die Funktion ist eine Verkettung aus u(x) = e^x und v(x) = 2x+5. Mithilfe der Kettenregel kann diese Funktion mit e-Funktion abgeleitet werden.
zusammengesetzte Funktion mit einer e-Funktion ableiten f(x) = e^x\cdot(x^2+3)
f^\prime (x) = e^x\cdot(x^2+3) + e^x\cdot2x = e^x\cdot(x^2+2x+3)		 Beim Ableiten dieser zusammengesetzten Funktion mit e-Funktion wird die Produktregel benötigt.
e-Funktion im Nenner ableiten f(x) = \frac{1}{e^x} = e^{-x}
f^\prime (x) = (-1)\cdot e^{-x} = -\frac{1}{e^x}		 Mithilfe der Potenzregel lässt sich die Funktion umformen, sodass die Kettenregel angewendet werden kann.

Exponentialfunktionen mit beliebiger Basis ableiten

Mithilfe der Ableitung der e-Funktion und der Kettenregel kann auch eine allgemeine Exponentialfunktion abgeleitet werden. Eine Exponentialfunktion f(x) = a^x mit der Basis a\neq0 kann umgeschrieben werden in:

f(x) = a^x = e^

Diese Eigenschaft liefert in Verbindung mit der Kettenregel die Ableitung:

\begin f^\prime (x) &= (a^x)^\prime\ &= \left(e^\right)^\prime\ &= \ln(a)\cdot e^\ &=\ln(a)\cdot a^x \end

Zusammengefasst lautet die Ableitung zu f(x)=a^x mit a\neq0 also:

f^\prime(x)=\ln(a)\cdot a^x

Häufig gestellte Fragen zum Thema e-Funktion ableiten

Die e-Funktion e^x ergibt abgeleitet wieder die e-Funktion. Wenn die e-Funktion mit anderen Funktionen verknüpft ist, müssen Ableitungsregeln wie die Ketten- oder die Produktregel beachtet werden.

Die Zahl e ist beim Ableiten wie eine Konstante zu behandeln. Tritt allerdings die e-Funktion auf, also f(x)=e^x, lautet die Ableitung:

f^\prime (x) = e^x

Mit dem Differenzialquotienten lässt sich nachrechnen, dass die Ableitung der e-Funktion wieder die e-Funktion ist.

Die Ableitung der Funktion f mit f(x) = e^x lautet:

f^\prime(x) = e^x

Wenn ein Funktionsterm aus einer e-Funktion multipliziert mit einem Term in Klammern besteht, handelt es sich um eine zusammengesetzte Funktion. Hier muss die Produktregel berücksichtigt werden.

Beim Ableiten der e-Funktion mit komplexen Exponenten muss die Kettenregel berücksichtigt werden.

Super! Das Thema: kannst du schon! Teile deine Learnings und Fragen mit der Community!

Alle Artikel aus dem Fach Mathematik