Kreis und Kreisumfang

Ein Kreis besteht aus einem Mittelpunkt, einem Radius und einem Durchmesser. Mit der Kreiszahl Pi kannst du den Kreisumfang und die Fläche berechnen. Entdecke, wie du diese Werte mithilfe von Radius oder Durchmesser ermittelst. Interessiert? Dies und vieles mehr findest du im folgenden Text!

Inhaltsverzeichnis zum Thema Kreis und Kreisumfang

Kreis und Kreisumfang im Überblick
Was ist ein Kreis und ein Kreisumfang?
Kreisumfang berechnen
Kreisfläche berechnen
Halbkreis
Kreisumfang und Kreisfläche berechnen – Beispiel
Vom Kreisumfang zum Durchmesser
Kreisumfang und Flächeninhalt berechnen – Zusammenfassung
Häufig gestellte Fragen zum Thema Kreis und Kreisumfang

Kreis und Kreisumfang im Überblick

Der Radius $r$ eines Kreises ist der Abstand von Mittelpunkt und Kreislinie.
Der Durchmesser $d$ ist genau doppelt so groß wie der Radius: $d = 2r$ .
Die Formel für den Kreisumfang lautet: $U= 2\pi \cdot r = \pi \cdot d$ .

Quelle sofatutor.com

Was ist ein Kreis und ein Kreisumfang?

Ein Kreis ist die Linie, auf der alle Punkte mit gleichem Abstand zum Mittelpunkt $M$ liegen.

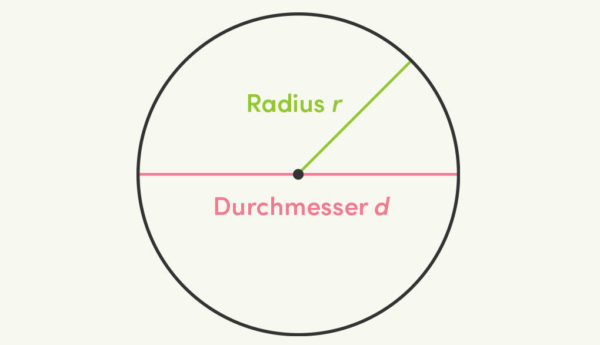
Der Abstand vom Mittelpunkt zum Kreis wird als Radius $r$ bezeichnet. Der größte Abstand von zwei Punkten auf dem Kreis wird Durchmesser $d$ genannt. Er läuft durch den Mittelpunkt und ist doppelt so groß wie der Radius: $d=2r$ .
Die Länge der Kreislinie wird Umfang $U$ genannt. Der Flächeninhalt $A$ ist die Fläche, die von der Kreislinie eingeschlossen wird.

Kreisumfang berechnen

Um den Umfang eines Kreises mithilfe des Radius zu berechnen, gibt es folgende Formel:
$U= 2\pi \cdot r$
Die Kreiszahl $\pi \approx 3,\!14$ ist eine Konstante mit unendlich vielen Nachkommastellen.
Wir wissen, dass der Durchmesser doppelt so groß ist wie der Radius, also $d=2r$ . Deshalb kann diese Kreisumfangsformel auch als Formel mit dem Durchmesser statt des Radius geschrieben werden:
$U= \pi \cdot d$

Kreisfläche berechnen

Die Formel für den Flächeninhalt eines Kreises lautet:
$A = \pi \cdot r^2$
Wie der Umfang kann auch der Flächeninhalt mithilfe des Durchmessers berechnet werden, da die Beziehung zwischen Radius und Durchmesser bekannt ist. Wird in obige Formel für die Fläche $d= \frac{r}{2}$ eingesetzt, ergibt sich:
$A = \pi \dfrac{d^2}{4}$

Halbkreis

Ein Halbkreis ist, wie der Name schon sagt, ein halber Kreis.
Somit gilt sowohl für den Flächeninhalt als auch den Umfang des Halbkreises, dass dieser jeweils genau die Hälfte des ganzen Kreises ist. Die entsprechenden Formeln, um die Fläche und den Umfang des Halbkreises zu berechnen, lauten also:
Umfang Halbkreis:
$U_H = \dfrac{1}{2}\cdot 2\pi \cdot r = \pi \cdot r = \dfrac{1}{2}\pi \cdot d$
Fläche Halbkreis:
$A_H = \dfrac{1}{2}\cdot \pi \cdot r^2 = \dfrac{1}{2}\cdot \pi \dfrac{d^2}{4} = \pi \dfrac{d^2}{8}$

Kreisumfang und Kreisfläche berechnen – Beispiel

Nun wollen wir uns einmal die Umfangsberechnung eines Kreises sowie die Flächenberechnung an einem Beispiel anschauen:
Gegeben ist ein Kreis mit Radius $r = 3~\text{cm}$ . Wie groß ist der Umfang und der Flächeninhalt des Kreises?
Dazu nutzen wir die obigen Formeln für den Kreis.
Den Umfang des Kreises berechnen wir mit der folgenden Formel:
$U = 2\pi \cdot r = 2\pi \cdot 3~\text{cm} \approx 18,\!85~\text{cm}$
Die Kreisfläche berechnen wir entsprechend:
$A = \pi \cdot r^2 = \pi \cdot (3 ~\text{cm})^2 \approx 28,\!27~\text{cm}^2$

Wäre hingegen der Durchmesser $d=6~\text{cm}$ gegeben, kannst du diesen zunächst durch 2 teilen, um den Radius zu erhalten und dann in die Formeln einzusetzen, oder du setzt direkt den Durchmesser $d$ in die Kreisformeln für Umfang und Fläche mit dem Durchmesser ein:
$U= \pi \cdot d = \pi \cdot 6~\text{cm} \approx 18,\!85~\text{cm}$
$A = \pi \frac{d^2}{4} = \pi \frac{( 6~\text{cm})^2}{4} \approx 28,\!27~\text{cm}^2$
Wie zu erwarten erhältst du die gleichen Werte.

Vom Kreisumfang zum Durchmesser

Möchtest du vom Kreisumfang auf den Durchmesser umrechnen, musst du die Formel für den Kreisumfang umstellen, indem du durch $\pi$ teilst:
$\begin{array}{rccc} & U & = & \pi \cdot d \\ \Leftrightarrow & d &= & \dfrac{U}{\pi} \end{array}$
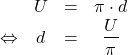
Hier setzt du nun den gegebenen Umfang ein.

Kreisumfang und Flächeninhalt berechnen – Zusammenfassung

Um den Umfang oder den Flächeninhalt eines Kreises zu berechnen, benötigst du den Radius $r$ oder den Durchmesser $d$ , die Zahl $\pi$ sowie zwei Formeln für den Kreis.
Die folgende Tabelle fasst die Formeln zusammen, die benötigt werden, um diese beiden Größen von Kreisen zu berechnen:

Umfang $U$	Flächeninhalt $A$
$U= 2\pi \cdot r$	$A = \pi \cdot r^2$
$U= \pi \cdot d$	$A = \pi \dfrac{d^2}{4}$

Häufig gestellte Fragen zum Thema Kreis und Kreisumfang

Was versteht man unter Umfang?

Der Umfang eines Kreises ist die Länge der Kreislinie. Die Kreislinie wiederum ist die Linie, auf der alle Punkte den gleichen Abstand $r$ vom Mittelpunkt haben.

Wie berechnet man den Umfang eines Kreises?

Den Umfang eines Kreises berechnest du mithilfe des Radius $r$ oder des Durchmessers $d=2r$ und der Zahl $\pi$ mit der Formel
$U = 2\pi \cdot r = \pi \cdot d$

Wie berechnet man den Umfang eines Kreises mit dem Durchmesser?

Um den Kreisumfang mit dem Durchmesser zu berechnen, nutzt du folgende Formel:
$U = \pi \cdot d$

Wie berechnet man den Radius mit dem Umfang?

Für den Kreisumfang gilt die Formel $U = 2\pi \cdot r$ . Hast du den Umfang $U$ gegeben und möchtest den Radius $r$ berechnen, stellst du die Formel nach $r$ um, indem du beide Seiten durch $2\pi$ teilst:
$r= \dfrac{U}{2\pi}$