Integral und Integralrechnung – Erklärung

Lerne, wie Integralrechnung funktioniert und wie du den Flächeninhalt zwischen einem Funktionsgraphen und der x-Achse berechnest. Bilden einer Stammfunktion, unbestimmtes und bestimmtes Integral, Integrationsregeln und Flächenberechnung zwischen Funktionen werden erklärt. Bereit zu verstehen? Dies und mehr im folgenden Text!

Inhaltsverzeichnis zum Thema Integral

Das Integral im Überblick
Integralrechnung – einfach erklärt
Stammfunktion
Stammfunktionen von Potenzfunktionen bilden
Integrale berechnen – einfach erklärt
Unbestimmtes Integral berechnen
Bestimmtes Integral berechnen
Integrationsregeln
Potenzregel
Faktorregel
Summenregel und Differenzenregel
Vertauschen der Integrationsgrenzen
Integralrechnung – Flächenberechnung
Fläche zwischen dem Graphen einer Funktion und der $x$ -Achse
Flächeninhalt zwischen zwei Funktionen
Integralrechnung – Anwendungsaufgaben
Häufig gestellte Fragen zum Thema Integral

Das Integral im Überblick

Mithilfe von Integralen lässt sich der Flächeninhalt berechnen, den ein Funktionsgraph mit der $x$ -Achse einschließt.
Dazu wird zunächst die sogenannte Stammfunktion $F(x)$ gebildet. Für diese gilt:
$F^\prime (x) = f(x)$
Das unbestimmte Integral umfasst alle Stammfunktionen einer Funktion $f(x)$ :
$\displaystyle \int f(x) ~\text{d}x = F(x) + c$ mit $c \in \mathbb{R}$
Für das bestimmte Integral gilt der Hauptsatz der Differenzial- und Integralrechnung:
$\displaystyle \int \limits_{a}^{b} f(x) ~\text{d}x = \Bigl[ F(x) \Bigr]_a^b = F(b) - F(a)$

Quelle sofatutor.com

Integralrechnung – einfach erklärt

Das Integral und die damit verbundene Integralrechnung helfen uns dabei, die Fläche zwischen dem Graphen einer Funktion und der $x$ -Achse zu berechnen. Um diesen Flächeninhalt zu ermitteln, muss zunächst die sogenannte Stammfunktion der Funktion gebildet werden.

Stammfunktion

Das Bilden einer Stammfunktion wird umgangssprachlich auch Aufleiten genannt, da es quasi das Gegenteil vom Ableiten einer Funktion ist. Die mathematisch korrekte Bezeichnung ist Integration. Leiten wir eine Stammfunktion $F(x)$ ab, erhalten wir die Funktion $f(x)$ . Es gilt also:

$F^\prime (x) = f(x)$

Beispiel
$f(x) = 3x^2 \quad \Rightarrow \quad F(x) = x^3$

Achtung: Da beim Ableiten Konstanten wegfallen, wird beim unbestimmten Integral $+~c$ mit $c \in \mathbb{R}$ ergänzt. Für jeden Wert von $c$ ergibt sich eine Stammfunktion, z. B. $x^3$ für $c = 0$ . Das unbestimmte Integral beschreibt die Summe aller Stammfunktionen in der Form $F(x) + c$ :

$\displaystyle \int 3x^2 ~\text{d}x = x^3 + c$ mit $c \in \mathbb{R}$

Stammfunktionen von Potenzfunktionen bilden

Besonders einfach ist das Bilden der Stammfunktionen von Potenzfunktionen. Dabei gehst du für $x^n$ folgendermaßen vor:

Schritt 1: Exponenten um eins erhöhen

$x^n ~\rightarrow~ x^{n~+~1$

Schritt 2: Bruch $\frac{1}{\text{neuer Exponent}}$ vor die Potenz schreiben

$\dfrac{1}{n+1} \cdot x^{n~+~1}$

Beispiel:

$\displaystyle \int x^5 ~\text{d}x = \dfrac{1}{5+1}\cdot x^{5+1} + c = \dfrac{1}{6}\,x^6 + c$ mit $c \in \mathbb{R}$

Integrale berechnen – einfach erklärt

Die Stammfunktionen von Funktionen können mithilfe von Integralen berechnet werden. Die mathematische Schreibweise für Integrale ist:

$\displaystyle \int f(x) ~\text{d}x$

Dabei ist:

$\int$ : Integrationszeichen – steht immer vor der Funktion, von der die Stammfunktion gebildet werden soll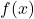
$f(x)$ : der Integrand
$dx$ : Differenzial – muss immer hinter dem Integranden stehen
$x$ : Integrationsvariable

Wir unterscheiden das unbestimmte und das bestimmte Integral.

Unbestimmtes Integral berechnen

Das unbestimmte Integral gibt die Gesamtheit aller Stammfunktionen einer Funktion an. Die Schreibweise für das unbestimmte Integral ist:

$\displaystyle \int f(x) ~\text{d}x = F(x) + c$ mit $c \in \mathbb{R}$

Dabei ist:

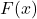$F(x)$ : eine Stammfunktion von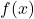 $f(x)$
$c$ : die Integrationskonstante

Beispiel unbestimmtes Integral:

$\displaystyle \int 3x^2 ~\text{d}x = x^3 + c$ mit $c \in \mathbb{R}$

Bestimmtes Integral berechnen

Das bestimmte Integral besitzt im Gegensatz zum unbestimmten Integral Grenzen, die sogenannten Integrationsgrenzen $a$ und $b$ . Soll mit dem Integral die Fläche zwischen dem Funktionsgraphen und der $x$ -Achse in einem bestimmten Intervall berechnet werden, dann setzen wir die Intervallgrenzen für $a$ und $b$ ein.
Das bestimmte Integral lässt sich mit der folgenden Formel berechnen:

$\displaystyle \int \limits_{a}^{b} f(x) ~\text{d}x = \Bigl[ F(x) \Bigr]_a^b = F(b) - F(a)$

Diese Formel wird auch als Hauptsatz der Integralrechnung bezeichnet.

Um ein Integral mit Integrationsgrenzen zu bestimmen, gehen wir folgendermaßen vor:

Schritt 1: Stammfunktion berechnen und in eckige Klammern setzen
Schritt 2: Integrationsgrenzen $a$ und $b$ in die Stammfunktion einsetzen
Schritt 3: $F(a)$ von $F(b)$ abziehen

Bestimmtes Integral ausrechnen – Beispiel:
Betrachten wir die Funktion $f(x) = 3x^2$ im Intervall $[0; 1]$ .

$\displaystyle \int \limits_{0}^{1} 3x^2 ~\text{d}x = \Bigl[ x^3 \Bigr]_0^1 = 1^3 - 0^3 = 1$

Dieses Integral gibt den Flächeninhalt zwischen dem Graphen der Funktion $f(x) = 3x^2$ und der $x$ -Achse im Intervall $[0; 1]$ an.

Integrationsregeln

Beim Rechnen mit Integralen müssen bestimmte Regeln, die sogenannten Integrationsregeln, beachtet werden.

Potenzregel

Die Potenzregel gibt die Vorschrift zum Integrieren von Potenzfunktionen an.

$\displaystyle \int x^n ~\text{d}x = \dfrac{1}{n+1} \cdot x^{n+1} + c$ mit $c \in \mathbb{R}$

Beispiel:
$\displaystyle \int x^4 ~\text{d}x = \dfrac{1}{5} \cdot x^{5} + c$ mit $c \in \mathbb{R}$

Faktorregel

Steht vor der Funktion ein Faktor $k$ , kann dieser einfach vor das Integral gezogen werden.

$\displaystyle \int k \cdot f(x) ~\text{d}x = k \cdot F(x) + c$ mit $c \in \mathbb{R}$

Beispiel:
$\displaystyle \int 2x^4 ~\text{d}x = 2 \cdot \int x^4 ~\text{d}x = 2 \cdot \dfrac{1}{5} \cdot x^{5} + c = \dfrac{2}{5} x^5 + c$ mit $c \in \mathbb{R}$

Summenregel und Differenzenregel

Steht im Integral eine Summe, können die Summanden einzeln integriert werden.

$\displaystyle \int f(x) + g(x) ~\text{d}x = \int f(x) ~\text{d}x + \int g(x) ~\text{d}x$

Beispiel:
$\displaystyle \int x^3 + x^4 ~\text{d}x = \int x^3 ~\text{d}x + \int x^4 ~\text{d}x = \dfrac{1}{4} \cdot x^4 + \dfrac{1}{5} \cdot x^5 + c$ mit $c \in \mathbb{R}$

Das Gleiche gilt für Differenzen:

$\displaystyle \int f(x) - g(x) ~\text{d}x = \int f(x) ~\text{d}x - \int g(x) ~\text{d}x$

Beispiel:
$\displaystyle \int 2x - x^4 ~\text{d}x = \int 2x ~\text{d}x - \int x^4 ~\text{d}x = x^2 - \dfrac{1}{5} x^5 + c$ mit $c \in \mathbb{R}$

Vertauschen der Integrationsgrenzen

Werden die Integrationsgrenzen getauscht, ändert sich das Vorzeichen des Integrals:

$\displaystyle \int \limits_{b}^{a} f(x) ~\text{d}x = - \int \limits_{a}^{b} f(x) ~\text{d}x$

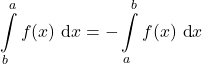
Beispiel:
$\displaystyle \int \limits_{0}^{1} 3x^2 ~\text{d}x = \Bigl[ x^3 \Bigr]_0^1 = 1^3 - 0^3 = 1$

$\displaystyle \int \limits_{1}^{0} 3x^2 ~\text{d}x = \Bigl[ x^3 \Bigr]_1^0 = 0^3 - 1^3 = -1$

Integralrechnung – Flächenberechnung

Wir nutzen die Integralrechnung, um den Flächeninhalt zwischen dem Graphen einer Funktion und der $x$ -Achse in einem Intervall zu berechnen. Aber auch der Flächeninhalt zwischen zwei Graphen lässt sich mithilfe von Integralen bestimmen.
Der Flächeninhalt ist nur dann positiv, wenn sich der Flächenabschnitt oberhalb der $x$ -Achse befindet. Liegt er unterhalb der $x$ -Achse, erhalten wir einen negativen Wert. Der Betrag dieses Werts ergibt dann den Flächeninhalt. Das Integral stellt im Allgemeinen nur eine Flächenbilanz dar. Das bedeutet, es gibt die Differenz zwischen der Fläche oberhalb und unterhalb der $x$ -Achse an. Um den wahren Flächeninhalt zu berechnen, müssen gegebenenfalls mehrere Abschnitte berechnet und betragsmäßig addiert werden.

Fläche zwischen dem Graphen einer Funktion und der $x$ -Achse

Ist das Intervall vorgegeben, muss lediglich das bestimmte Integral berechnet werden und wir erhalten den Flächeninhalt, den der Graph einer Funktion und die $x$ -Achse in diesem Intervall einschließen.
Funktionen mit mehreren Nullstellen schließen mit der $x$ -Achse eine Fläche zwischen den Nullstellen ein. Um den Flächeninhalt der eingeschlossenen Fläche zu berechnen, gehen wir folgendermaßen vor:

Schritt 1: Nullstellen der Funktion berechnen
Schritt 2: Bestimmtes Integral aufstellen, die Nullstellen bilden dabei die Integrationsgrenzen.
Schritt 3: Bestimmtes Integral berechnen

Hat deine Funktion mehr als zwei Nullstellen, müssen mehrere Integrale berechnet werden. Hat die Funktion zum Beispiel Nullstellen bei $0$ , $2$ und $4$ , dann muss ein Integral für das Intervall $[0; 2]$ und ein Integral für das Intervall $[2; 4]$ berechnet werden. Für den gesamten Flächeninhalt werden dann die Beträge der Teilintegrale addiert.

Flächenberechnung mit einem Integral – Beispiel
Betrachten wir die Funktion
$f(x) = - \dfrac{x^2}{2} + x$

Zunächst müssen wir die Nullstellen der Funktion berechnen.

$0 = - \dfrac{x^2}{2} + x$
$0 = x \cdot \left( -\dfrac{1}{2} x + 1 \right)$

$\Rightarrow \quad x_1 = 0 ; ~x_2 = 2$

Nun können wir das bestimmte Integral aufstellen. Durch das Anwenden der Integrationsregeln können wir das Integral vereinfachen.

$\displaystyle \int \limits_{0}^{2} - \dfrac{x^2}{2} + x ~\text{d}x = -\dfrac{1}{2} \int \limits_{0}^{2} x^2 ~\text{d}x + \int \limits_{0}^{2} x ~\text{d}x$

Nun können wir die Integrale lösen.

$\displaystyle -\dfrac{1}{2} \int \limits_{0}^{2} x^2 ~\text{d}x + \int \limits_{0}^{2} x ~\text{d}x = - \dfrac{1}{2} \cdot \left[\dfrac{1}{3} x^3 \right]_{0}^{2} + \left[ \dfrac{1}{2} x^2 \right]_{0}^{2}$

Durch Einsetzen der Integrationsgrenzen erhalten wir den Flächeninhalt:

$- \dfrac{1}{2} \cdot \left[\dfrac{1}{3} x^3 \right]_{0}^{2} + \left[ \dfrac{1}{2} x^2 \right]_{0}^{2}$

$\quad = - \dfrac{1}{2} \cdot \left( \dfrac{1}{3} \cdot 2^3 - \dfrac{1}{3} \cdot 0^3 \right) + \left( \dfrac{1}{2} \cdot 2^2 - \dfrac{1}{2} \cdot 0^2 \right)$

$\quad = - \dfrac{1}{2} \cdot \dfrac{8}{3} + 2$

$\quad = - \dfrac{4}{3} + 2 = \dfrac{2}{3}$

Die Fläche beträgt $\frac{2}{3}$ Flächeneinheiten ( $\text{FE}$ ).

Flächeninhalt zwischen zwei Funktionen

Mithilfe von Integralen lassen sich auch Flächen zwischen zwei Graphen bestimmen. Für die Flächenberechnung zwischen zwei Graphen gehst du folgendermaßen vor:

Schritt 1: Schnittpunkte der beiden Funktionen $f(x)$ und $g(x)$ berechnen
Schritt 2: Integral von $g(x)-f(x)$ aufstellen, wobei die $x$ -Werte der Schnittpunkte die Integrationsgrenzen sind
Schritt 3: Bestimmtes Integral berechnen

Integralrechnung – Beispiel
Betrachten wir die Funktionen $f(x) = x^2$ und $g(x) = x + 0,\!75$

Zunächst müssen wir die Schnittpunkte der beiden Funktionen bestimmen. Dazu setzen wir die Funktionsterme gleich und lösen nach $x$ auf.

$\begin{array}{rcll} f(x) & = & g(x) &\\ x^2 & = & x + 0,\!75 & \vert - x^2 \\ 0 & = & -x^2 + x + 0,\!75 & \\ \end{array}$

Durch Einsetzen in die Mitternachtsformel erhalten wir die Schnittpunkte $x_1 = -0,\!5$ und $x_2 = 1,\!5$ . Diese bilden die Integrationsgrenzen $a$ und $b$ .

$\displaystyle \int \limits_{-0,5}^{1,5} x + 0,\!75 - x^2 ~\text{d}x$
$\quad \displaystyle = \int \limits_{-0,5}^{1,5} -x^2 + x + 0,\!75 ~\text{d}x$
$\quad = \left[ - \dfrac{1}{3}x^3 + \dfrac{1}{2}x^2 + 0,\!75x \right]_{-0,5}^{1,5}$

Durch das Einsetzen der Integrationsgrenzen erhalten wir den Flächeninhalt:

$\left[ - \dfrac{1}{3}x^3 + \dfrac{1}{2}x^2 + 0,\!75x \right]_{-0,5}^{1,5}$

$\quad = \left(- \dfrac{1}{3} \cdot (1,\!5)^3 + \dfrac{1}{2} \cdot (1,\!5)^2 + 0,\!75 \cdot 1,\!5 \right) - \left( - \dfrac{1}{3} \cdot (-0,\!5)^3 + \dfrac{1}{2} \cdot (-0,\!5)^2 + 0,\!75 \cdot (-0,\!5) \right)$

$\quad = \left( -\dfrac{9}{8} + \dfrac{9}{8} + \dfrac{9}{8} \right) - \left(\dfrac{1}{24} + \dfrac{1}{8} - \dfrac{3}{8} \right)$

$\quad = \dfrac{4}{3}$

Die von $f(x)$ und $g(x)$ eingeschlossene Fläche beträgt $\frac{4}{3}~\text{FE}$ .

Integralrechnung – Anwendungsaufgaben

Aufgabe 1
Wie groß ist die Fläche zwischen der Funktion $f(x) = \dfrac{1}{3}x + 2$ und der $x$ -Achse im Intervall $[0; 4]$ ?

Lösung Aufgabe 1
Zunächst stellen wir das Integral mit den entsprechenden Integrationsgrenzen auf.

$\displaystyle \int \limits_{0}^{4} \dfrac{1}{3}x + 2 ~\text{d}x = \dfrac{1}{3} \cdot \int \limits_{0}^{4} x ~\text{d}x + \int \limits_{0}^{4} 2 ~\text{d}x$

Im Anschluss können wir die Integrale lösen und die Integrationsgrenzen in die Stammfunktionen einsetzen:

$\displaystyle \dfrac{1}{3} \cdot \int \limits_{0}^{4} x ~\text{d}x + \int \limits_{0}^{4} 2 ~\text{d}x$

$\quad =\dfrac{1}{3} \cdot \left[ \dfrac{1}{2}x^2 \right]_0^4 + \Bigl[2x \Bigr]_0^4$

$\quad = \dfrac{1}{6} \cdot (4^2 - 0^2) + (2 \cdot 4 - 2 \cdot 0)$

$\quad = \dfrac{1}{6} \cdot 16 + 8 = \dfrac{8}{3} + 8 = \dfrac{32}{3}$

Die Funktion $f(x)$ und die $x$ -Achse schließen im Intervall $[0; 4]$ eine Fläche von $\frac{32}{3}~\text{FE}$ ein.

Aufgabe 2
Wie groß ist die Fläche zwischen den Graphen der Funktionen $f(x) = x^2 - 2x + 2$ und $g(x) = 2x + 2$ ?

Lösung Aufgabe 2
Zunächst müssen die Schnittpunkte der Funktionen bestimmt werden:

$f(x) = g(x)$

$\begin{array}{rcll} f(x) & = & g(x) &\\ x^2 - 2x + 2 & = & 2x + 2 & \vert -2x\ \vert -2 \\ x^2 - 2x -2x & = & 2 - 2 & \\ x^2 - 4x & = & 0 & \\ x \cdot (x - 4) & = & 0 &\\ \end{array}$

Die Schnittpunkte liegen bei $x_1 = 0$ und $x_2 = 4$ . Nun können wir das Integral aufstellen. Die Schnittpunkte bilden die Integrationsgrenzen.

$\displaystyle \int \limits_{0}^{4} \left[g(x) - f(x) \right] ~\text{d}x$
$\quad \displaystyle = \int \limits_{0}^{4} \left[(2x + 2) - (x^2 - 2x + 2) \right] ~\text{d}x$
$\quad \displaystyle = \int \limits_{0}^{4} \left[2x + 2 - x^2 + 2x - 2 \right] ~\text{d}x$
$\quad \displaystyle = \int \limits_{0}^{4} \left[-x^2 + 4x \right] ~\text{d}x$

Im Anschluss können wir das Integral lösen:
$\displaystyle \int \limits_{0}^{4} \left[-x^2 + 4x \right] ~\text{d}x$

$\quad = \left[ -\dfrac{1}{3}x^3 + \dfrac{1}{2} \cdot 4x^2 \right]_0^4$

$\quad = \left( - \dfrac{1}{3} \cdot 4^3 + \dfrac{1}{2} \cdot 4 \cdot 4^2\right) - \left( -\dfrac{1}{3} \cdot 0^3 + \dfrac{1}{2} \cdot 4 \cdot 0^2\right)$

$\quad = \left(- \dfrac{64}{3} + 32\right) - 0 = \dfrac{32}{3}$

Die Fläche zwischen den Graphen der Funktionen $f(x)$ und $g(x)$ hat eine Größe von $\frac{32}{3}~\text{FE}$ .

Häufig gestellte Fragen zum Thema Integral

Was ist Integralrechnung?

Die Integralrechnung umfasst das Rechnen mit Integralen. Diese dienen dazu, Flächeninhalte zwischen dem Graphen einer Funktion und der $x$ -Achse oder den Flächeninhalt zwischen zwei Graphen zu berechnen.

Wie berechnet man Integrale?

Um Integrale zu berechnen, wird zunächst eine Stammfunktion $F(x)$ gebildet. Dazu wird die Funktion $f(x)$ integriert. Dabei gilt:
$F^\prime (x) = f(x)$

Was ist das unbestimmte Integral?

Das unbestimmte Integral umfasst alle Stammfunktionen einer Funktion:
$\displaystyle \int f(x) ~\text{d}x = F(x) + c$ mit $c \in \mathbb{R}$

Was gibt das bestimmte Integral an?

Sind Integrationsgrenzen vorgegeben, wird aus dem unbestimmten ein bestimmtes Integral. Dieses lässt sich mit dem Hauptsatz der Integralrechnung lösen:
$\displaystyle \int \limits_{a}^{b} f(x) ~\text{d}x = \Bigl[ F(x) \Bigr]_a^b = F(b) - F(a)$

Was ist das Integral von 0?

$0$ integriert ergibt $0 \cdot x = 0$ .

Welches bestimmte Integral hat den Wert 0?

Schließt ein Funktionsgraph in einem Intervall Flächen oberhalb und unterhalb der $x$ -Achse ein, können diese sich ausgleichen. Sind beide Flächen exakt gleich groß, ist der Wert des bestimmten Integrals gleich 0.

Integral und Integralrechnung – Erklärung

Inhaltsverzeichnis zum Thema Integral

Das Integral im Überblick

Leave A Comment Antworten abbrechen