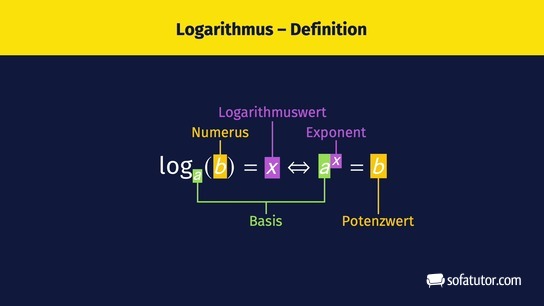
Der Logarithmus – Definition und Eigenschaften

Erfahre, wie der Logarithmus Potenzieren umkehrt und den Exponenten bestimmt. Entdecke die Definition, Regeln und besondere Logarithmen wie den natürlichen Logarithmus und Logarithmus zu verschiedenen Basen. Dies und vieles mehr findest du im folgenden Text!

Inhaltsverzeichnis zum Thema Logarithmus

Der Logarithmus einfach erklärt
Logarithmus – Definition und Regeln
Logarithmus – Definition
Logarithmus – Beispiel
Logarithmus – Rechenregeln und Logarithmusgesetze mit Herleitung
Besondere Logarithmen
Der natürliche Logarithmus
Der Logarithmus zur Basis $10$
Logarithmus- und Exponentialfunktionen
Häufig gestellte Fragen zum Thema Logarithmus

Der Logarithmus im Überblick

Der Logarithmus kehrt das Potenzieren um. Anders als das Wurzelziehen liefert der Logarithmus den Exponent einer Potenz bei gegebener Basis:
$log_{a}{b} = x \quad \Leftrightarrow \quad a^x = b$
Der Logarithmus erfüllt die Rechenregeln $\log_a(y\cdot z) = \log_a(y) + \log_a(z)$ und $\log_a(y^z) = z \cdot \log_a(y)$ .
Die Basis des Logarithmus $\log_a$ ist immer eine positive reelle Zahl $a \neq 1$ . In den Logarithmus kannst du keine negativen Zahlen einsetzen.
Der natürliche Logarithmus $\ln$ ist der Logarithmus zur Basis $e$ (eulersche Zahl), also $\ln=\log_e$ .

Quelle sofatutor.com

❮ ❯

Was heißt Logarithmus?

Der Logarithmus einfach erklärt

Ähnlich wie das Wurzelziehen ist auch das Anwenden des Logarithmus eine Umkehrung des Potenzierens.

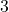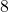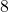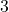Beim Wurzelziehen sind Potenzwert und Exponent gegeben und die Basis ist gesucht: Wenn wir $\sqrt[3]{8}$ berechnen, lösen wir die Gleichung $x^3=8$ . Wir bestimmen also die passende Basis zum Exponenten $3$ und dem Potenzwert $8$ . Mit anderen Worten: Wir beantworten die Frage: Bei welcher Basis $x$ kommt der Potenzwert $8$ heraus, wenn ich $x$ mit dem Exponenten $3$ potenziere? Die gesuchte Basis $x$ heißt die dritte Wurzel von $8$ . 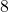Wir schreiben: $x=\sqrt[3]{8}$ .
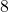Beim Anwenden des Logarithmus sind Potenzwert und Basis gegeben und der passende Exponent ist gesucht: Wir wollen die Gleichung $2^x=8$ nach $x$ auflösen, d. h., wir suchen zum Potenzwert $8$ und zur Basis 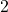$2$ den passenden Exponenten. Mit anderen Worten: Wir beantworten die Frage: Mit welchem Exponenten muss ich die Basis 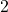$2$ potenzieren, um den Potenzwert 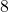$8$ zu erhalten? 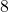Der gesuchte Exponent $x$ heißt der Logarithmus von $8$ zur Basis 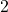$2$ . Wir schreiben: $x=\log_2(8)$ . 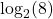Um den Logarithmus $\log_2(8)$ zu bestimmen, betrachten wir die Potenzen zur Basis 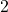$2$ . 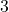Wir finden $2^3=8$ , daher ist $3$ der gesuchte Exponent $x$ , also $\log_2(8)=3$ .

Logarithmus – Definition und Regeln

Jeder Logarithmus gehört zu einer festgelegten Basis. Wir betrachten zuerst die Basis $2$ . Der Logarithmus (zur Basis $2$ ) einer natürlichen Zahl $y$ ist diejenige Zahl $x$ , für die gilt:
$2^x = y$
Man schreibt: $x=\log_2(y)$ .
Die Zahl $x$ ist durch die Basis und den Potenzwert $y$ eindeutig festgelegt. Ändern wir die Basis oder den Potenzwert, ändert sich auch der Wert des Logarithmus.

Logarithmus – Definition

Was wir eben für die Basis $2$ erklärt haben, können wir ganz analog für jede beliebige positive Zahl als Basis machen. Wir erhalten so die allgemeine Definition des Logarithmus: Sind $a$ und $b$ positive reelle Zahlen und ist $a\neq 1$ , heißt eine reelle Zahl $x$ der Logarithmus von $b$ zur Basis $a$ , falls gilt: $a^x=b$ . Wir schreiben also:

$x=\log_a(b) \quad \Leftrightarrow \quad a^x=b$

In Worten: Die Basis $a$ der Potenz schreiben wir bei dem Logarithmus als Index. Der Potenzwert $b$ ist der Numerus des Logarithmus (man sagt auch: das Argument des Logarithmus). Der Logarithmus schließlich ist der gesuchte Exponent $x$ .

Die Basis des Logarithmus muss eine positive Zahl sein. Denn für eine negative Zahl $a$ als Basis ist die Gleichung $a^x=b$ im Allgemeinen nicht lösbar. Zum Beispiel ist für $a=-2$ die Gleichung $(-2)^x=8$ nicht lösbar. Denn es gibt keine Zahl, mit der $-2$ potenziert den Wert $8$ annimmt. Die Basis $a$ darf auch nicht $0$ sein. Denn die Gleichung $0^x=b$ ist nur dann lösbar, wenn $b =0$ ist. Aber selbst in diesem Fall ist die Gleichung nicht eindeutig lösbar, d. h., es ist kein eindeutiger Wert $x$ bestimmbar.

Die Basis des Logarithmus darf auch nicht $1$ sein, denn jede Potenz von $1$ ist $1$ . Daher ist die Gleichung $1^x=b$ nicht lösbar, wenn $b \neq 1$ ist.

Der Numerus des Logarithmus darf keine negative Zahl sein, denn jede Potenz einer positiven Basis $a$ ist wieder eine positive Zahl $b$ . Mit anderen Worten: Für negative Potenzwerte ist die Gleichung $a^x=b$ nicht lösbar, da die Basis $a$ immer positiv ist.

Der Numerus des Logarithmus darf auch nicht $0$ sein, denn Potenzen einer positiven Basis sind immer positiv und ergeben niemals den Potenzwert $0$ . Mit anderen Worten: Die Gleichung $a^x=0$ mit $a > 0$ ist nicht lösbar.

Der Logarithmus jeder beliebigen Basis $a$ nimmt aber den Wert $0$ an: Für jede Basis $a$ ist $\log_a(1) =0$ , denn für jede positive Zahl $a$ ist $a^0=1$ . Diese Gleichung ist eine Folgerung des Potenzgesetzes.

Der Logarithmus jeder Basis $a$ nimmt auch den Wert $1$ an: Für jede Basis $a$ ist $\log_a(a) =1$ . Denn für jede positive Zahl $a$ ist $a^1=a$ .

Die beiden äquivalenten Gleichungen $a^x=b$ und $\log_a(b)=x$ aus der Definition des Logarithmus können wir auch ineinander einsetzen:

Setzen wir den Logarithmus $x=\log_a(b)$ als Exponenten der Potenz $a^x$ ein, erhalten wir den Numerus des Logarithmus:
$a^{\log_a(b)} = b$
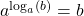
Setzen wir umgekehrt die Potenz $a^x$ in den Logarithmus zur Basis $a$ ein, erhalten wir wieder den Exponenten, also den Numerus der Exponentialfunktion zur Basis $a$ :
$\log_a(a^x) = x$

Logarithmus – Beispiel

Wir wollen die Gleichung $3^x=81$ nach $x$ auflösen. Da der gesuchte Wert $x$ im Exponenten steht, ist das Auflösen nach $x$ eine Anwendung des Logarithmus. Wir müssen den Logarithmus zur Basis $3$ (also $\log_3$ ) verwenden, denn in der Potenzgleichung $3^x=81$ ist die Basis $3$ . In $\log_3$ setzen wir den Potenzwert $81$ ein. Mit dem Taschenrechner erhalten wir:
$\log_3(81) = 4$
Wenn wir keinen Taschenrechner zur Hand haben, können wir versuchen, den richtigen Logarithmus selbst zu berechnen. Dazu bestimmen wir beispielsweise die Potenzen zur Basis $3$ , bis wir den gewünschten Wert erhalten:
$\begin{array}{lcr} 3^2 &=& 9 \\ 3^3 &=& 27 \\ 3^4 &=& 81 \end{array}$
Die letzte Gleichung zeigt:
$\log_3(81) = 4$

Logarithmus – Rechenregeln und Logarithmusgesetze mit Herleitung

Die wichtigsten Rechenregeln für den Logarithmus sind Umkehrungen von Potenzgesetzen.

Wir beginnen mit dem Potenzgesetz der Addition von Exponenten. Für eine positive Basis $a$ und beliebige Exponenten $m$ und $n$ gilt das Potenzgesetz:
$a^{m+n} = a^m \cdot a^n$

Wir bezeichnen die beiden Potenzwerte auf der rechten Seite als $y=a^m$ und $z=a^n$ . Jetzt können wir die Gleichung
$a^{m+n} = y \cdot z = a^m \cdot a^n$
nach dem Exponenten links auflösen und erhalten:
$m+n = \log_a(y \cdot z)$
Da $y=a^m$ und $z=a^n$ gilt, ist $m=\log_a(y)$ und $n=\log_a(z)$ . Setzen wir diese Darstellung oben ein, erhalten wir die Formel:
$\log_a(y) + \log_a(z) = \log_a(y\cdot z)$
Diese Formel wird als Gesetz der Addition von Logarithmen bezeichnet.

Das Potenzgesetz der Multiplikation von Exponenten lautet:
$a^{m \cdot n} = (a^m)^n$
Setzen wir $a^m=z$ , haben wir:
$\log_a(z^n) = \log_a((a^m)^n) = \log_a(a^{m\cdot n}) = m \cdot n = n \cdot \log_a(z)$
Die Formel
$\log_a(z^n) = n \cdot \log_a(z)$
wird als Gesetz der Multiplikation von Logarithmen oder Regel des Logarithmus von Potenzen bezeichnet.

Ein weiteres Logarithmusgesetz beschreibt die Umwandlung von Logarithmen zu verschiedenen Basen ineinander.
Wir definieren $x=\log_b(y)$ und können damit $\log_a(y)$ wie folgt berechnen:

Wir schreiben zuerst $y=b^x$ . Darauf wenden wir den Logarithmus zur Basis $a$ an und verwenden die Regel für den Logarithmus von Potenzen:
$\log_a(y) = \log_a(b^x) = x \cdot \log_a(b)$
Nun setzen wir 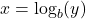$x=\log_b(y)$ ein und erhalten die Formel:
$\log_a(y) = \log_b(y) \cdot \log_a(b)$
Zuletzt bringen wir beide Terme des Logarithmus zur Basis $a$ auf eine Seite der Gleichung, erhalten wir (sofern 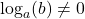$\log_a(b) \neq 0$ ):
$\log_b(y) = \dfrac{\log_a(y)}{\log_a(b)}$

Mit dieser Formel können wir jeden Logarithmus zur Basis $a$ in den entsprechenden Logarithmus zur Basis $b$ umrechnen (und umgekehrt).

Beachte: Der Bruch auf der rechten Seite ist nicht definiert, wenn der Nenner $0$ ist. Aber $\log_a(b)$ ist genau dann $0$ , wenn $b=1$ ist. Aber $b=1$ hatten wir als Basis eines Logarithmus ausgeschlossen. Daher gilt die Umrechnungsformel für alle Logarithmen.

In der folgenden Tabelle siehst du noch einmal die Logarithmusgesetze auf einen Blick:

Logarithmus von …	Rechenregel/Formel
Produkt	$\log_a(y \cdot z) = \log_a(y) + \log_a(z)$
allgemeiner Potenz	$\log_a(y^z) = z \cdot \log_a(y)$
spezieller Potenz	$\log_a(a^x) = x$
$1$	$\log_a(1) =0$
negativer Zahl	nicht definiert
$0$	nicht definiert
anderer Basis	$\log_b(y) = \dfrac{\log_a(y)}{\log_a(b)}$

Besondere Logarithmen

Für Logarithmen, die besonders häufig verwendet werden, gibt es abkürzende Schreibweisen, die das Rechnen mit Logarithmen übersichtlicher machen.

Der natürliche Logarithmus

Beim Rechnen mit Logarithmen gibt es eine spezielle Basis, nämlich die eulersche Zahl $e$ . Der Logarithmus zur Basis $e$ wird auch als natürlicher Logarithmus bezeichnet. Wir schreiben $\ln$ (lat.: logarithmus naturalis) anstelle von $\log_e$ .

Du kannst den Logarithmus zu einer beliebigen Basis $a$ mithilfe des natürlichen Logarithmus berechnen. Die Formel dazu ist genau die Umrechnungsformel aus dem vorigen Abschnitt. Mit der Schreibweise $\ln$ anstelle von $\log_e$ ist sie leichter zu merken:

Für jeden Logarithmus zur Basis $a$ und jede positive Zahl $y$ gilt:
$\log_a(y) = \dfrac{\ln(y)}{\ln(a)}$

Der Logarithmus zur Basis $10$

Eine spezielle Rolle spielt auch der Logarithmus zur Basis $10$ . Statt $\log_{10}$ sind auch die Bezeichnungen $\log$ (ohne Index) oder $\lg$ gebräuchlich. Den Logarithmus zur Basis $10$ kannst du einfach verstehen, wenn der Numerus eine Zehnerpotenz ist: Der Exponent einer Zehnerpotenz ist das Gleiche wie die Anzahl der Nullen ihres Potenzwerts. Es ist nämlich $10^1 =10$ (eine Eins mit einer Null), $10^2 = 100$ (eine Eins mit zwei Nullen), $10^5 = 100\,000$ (eine Eins mit fünf Nullen) und so weiter. Den Logarithmus zu berechnen, bedeutet, den Exponenten zu bestimmen. Es ist also $\log(10^5) = 5$ . Ganz allgemein gilt für beliebige positive Exponenten:
$\log(10^n) = n$

Logarithmus- und Exponentialfunktionen

Der Logarithmus ist eine Umkehrung des Potenzierens, bei der die Basis gegeben ist. Wir wählen eine beliebige Basis $a > 0$ mit $a\neq 1$ und betrachten Potenzen und Logarithmen zur Basis $a$ . Den Zusammenhang zwischen Potenzen und Logarithmen beschreiben wir durch die Äquivalenz:
$x=\og_a(y) \quad \Leftrightarrow \quad a^x=y$
Die Variablen $x$ und $y$ in diesen beiden Gleichungen verraten schon, dass wir diese Gleichungen im Koordinatensystem darstellen können. Setzen wir in die Potenz $a^x$ verschiedene Werte für $x$ ein, erhalten wir die Exponentialfunktion zu Basis $a$ .

Vertauschen wir nun die Rollen von $x$ und $y$ und lesen die Gleichung $a^x=y$ oder die äquivalente Gleichung $x=\log_a(y)$ als Funktion mit der unabhängigen Variablen $y$ und der abhängigen Variablen $x$ , erhalten wir die Logarithmusfunktion zur Basis $a$ .

Ganz analog erhalten wir den Funktionsgraphen der Logarithmusfunktion zur Basis $a$ aus dem Funktionsgraphen der Exponentialfunktion zur Basis $a$ , indem wir die $x$ -Achse und die $y$ -Achse tauschen. Das Tauschen der Koordinatenachsen entspricht einer Spiegelung der Funktionsgraphen an der Diagonale des ersten und dritten Quadranten oder – anders gesagt – einer Spiegelung am Funktionsgraphen der Funktion $h(x)=x$ .

Im Bild siehst du die Funktionsgraphen der Exponentialfunktion zur Basis $2$ , also $g(x) = 2^x$ , und der zugehörigen Logarithmusfunktion zur Basis $2$ , also $f(x) = \log_2(x)$ .

Logarithmusfunktion und Experimentalfunktion

Wählen wir speziell die eulersche Zahl $e$ als Basis, erhalten wir die Exponentialfunktion zur Basis $e$ und den natürlichen Logarithmus:
$x=\ln(y) \quad \Leftrightarrow \quad e^x=y$

Der Zusammenhang der Exponentialfunktion (oder $e$ -Funktion) mit der Logarithmusfunktion wird durch den Begriff der Umkehrfunktion ausgedrückt: Die Logarithmusfunktion ist die Umkehrfunktion der Exponentialfunktion und die Exponentialfunktion ist die Umkehrfunktion der Logarithmusfunktion.
Wir schreiben auch:

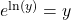$e^{\ln(y)} = y$ und
$\ln(e^x)=x$ .

Mit anderen Worten: Steht der natürliche Logarithmus im Exponenten der $e$ -Funktion, erhält man den Numerus des Logarithmus. Steht eine $e$ -Funktion im Numerus des natürlichen Logarithmus, erhält man den Numerus des Logarithmus.

Häufig gestellte Fragen zum Thema Logarithmus

Was ist ein Logarithmus?

Der Logarithmus einer Zahl $y$ zur Basis $a$ ist diejenige Zahl, mit der du $a$ potenzieren muss, um den Potenzwert $y$ zu erhalten. Der Logarithmus von $8$ zur Basis $2$ ist $3$ , denn $2^3=8$ . Wir schreiben: $\log_2(8)=3$ . Der Logarithmus von $10\,000$ zur Basis $10$ ist $4$ , denn die Zahl $10\,000$ hat vier Nullen: $10\,000 = 10^4$ , daher ist $\log_{10}(10\,000) = 4$ .

Was sagt mir der Logarithmus?

Der Logarithmus $\log_a(y)$ besagt, welchen Exponenten du nehmen musst, um durch Potenzieren einer gegebenen Basis $a$ einen gewünschte Potenzwert $y$ zu erhalten. Mit anderen Worten: $x = \log_a(y)$ bedeutet, dass $a^x=y$ ist. Beispielsweise ist der Logarithmus $\log_2(8)$ derjenige Exponent, mit dem man die Basis $2$ potenzieren muss, um den Potenzwert $8$ zu erhalten. Es gilt: $\log_2(8) = 3$ , denn $2^3=8$ .

Warum braucht man den Logarithmus?

Du brauchst den Logarithmus zur Basis $a$ , um eine Potenzgleichung $a^x =y$ nach $x$ aufzulösen. Der Logarithmus kehrt also (ähnlich wie das Wurzelziehen) das Potenzieren um.

Was macht der Logarithmus?

Der Logarithmus zur Basis $a$ bestimmt denjenigen Exponenten, den du brauchst, um durch Potenzieren der Basis $a$ einen vorgegebenen Potenzwert $y$ zu erhalten. Der Logarithmus von $8$ zur Basis $2$ ist $3$ , denn $2^3=8$ . Wir schreiben daher: $\log_2(8) =3$

Was berechnet man mit dem Logarithmus?

Mit dem Logarithmus zur Basis $a$ berechnest du den passenden Exponenten, um beim Potenzieren von $a$ einen gewünschten Potenzwert $y$ zu erhalten. Ist $2^x=8$ , ist $x$ der Exponent, mit dem man $2$ potenzieren muss, um $8$ zu erhalten. Die gesuchte Zahl $x$ ist der Logarithmus von $8$ zur Basis $2$ , also $x=\log_2(8)$ .

Wie löse ich den Logarithmus auf?

Den Logarithmus bestimmst du, indem du eine Potenzgleichung nach dem Exponenten auflöst: Bei der Gleichung $2^x=8$ setzt du den Potenzwert $8$ in den Logarithmus $\log_2$ zur Basis $2$ ein und erhältst $\log_2(8)=3$ .

Wie rechne ich mit dem Logarithmus?

Die wichtigsten Rechengesetze für den Logarithmus sind:

$\log_a(y \cdot z) = \log_a(y) + \log_a(z)$
$\log_a(y^z) = z \cdot \log_a(y)$
$\log_b(y) = \frac{\log_a(y)}{\log_a(b)}$ und $\log_b(y) = \dfrac{\ln(y)}{\ln(b)}$
$\log_a(1) =0$
$\log_a(a^x) = x$ und $a^{\log_a(y)}=y$

Hierbei sind $a$ und $b$ beliebige Basen für den Logarithmus, d. h., $a$ und $b$ sind beide positiv und beide nicht $1$ .

Wie rechnet man Logarithmus ohne Taschenrechner?

Um den Logarithmus einer Zahl zu berechnen, betrachtest du die Potenzen der Basis. Das geht auch ohne Taschenrechner. Nehmen wir als Beispiel den Logarithmus zur Basis $2$ . Wir schreiben die Zweierpotenzen auf: $2^1=2$ , daher ist $\log_2(2)=1$ . Die nächste Potenz von $2$ ist $2^2=4$ . Also ist $\log_2(4) = 4$ . Und $2^3=8$ , also $\log_2(8)=3$ .

Wann braucht man den natürlichen Logarithmus?

Mit dem natürlichen Logarithmus kehrst du Potenzen zur Basis $e$ um. Hierbei steht $e$ für die eulersche Zahl. Die Gleichung $e^x=y$ ist äquivalent zu $\ln(y) =x$ .

Wann benutze ich welchen Logarithmus?

Der Logarithmus muss immer zur Basis passen, die du bei den Potenzrechnungen verwendest. Rechnest du mit Potenzen von $2$ , verwendest du $\log_2$ , bei Zehnerpotenzen aber $\log_{10}$ . Rechnest du mit Potenzen der eulerschen Zahl $e$ , verwendest du den natürlichen Logarithmus $\ln=\log_e$ .

Wie berechnet man log10?

Den Logarithmus zur Basis $10$ kannst du mit dem Taschenrechner berechnen. Du kannst auch direkt mit Zehnerpotenzen rechnen. Der Logarithmus (zur Basis $10$ ) von einer vorgegebenen Zehnerpotenz ist der Exponent dieser Zehnerpotenz. Das ist das Gleiche wie die Anzahl der Nullen der Zehnerpotenz: $10^4 = 10\,000$ und $\log_{10}(10,\,000) = 4$ .

Was ist der Unterschied zwischen ln und log?

Mit dem Symbol $\ln$ bezeichnet man den Logarithmus zur Basis $e$ , also: $\ln = \log_{e}$ . Hierbei ist $e$ die eulersche Zahl. Der Logarithmus zur Basis $e$ heißt auch natürlicher Logarithmus. Die Abkürzung $\ln$ steht für logarithmus naturalis (lat: natürlicher Logarithmus). Die Bezeichnung $\log$ (ohne Index) wird entweder für den natürlichen Logarithmus oder für den Logarithmus zur Basis $10$ verwendet.

Wie lauten die wichtigsten Rechenregeln für log?

Die wichtigsten Rechenregeln für den Logarithmus zu beliebigen Basen $a$ und $b$ sind:

$\log_a(y \cdot z) = \log_a(y) + \log_a(z)$
$\log_a(y^z) = z \cdot \log_a(y)$
$\log_b(y) = \frac{\log_a(y)}{\log_a(b)}$ und analog $\log_b(y) = \dfrac{\ln(y)}{\ln(b)}$
$\log_a(1) =0$
$\log_a(a^x) = x$ und $a^{\log_a(y)}=y$

Wann wird der Logarithmus angewendet?

Den Logarithmus wendest du an, wenn du das Potenzieren rückgängig machen willst und dabei der Exponent gesucht ist. Es unterscheidet sich vom Wurzelziehen. Beim Wurzelziehen machst du das Potenzieren rückgängig und suchst die Basis.

Warum ist der Logarithmus einer negativen Zahl nicht definiert?

Beim Potenzieren einer positiven Basis $b$ ist das Ergebnis immer positiv. Es gibt keinen Exponenten $x$ , für den $b^x$ negativ ist, daher gibt es keinen Logarithmus einer negativen Zahl.

Warum kann der Logarithmus nicht negativ sein?

Der Wert des Logarithmus kann negativ sein. Beispielsweise ist $\log_2(0,25) = -2$ . Aber du kannst keine negative Zahl in den Logarithmus einsetzen. Denn Potenzen einer positiven Zahl können nicht negativ werden.

Der Logarithmus – Definition und Eigenschaften

Inhaltsverzeichnis zum Thema Logarithmus

Der Logarithmus im Überblick

Leave A Comment Antworten abbrechen