Terme und Gleichungen in Mathe – Definition, Erklärung und Beispiele
Terme kombinieren Zahlen und Variablen durch Rechenzeichen, während Gleichungen zwei Terme mit einem Gleichheitszeichen verknüpfen. Lerne, wie man Gleichungen löst und welche Arten es gibt. Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Terme und Gleichungen
Terme und Gleichungen – Definitionen
Terme und (Un-)Gleichungen werden dir sowohl im Alltag als auch in der Schule immer wieder begegnen, z. B. beim Berechnen des Umfangs eines Vielecks oder beim Umstellen einer Formel in Mathe oder Physik oder anderen naturwissenschaftlichen Fächern.
Ein Term kann eine Kombination lediglich aus Zahlen (z. B. ![]() ) sein oder auch Variablen und Klammern enthalten (z. B.
) sein oder auch Variablen und Klammern enthalten (z. B. ![]() ). Diese werden sinnvoll durch ein Rechenzeichen wie
). Diese werden sinnvoll durch ein Rechenzeichen wie ![]() verbunden.
verbunden.
Auch eine einzelne Zahl (mit Vorzeichen) ist ein Term (z. B. ![]() oder
oder ![]() ).
).
Eine Gleichung verknüpft zwei solche Terme mit einem Gleichheitszeichen ![]() . Dies besagt, dass der Term auf der linken Seite den gleichen Wert hat wie der Term auf der rechten Seite des Gleichheitszeichens (z. B.
. Dies besagt, dass der Term auf der linken Seite den gleichen Wert hat wie der Term auf der rechten Seite des Gleichheitszeichens (z. B. ![]() ).
).
Eine Ungleichung verknüpft zwei Terme statt mit einem ![]() durch ein Vergleichszeichen wie kleiner als (
durch ein Vergleichszeichen wie kleiner als (![]() ), größer als (
), größer als (![]() ), kleiner oder gleich (
), kleiner oder gleich (![]() ) oder größer oder gleich (
) oder größer oder gleich (![]() ): z. B.
): z. B. ![]() .
.
Aufstellen von Termen und Gleichungen
Nach der Erklärung von Termen und Gleichungen wollen wir uns nun das Aufstellen von Termen bzw. Gleichungen anschauen. Dies machen wir am einfachsten an einer kleinen Textaufgabe:
Du möchtest mit zwei Freunden mit dem Bus in die Stadt fahren. Der Fahrer nennt euch einen Gesamtpreis von ![]() . Wie viel muss jeder von euch zahlen?
. Wie viel muss jeder von euch zahlen?
Wir haben also gegeben: ![]() Fahrer (du und zwei Freunde) kosten insgesamt
Fahrer (du und zwei Freunde) kosten insgesamt ![]() .
.
Die Variable ![]() steht im Folgenden für den gesuchten Betrag, den jeder Einzelne von euch zahlen muss. Beim Aufstellen der Terme und Gleichung lassen wir die Einheit
steht im Folgenden für den gesuchten Betrag, den jeder Einzelne von euch zahlen muss. Beim Aufstellen der Terme und Gleichung lassen wir die Einheit ![]() weg.
weg.
Die Kosten für drei Personen sind also:
![]()
Der zweite Term sind die Gesamtkosten:
![]()
Setzen wir die beiden Terme gleich, erhalten wir die Gleichung:
![]()
In Worten: Drei mal der gesuchte Betrag ![]() ergibt die bezahlten
ergibt die bezahlten ![]() . Das Gleichheitszeichen verknüpft also den linken Term
. Das Gleichheitszeichen verknüpft also den linken Term ![]() mit dem rechten Term
mit dem rechten Term ![]() .
.
Gleichungen umstellen und lösen
Um die Frage zu beantworten, müssen wir die Gleichung lösen, d. h. nach der Variable ![]() umstellen. Damit ist gemeint, dass die gesuchte Variable (hier
umstellen. Damit ist gemeint, dass die gesuchte Variable (hier ![]() ) allein auf einer Seite steht. Dabei darf die Aussage der Gleichung nicht verändert werden, weshalb dieses Verfahren auch „Äquivalenzumformung“ heißt, da die Gleichung von Schritt zu Schritt äquivalent, das bedeutet gleichwertig, bleibt. Dazu kannst du die vier Grundrechenarten Addition, Subtraktion, Multiplikation und Division verwenden. Wichtig ist hierbei, dass du darauf achtest, den jeweiligen Rechenschritt auf beiden Seiten der Gleichung durchzuführen.
) allein auf einer Seite steht. Dabei darf die Aussage der Gleichung nicht verändert werden, weshalb dieses Verfahren auch „Äquivalenzumformung“ heißt, da die Gleichung von Schritt zu Schritt äquivalent, das bedeutet gleichwertig, bleibt. Dazu kannst du die vier Grundrechenarten Addition, Subtraktion, Multiplikation und Division verwenden. Wichtig ist hierbei, dass du darauf achtest, den jeweiligen Rechenschritt auf beiden Seiten der Gleichung durchzuführen.
Beim Berechnen der Gleichung müssen wir also einige Regeln beachten:
- Rechenschritte müssen immer auf beiden Seiten durchgeführt werden.
- Die Punkt-vor-Strich-Regel muss beachtet werden, also zuerst die Multiplikation/Division und dann erst die Addition/Subtraktion durchführen.
- Durch
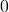 darf nicht geteilt werden.
darf nicht geteilt werden.
Für unser Beispiel bedeutet dies:
![Rendered by QuickLaTeX.com \begin{array}{ccccl} & 3 \cdot x & = & 12 & ~|~:3~~\text{(auf beiden Seiten durch 3 teilen)} \\[4pt] \Leftrightarrow & \frac{3\cdot x}{3} & = & \frac{12}{3} & ~|~\,~\text{(kürzen)}\\[4pt] \Leftrightarrow & x & = & 4 & \end{array}](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-127a59d057160afac34caa919813e614_l3.png)
Also bezahlt jeder von euch ![]() .
.
Arten von Gleichungen
Es gibt verschiedene Arten von Gleichungen, die verschiedene mathematische Ausdrücke enthalten können. Im Einführungsbeispiel haben wir die lineare Gleichung kennengelernt, die die Variable in der ersten Potenz enthält.
Je nach Art der Gleichung gibt es andere Lösungsansätze und Umformungen.
Bei all diesen Gleichungen kann das Gleichheitszeichen durch ein Vergleichszeichen (![]() ,
, ![]() ,
, ![]() ,
, ![]() ) ersetzt werden, wodurch man eine Ungleichung erhält.
) ersetzt werden, wodurch man eine Ungleichung erhält.
| Art der Gleichung | Erklärung | Beispiel |
|---|---|---|
| Lineare Gleichung | Variable in erster Potenz: |
|
| Quadratische Gleichung | Variable in zweiter Potenz |
|
| Potenzgleichung | Kann höhere Potenzen enthalten |
|
| Bruchgleichung | Variable steht im Nenner eines Bruchs |
Des Weiteren gibt es u. a. auch Exponentialgleichungen, logarithmische und trigonometrische Gleichungen, die du später noch kennenlernst.
Zusammenfassung – Terme und Gleichungen kurz und einfach erklärt
Terme bestehen aus Zahlen, Variablen und/oder Klammern, verknüpft durch Rechenzeichen. In Gleichungen werden zwei Terme durch ein Gleichheitszeichen verknüpft. Unsere Aufgabe ist es, die unbekannte Variable in der Gleichung durch Äquivalenzumformungen zu berechnen. Die Rechenschritte müssen immer auf beiden Seiten der Gleichung durchgeführt werden, bei einfachen linearen Gleichungen sind das Addition, Subtraktion, Multiplikation und Division (nicht durch ![]() teilen!). Des Weiteren muss die Punkt-vor-Strich-Regel beachtet werden.
teilen!). Des Weiteren muss die Punkt-vor-Strich-Regel beachtet werden.
Manchmal ist es hilfreich, zunächst die Terme zu vereinfachen, bevor man mit dem Lösen der Gleichung beginnt.
Beispiel:
![Rendered by QuickLaTeX.com \[\begin{array}{ccccl} & 2\cdot x + 4 \cdot x & = & 12 & ~| \quad \text{linken Term vereinfachen durch Ausklammern von $x$} \\\\[4pt] \Leftrightarrow & (2+4) \cdot x & = & 12 & \\\\[4pt] \Leftrightarrow & 6 \cdot x & = & 12 & ~| \quad :6 \quad \text{(auf beiden Seiten durch 6 teilen, sodass $x$ links allein steht)} \\\\[4pt] \Leftrightarrow & \dfrac{6 \cdot x}{6} & = & \dfrac{12}{6} & ~| \quad \text{kürzen} \\\\[4pt] \Leftrightarrow & x & = & 2 & \end{array}\] \end{document}](https://easy-schule.de/wp-content/ql-cache/quicklatex.com-f60d7d5cb51abc55f6883ad41975834b_l3.png)
Häufig gestellte Fragen zum Thema Terme und Gleichungen

