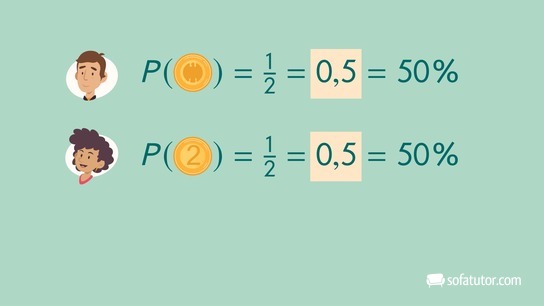Wahrscheinlichkeitsrechnung – Definitionen und Formeln

Erfahre, wie man Wahrscheinlichkeiten berechnet und welche Begriffe wichtig sind. Von Zufallsexperimenten bis hin zu Wahrscheinlichkeitsverteilungen – hier bekommst du einen Überblick.

Inhaltsverzeichnis zum Thema Wahrscheinlichkeitsrechnung

Wahrscheinlichkeitsrechnung im Überblick

  • Beim Rechnen mit Wahrscheinlichkeiten werden die Begriffe Ergebnis, Ereignis, Zufallsexperiment und Gegenwahrscheinlichkeit verwendet.

  • Bei mehrstufigen Zufallsexperimenten und bei der Berechnung der bedingten Wahrscheinlichkeit kann es helfen, ein Baumdiagramm aufzustellen.

  • Wahrscheinlichkeitsverteilungen stellen die Verteilung der Wahrscheinlichkeiten einer Zufallsvariable dar.

Wahrscheinlichkeitsrechnung: Lernvideo

Quelle: sofatutor.com

Was ist ein Zufallsversuch?
Was ist ein Zufallsversuch?
Was ist ein Zufallsversuch?Zufallsversuch mit einer MünzeP steht für Wahrscheinlichkeit (probability)unmöglich - möglich - sicherBeispiel mit einem Roulette Gewinne und NietenGewinne und Nieten - WahrscheinlichkeitZusammenfassung

Wahrscheinlichkeitsrechnung – Definition

Bei der Wahrscheinlichkeitsrechnung dreht sich alles um das Berechnen von Wahrscheinlichkeiten. Damit du mit Wahrscheinlichkeiten rechnen kannst, ist es wichtig, dass du einige Begriffe und Formeln kennst.

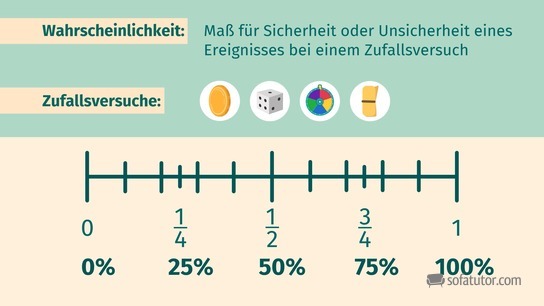
Meistens werden bei der Berechnung von Wahrscheinlichkeiten Zufallsexperimente betrachtet. Ein Zufallsexperiment kann verschiedene Ausgänge haben:

  • Jeder dieser Ausgänge ist ein sogenanntes Ergebnis.
  • Die Menge aller möglichen Ergebnisse ist die Ergebnismenge.
  • Ein Ereignis besteht aus einem oder mehreren Ergebnissen.
  • Ein Elementarereignis besteht aus einem einzigen Ergebnis.

Jedes Ereignis hat eine Wahrscheinlichkeit, die entweder als Dezimalzahl oder in Prozent angegeben sein kann. Wahrscheinlichkeiten liegen immer zwischen 0\,\% und 100\,\% bzw. zwischen 0 und 1.
Die Summe der Wahrscheinlichkeiten aller möglichen Ergebnisse eines Zufallsexperiments ist 1 bzw. 100\,\%

Die einfachsten Zufallsexperimente sind Laplace-Experimente, d. h. solche Experimente, bei der jedes Elementarereignis die gleiche Wahrscheinlichkeit hat.
Bei einem Laplace-Experiment kannst du die Wahrscheinlichkeit für ein Ereignis E mit folgender Formel berechnen:
P(E)=\dfrac{\text{Anzahl günstiger Ergebnisse}}{\text{Anzahl möglicher Ergebnisse}}

Häufig gewählte Beispiele für Zufallsexperimente sind:

  • der Würfelwurf,
  • das Drehen an einem Glücksrad und
  • das Ziehen von Losen.

Am Beispiel des Würfelwurfs ist das Würfeln der Augenzahl 6 ein Ereignis.
Die zugehörige Wahrscheinlichkeit ist P(6)=\dfrac{1}{6}, da eines von sechs Ergebnissen zum Ereignis gehört.

Es ist möglich, dass das gleiche Zufallsexperiment mehrmals hintereinander durchgeführt wird oder dass verschiedene Zufallsexperimente zusammengefasst werden. In beiden Fällen sprechen wir von einem mehrstufigen Zufallsexperiment.
Bei mehrstufigen Zufallsexperimenten kann es für das Berechnen von Wahrscheinlichkeiten helfen, wenn du ein Baumdiagramm erstellst.

Greifst du das vorherige Beispiel wieder auf, ist das folgende Baumdiagramm eine Möglichkeit, den zweimaligen Würfelwurf darzustellen.

Baumdiagramm Würfelwurf

Der Ausdruck \bar{6} steht für das Gegenereignis, also das Würfeln einer anderen Augenzahl als der 6. Die Wahrscheinlichkeit für ein Gegenereignis berechnet sich mit der Formel P(\bar{E})=1-P(E).

Am Beispiel des Würfelwurfs ist das P(\bar{6})=1-\dfrac{1}{6}=\frac{5}{6}.

Bedingte Wahrscheinlichkeit mithilfe des Baumdiagramms berechnen

Bedingte Wahrscheinlichkeiten lassen sich an einem Baumdiagramm direkt ablesen.
Die bedingte Wahrscheinlichkeit P(B \vert A) ist die Wahrscheinlichkeit dafür, dass das Ereignis B eintritt, unter der Voraussetzung, dass das Ereignis A bereits eingetreten ist.
In der folgenden Abbildung sind die bedingten Wahrscheinlichkeiten blau eingefärbt.

Baumdiagramm bedingte Wahrscheinlichkeit

Die bedingte Wahrscheinlichkeit ist definiert durch die Formel:
P(B \vert A)=\dfrac{P(A \cap B)}{P(A)}
Dabei ist P(A \cap B) die Wahrscheinlichkeit dafür, dass A und B gemeinsam eintreten (Schnittwahrscheinlichkeit). Sie entspricht auch dem Pfad aus den Ereignissen A und B.

Hast du eine Vierfeldertafel mit den einzelnen Wahrscheinlichkeiten gegeben oder berechnet, kannst du die bedingte Wahrscheinlichkeit mithilfe der Formel P(A\vert B = \frac{P(A\cap B)}{P(B)}) berechnen, ohne ein Baumdiagramm zu zeichnen. Die Wahrscheinlichkeit P(A \cap B) steht in einem der vier inneren Felder der Vierfeldertafel.

Laplace-Experiment – Erklärung und Beispiele

Ein Laplace-Experiment ist ein Zufallsexperiment, bei dem jedes Elementarereignis die gleiche Wahrscheinlichkeit besitzt.

Der Würfelwurf aus dem vorherigen Abschnitt ist beispielsweise ein Laplace-Experiment, da die Wahrscheinlichkeit für jede Augenzahl \frac{1}{6} ist.
Aber auch der Münzwurf kann als Beispiel für Laplace-Experimente betrachtet werden. Die beiden Ausgänge des Zufallsexperiments Kopf und Zahl besitzen die gleiche Wahrscheinlichkeit P(\text{Kopf})=P(\text{Zahl})= \frac{1}{2}.

Wahrscheinlichkeitsverteilungen

Eine Zufallsvariable X ist eine Größe, die von den Ergebnissen eines Zufallsexperiments abhängt. Für jeden Wert einer Zufallsvariable kann man die Wahrscheinlichkeit berechnen. Beispielsweise kann beim Würfeln mit zwei Würfeln die Summe der Augenzahlen jeden ganzzahligen Wert zwischen 2 (beide Würfeln zeigen 1) und 12 (beide Würfel zeigen 6 annehmen). Die Augensumme ist eine Zufallsvariable, denn der Wert der Augensumme hängt von den Ergebnissen des Würfelns ab. Für jeden möglichen Wert kann die Wahrscheinlichkeit, dass dieser Wert eintritt, berechnet werden.
Wahrscheinlichkeitsverteilungen sind Darstellungen, die die Verteilung der Gesamtwahrscheinlichkeit auf die Werte einer Zufallsvariablen angeben. Bei der Definition von Zufallsvariablen wird zwischen diskreten und stetigen Zufallsvariablen unterschieden.

  • Eine diskrete Zufallsvariable nimmt nur endlich viele Werte oder nur vereinzelt liegende Werte an.
  • Bei einer stetigen Zufallsvariable bilden die Werte ein Kontinuum.

Die wichtigsten Wahrscheinlichkeitsverteilungen lassen sich durch Kenngrößen charakterisieren.
Der Erwartungswert \mu oder E(X) einer Zufallsvariablen X gibt an, welcher Wert der Zufallsvariablen bei mehrmaliger Durchführung des Zufallsexperiments im Mittel zu erwarten ist.

Varianz und Standardabweichung sind Maße dafür, wie sehr die einzelnen Ergebnisse vom Erwartungswert abweichen. Man nennt sie auch Streumaße.
Die Varianz ist die mittlere quadratische Abweichung und wird berechnet durch Var(X) =\displaystyle\sum\limits_{i=1}^{n} (x_i - \mu)^{2} \cdot P(X = x_i).
Die Standardabweichung \sigma ist die Wurzel der Varianz, also \sigma=\sqrt{Var(X)}. Sie wird entsprechend auch als einfache quadratische Abweichung bezeichnet.

Binomialverteilung – Erklärung

Eine Binomialverteilung ist eine diskrete Wahrscheinlichkeitsverteilung, die auf einem Bernoulli-Experiment beruht. Bernoulli-Experimente sind definiert als Zufallsversuche mit nur zwei möglichen Ergebnissen. Das Ziehen von Losen mit den Möglichkeiten „Gewinn“ und „Niete“ ist zum Beispiel ein Bernoulli-Experiment.

Binomialverteilungen werden durch die Formel P(X=k)=\displaystyle \binom{n}{k} \cdot p^{k} \cdot (1-p)^{n-k} beschrieben. Dabei ist n die Anzahl der Durchgänge, k die Anzahl der Erfolge und p die Wahrscheinlichkeit für den Erfolg bei einer Durchführung. Die Formel gibt an, wie hoch die Wahrscheinlichkeit ist, bei n Durchführungen des Zufallsexperiments genau k Erfolge zu erzielen.

Du spielst ein Gesellschaftsspiel mit deinen Eltern und deinem Bruder. Insgesamt spielt ihr zehn Runden und die Wahrscheinlichkeit dafür, dass du gewinnst, liegt in jeder Runde bei 25\,\%. Es ist also

  • n=10
  • p=0,\!25

Um herauszufinden, wie wahrscheinlich es ist, dass du fünf der zehn Runden gewinnst, berechnest du P(5).

P(5)=\displaystyle \binom{10}{5} \cdot 0,\!25^{5} \cdot 0,\!75^{5}\approx0,058=5,\!84\,\%

Die Wahrscheinlichkeit dafür, dass du genau fünf der zehn Runden gewinnst, liegt also bei 5,84\,\%.

Poisson-Verteilung – Formel

Die Poisson-Verteilung gehört zu den diskreten Wahrscheinlichkeitsverteilungen. Sie wird beispielsweise verwendet, um die Binomialverteilung anzunähern.

Die Definition der Poisson-Verteilung lautet:
P(X=k)=\dfrac{\mu^{k}}{k!} \cdot e^{- \mu}

Poisson-Verteilungen werden häufig dazu verwendet, Zufallsexperimente zu beschreiben, bei denen das Vorkommen eines Ereignisses über einen bestimmten Zeitraum betrachtet wird.
Eine Besonderheit der Poisson-Verteilung ist, dass Erwartungswert und Varianz den gleichen Wert annehmen.

Normalverteilung – Erklärung

Die Normalverteilung wird auch als Gauß-Verteilung bezeichnet. Vielleicht hast du in diesem Zusammenhang schon etwas von der Glockenkurve gehört?  Der Funktionsgraph der Normalverteilung heißt auch Glockenkurve, weil er die Form einer Glocke hat.

Glockenkurve der Standardnormalverteilung

Die Normalverteilung gehört zu den stetigen Wahrscheinlichkeitsverteilungen, ist also auch für nicht ganzzahlige Werte r definiert.

Häufig gestellte Fragen zum Thema Wahrscheinlichkeitsrechnung

Bei der Wahrscheinlichkeitsrechnung dreht sich alles um das Rechnen mit Wahrscheinlichkeiten. Wichtige Begriffe der Wahrscheinlichkeitsrechnung sind Zufallsexperimente, Ergebnis und Ereignis, Zufallsvariablen und Verteilungen.

Zufallsexperimente sind Experimente, die drei Bedingungen erfüllen:

  • Die möglichen Ergebnisse sind bekannt.
  • Der Ausgang des Zufallsexperiments ist unvorhersehbar, d. h. zufällig.
  • Das Experiment ist unter identischen Bedingungen wiederholbar.

Bei einem Laplace-Experiment kann die Wahrscheinlichkeit für ein bestimmtes Ereignis E berechnet werden mit der Formel:
P(E)=\dfrac{\text{Anzahl der günstigen Ergebnisse}}{\text{Anzahl aller möglichen Ergebnisse}}

Die bedingte Wahrscheinlichkeit P(A\vert B) (auch P_B(A)) ist die Wahrscheinlichkeit dafür, dass ein Ereignis A eintritt, unter der Voraussetzung, dass ein Ereignis B bereits eingetreten ist.

Wahrscheinlichkeitsverteilungen sind Darstellungen, die zeigen, wie sich die Gesamtwahrscheinlichkeit auf die Werte einer Zufallsvariablen aufteilt.

In der Wahrscheinlichkeitsrechnung wird als Zufallsvariable eine Größe bezeichnet, die von den Ergebnissen eines Zufallsexperiments abhängt.

Die Normalverteilung gehört zu den stetigen Wahrscheinlichkeitsverteilungen. Sie hat die Form einer Glocke und wird deshalb auch als Glockenkurve bezeichnet.

Ein Bernoulli-Experiment ist ein Zufallsexperiment, das nur zwei mögliche Ausgänge hat. Beispielsweise ist das Werfen einer Münze ein Bernoulli-Experiment. Auch das blinde Raten in einem Test mit genau zwei möglichen Antworten ist ein Bernoulli-Experiment.

Die Binomialverteilung beruht auf einem Bernoulli-Experiment. Die Formel für die Binomialverteilung lautet \displaystyle P(X=k)=\binom{n}{k} \cdot p^{k} \cdot (1-p)^{n-k}.

Die Poisson-Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung. Sie wird häufig verwendet, wenn das Vorkommen eines Ereignisses über einen bestimmten Zeitraum betrachtet wird.

Jedes Baumdiagramm gehört zu einem mehrstufigen Zufallsexperiment. Ein Baumdiagramm erstellst du, indem du für jede Stufe des Zufallsexperiments alle möglichen Ereignisse mit den zugehörigen Wahrscheinlichkeiten aufzeichnest und die einzelnen Stufen durch Zweige und Pfade verbindest. Das wiederholst du so oft, wie das Zufallsexperiment Stufen hat.

Die Kombinatorik behandelt vor allem Abzähl- und Sortierprobleme, beispielsweise die Anzahl möglicher Anordnungen von Objekten oder Permutationen.

In der Wahrscheinlichkeitsrechnung wird Kombinatorik verwendet, um Wahrscheinlichkeiten von Ereignissen zu berechnen, die aus mehreren Ergebnissen kombiniert werden.

Als Ergebnis wird in der Wahrscheinlichkeitsrechnung jeder mögliche Ausgang eines Zufallsexperiments bezeichnet. Ein Ereignis besteht aus einem oder mehreren Ergebnissen. Beispielsweise besteht beim Würfeln das Ereignis, keine 4 zu würfeln, aus den Ergebnissen 1, 2, 3, 5 und 6.

Wenn du wissen möchtest, mit welcher Wahrscheinlichkeit du einen Gewinn bei einem Glücksspiel erzielst oder mit welcher Wahrscheinlichkeit du bei der nächsten Sitzordnung neben deinem besten Freund sitzt, kann dir die Wahrscheinlichkeitsrechnung in der Praxis nützlich werden.

Das einfachste Anwendungsgebiet der Wahrscheinlichkeitsrechnung sind Glücksspiele. Einige Beispiele sind:

  • Ziehen aus einem Lostopf
  • Drehen an einem Glücksrad
  • Werfen einer Münze

Formeln in der Wahrscheinlichkeitsrechnung hängen immer davon ab, was du berechnen möchtest. Zur Berechnung der Wahrscheinlichkeit eines einstufigen Zufallsexperiments verwendest du eine andere Formel als zur Berechnung der Wahrscheinlichkeit eines mehrstufigen Zufallsexperiments. Wieder eine andere Formel brauchst du zur Berechnung der bedingten Wahrscheinlichkeit und so weiter.

Leave A Comment

Alle Artikel aus dem Fach Mathematik