Prozentrechnung – Prozentsatz

Der Prozentsatz gibt das Verhältnis vom Prozentwert zum Grundwert an. Teilt man den Prozentwert durch den Grundwert , erhält man den Prozentsatz . Daher können wir den Prozentsatz mit der folgenden Formel berechnen:

Angegeben wird der Prozentsatz in Prozent (). Dabei steht Prozent für „durch Hundert“. Der Prozentsatz steht also für geteilt durch .

Hinweis: Den Prozentsatz können wir auch als Prozentzahl schreiben. Dafür wird in der Berechnung der Prozentwert noch mit multipliziert. Die Prozentzahl wird ohne Einheit, das heißt ohne Prozentzeichen, angegeben. Die Prozentzahl berechnen wir mit der Formel:

Begriffserklärung: Grundwert, Prozentwert und Prozentsatz
Bei dem Grundwert handelt es sich um den Wert, der entspricht. Er entspricht also der Gesamtzahl.
Der Prozentwert ist ein Teil des Grundwerts.
Der Prozentsatz gibt an, wie viel Prozent des Grundwerts dem Prozentwert entsprechen. Er gibt also den prozentualen Anteil an.

Angenommen wir haben Kugeln. dieser Kugeln sind grün. Das entspricht dann . Die Kugeln sind der Grundwert . Die grünen Kugeln sind der Prozentwert und die sind der Prozentsatz .

Die Grundlage der Berechnung des Prozentsatzes ist das Dreieck der Prozentrechnung.

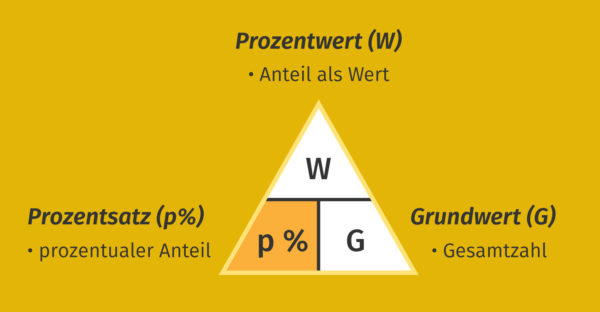
Dieses besagt, dass wir den Prozentsatz berechnen, indem wir den Prozentwert durch den Grundwert teilen.

Berechnen wir den Prozentsatz und die Prozentzahl nun an einem Beispiel.

Aufgabe
Wie viel Prozent sind von ? Berechne sowohl den Prozentsatz als auch die Prozentzahl.

Lösungsweg
Zunächst müssen wir aus der Aufgabe heraus den Prozentwert und den Grundwert bestimmen.

Um den Prozentsatz zu ermitteln, können wir die Werte nun in die entsprechende Formel einsetzen.

Um ein Ergebnis in Prozent anzugeben, ist es am leichtesten, wenn wir den Bruch so erweitern, dass im Nenner steht. In diesem Fall können wir den Bruch mit erweitern und erhalten:

Um die Prozentzahl zu ermitteln, setzen wir den Grundwert und den Prozentwert in die entsprechende Formel ein und erhalten:

Zur Berechnung des Prozentsatzes können wir auch den Dreisatz nutzen. Betrachten wir die Vorgehensweise an einem Beispiel: Wie viel Prozent sind von ?

Hier ist also der Prozentsatz zu Grundwert und Prozentwert gesucht.

Schritt 1: Zunächst setzen wir den Grundwert gleich . .

Schritt 2: Anschließend bestimmen wir den Prozentsatz zum Prozentwert . Dafür teilen wir den Grundwert und die durch .

Schritt 3: Um den gesuchten Prozentsatz zum Prozentwert zu ermitteln, multiplizieren wir nun beide Seiten mit .

(Prozentwert) entsprechen also (Prozentsatz) von (Grundwert).

Der Dreisatz kann auch in einer Tabelle dargestellt werden. Die folgende Tabelle zeigt, wie wir den Prozentsatz berechnen, wenn der Grundwert und der Prozentwert ist.

In der ersten Zeile wird der Grundwert gleich gesetzt. In der zweiten Zeile sind beide Werte durch geteilt, um den Prozentsatz zum Prozentwert zu ermitteln. In der dritten Zeile wurden beide Seiten mit multipliziert, um den gesuchten Prozentsatz zum Prozentwert zu errechnen.

Aufgaben zum Prozentsatz sind häufig Anwendungs- oder Sachaufgaben. Eine solche wollen wir nun betrachten.

Aufgabe
In einer Schulklasse sind Kinder. Von ihnen haben die Lieblingsfarbe Grün. Wie viel Prozent der Kinder in der Klasse haben Grün als Lieblingsfarbe?

Lösungsweg
Um den Prozentsatz auszurechnen, müssen wir zunächst den Grundwert und den Prozentwert bestimmen.

– Gesamtzahl der Kinder in der Klasse
– Teil der Kinder mit Lieblingsfarbe Grün

Nun können wir die beiden Werte in die Formel einsetzen.
Dabei können wir den Bruch mit kürzen und erhalten:

Diesen Bruch können wir mit erweitern, damit im Nenner steht, und so den Prozentsatz in Prozent angegeben:

Antwortsatz
Es haben der Kinder Grün als Lieblingsfarbe.

Hinweis: Auch wenn ein Prozentsatz größer als sein kann, kommt dies eher selten vor. Achte daher genau darauf, was gefragt ist und ob dein Ergebnis im Kontext der Aufgabe sinnvoll erscheint. Ein Beispiel: Wenn sich ein Preis von auf erhöht, dann entspricht der neue Preis des alten Preises. Oft ist aber nicht danach gefragt, auf welchen Prozentsatz (das wären die ), sondern um welchen Prozentsatz sich der Preis erhöht hat. In diesem Fall ist weiterhin , der Prozentwert ist hier allerdings die Differenz der Preise: , also die Preisänderung. Damit ergibt sich ein Prozentwert für die Preiserhöhung von .

Ist der Prozentwert größer als der Grundwert, dann ergibt sich ein Prozentsatz über . Die Vorgehensweise bleibt dabei unverändert. Betrachten wir dafür das folgende Beispiel:

Hinweis: Auch wenn ein Prozentsatz größer als sein kann, kommt dies eher selten vor. Achte daher genau darauf, was gefragt ist und ob dein Ergebnis im Kontext der Aufgabe sinnvoll erscheint. Ein Beispiel: Wenn sich ein Preis von auf erhöht, dann entspricht der neue Preis des alten Preises. Oft ist aber nicht danach gefragt, auf welchen Prozentsatz (das wären die ), sondern um welchen Prozentsatz sich der Preis erhöht hat. In diesem Fall ist weiterhin , der Prozentwert ist hier allerdings die Differenz der Preise: , also die Preisänderung. Damit ergibt sich ein Prozentwert für die Preiserhöhung von .