Primfaktorzerlegung – Erklärung und Beispiele
Natürliche Zahlen lassen sich als Produkt von Primzahlen darstellen, ein wichtiger Schritt bei der Bestimmung des größten gemeinsamen Teilers und kleinsten gemeinsamen Vielfachen. Lerne, wie die Primfaktorzerlegung funktioniert und wie sie in der Mathematik Anwendung findet. Dies und mehr im folgenden Text!
Inhaltsverzeichnis zum Thema Primfaktorzerlegung
Die Primfaktorzerlegung im Überblick
Quelle sofatutor.com
Primzahlen und Primfaktorzerlegung
Primzahlen sind Zahlen, die außer der 
und sich selbst keine weiteren Teiler haben. Die Zahl 
ist zum Beispiel eine Primzahl, da sie ohne Rest nur durch und teilbar ist. Im Gegensatz dazu ist die Zahl 
keine Primzahl, sie hat die ganzzahligen Teiler , 
, 
, und . Wir können die als Produkt aus Primzahlen schreiben: 
. Die Darstellung einer natürlichen Zahl als Produkt aus Primzahlen wird Primfaktorzerlegung genannt.
Es gilt: Für jede natürliche Zahl gibt es eine Primfaktorzerlegung, die bis auf die Reihenfolge der Faktoren eindeutig ist.
Ein Beweis für Existenz und Eindeutigkeit der Primfaktorzerlegung kann mittels Induktion geführt werden, wir verzichten an dieser Stelle auf eine Ausführung.
Primfaktorzerlegung bestimmen
Um die Primfaktorzerlegung einer Zahl zu berechnen, überprüfen wir diese nach und nach auf Teilbarkeit durch Primzahlen. Haben wir eine Primzahl gefunden, die Teiler der Zahl ist, führen wir die Division durch diesen sogenannten Primfaktor durch. Dann suchen wir nach weiteren Primfaktoren für das Ergebnis. Die Primfaktorzerlegung ist das Produkt aus allen Primfaktoren. Kommt der gleiche Primfaktor mehrfach in einer Zerlegung vor, wird er mit Potenzschreibweise abgekürzt:
Beispiel 1: Primfaktorzerlegung von 
ist nicht durch teilbar.
ist durch 
teilbar.
Wir rechnen:
ist durch teilbar.
Wir rechnen:
ist eine Primzahl.
Wir erhalten die Primfaktorzerlegung 
. Da der Primfaktor hier zweimal vorkommt, fassen wir 
als Potenz zu 
zusammen.
Es ist auch möglich, den Rechenweg bei der Primfaktorzerlegung in Form einer Tabelle darzustellen. Wir betrachten hierzu zwei Beispiele:
Beispiel 2: Primfaktorzerlegung von 
| 72 : 2 | 36 : 2 | 18 : 2 | 9 : 3 | 3 | |
|---|---|---|---|---|---|
| Primfaktor | |
|
|
|
|
Beispiel 2: Primfaktorzerlegung von 
| 130 : 2 | 65 : 5 | 13 | |
|---|---|---|---|
| Primfaktor | |
|
 |
Hinweis: Da es für die Primfaktorzerlegung keine Formel gibt, kann diese gerade bei großen Zahlen mit einem großen Aufwand verbunden sein. Diese Eigenschaft der Primfaktorzerlegung wird beispielsweise bei der Verschlüsselung von Daten genutzt, um diese vor unbefugtem Zugriff zu schützen.
Anwendungen der Primfaktorzerlegung
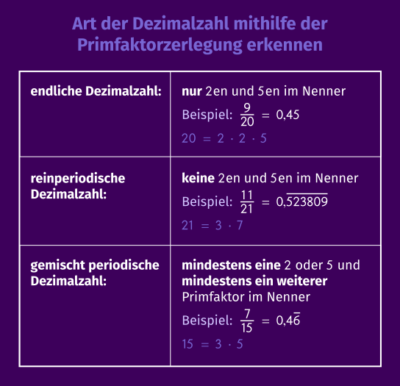
Die Zerlegung einer Zahl in Faktoren ist in vielen Bereichen in Mathe nützlich, beispielsweise wenn es darum geht, Brüche zu kürzen. An der Primfaktorzerlegung des Nenners eines vollständig gekürzten Bruchs können wir außerdem erkennen, wie der Bruch als Dezimalzahl geschrieben wird. Dabei können drei Fälle unterschieden werden:
- endliche Dezimalzahlen,
- reinperiodische Dezimalzahlen und
- gemischt periodische Dezimalzahlen.
Kriterien und Beispiele sind hier zusammengefasst:
Eine besondere Rolle spielt die Primfaktorzerlegung auch bei der Berechnung des größten gemeinsamen Teilers (kurz 
) und des kleinsten gemeinsamen Vielfachen (kurz 
), die wir nun kurz betrachten wollen.
Das kleinste gemeinsame Vielfache
Das kleinste gemeinsame Vielfache zweier Zahlen ist die kleinste Zahl, die ein ganzzahliges Vielfaches beider Zahlen ist.
Dabei gilt: Das kleinste gemeinsame Vielfache zweier Zahlen ist das Produkt aller Primfaktoren, die in einer der Primfaktorzerlegungen der Zahlen vorkommen.
Beispiel: 
Wir multiplizieren alle Primfaktoren, die in einer der beiden Zerlegungen vorkommen. Der gemeinsame Primfaktor taucht dabei nur einmal auf.
Der größte gemeinsame Teiler
Der größte gemeinsame Teiler zweier Zahlen ist die größte Zahl, die ein Teiler beider Zahlen ist.
Dabei gilt: Der größte gemeinsame Teiler zweier Zahlen ist das Produkt aller Primfaktoren, die gleichzeitig in den Primfaktorzerlegungen beider Zahlen vorkommen.
Beispiel: 
Wir multiplizieren die gemeinsamen Primfaktoren und .
Häufig gestellte Fragen zum Thema Primfaktorzerlegung
Eine Primfaktorzerlegung ist ein Produkt aus Primzahlen.
Die Primfaktorzerlegung einer Zahl ist ein Produkt aus Primzahlen, dessen Wert der Zahl entspricht.
Eine Primfaktorzerlegung besteht aus allen Primzahlen, die Teiler einer Zahl sind. Wir müssen also alle Primzahlen finden, die die Zahl teilen.
Um eine Primfaktorzerlegung durchzuführen, können wir die Zahl nach und nach auf die Teilbarkeit durch verschiedene Primzahlen überprüfen. Haben wir eine Primzahl gefunden, die Teiler ist, dann bestimmen wir den Quotienten und rechnen damit weiter, bis der Quotient selbst eine Primzahl ist.
Bei der Berechnung einer Primfaktorzerlegung können wir eine Tabelle zur Hilfe nehmen, in der wir nach und nach durch die gefundenen Primfaktoren teilen, bis eine Primzahl übrig bleibt.
Damit die Primfaktorzerlegung einer Zahl möglichst einfach gelingt, überprüfen wir zunächst die Teilbarkeit durch die kleinste Primzahl . Ist diese kein Teiler (mehr), gehen wir zur nächstgrößeren Primzahl weiter, dann prüfen wir die Teilbarkeit durch etc. so lange, bis wir alle Primfaktoren gefunden haben.
Dabei helfen auch die Teilbarkeitsregeln.
Die Primfaktorzerlegung wird beispielsweise beim Kürzen von Brüchen oder bei der Bestimmung des größten gemeinsamen Teilers und des kleinsten gemeinsamen Vielfachen genutzt.
Es gilt: Das kleinste gemeinsame Vielfache zweier Zahlen ist das Produkt aller Primfaktoren, die in einer der Primfaktorzerlegungen der beiden Zahlen vorkommen. Zahlen, die in beiden Zerlegungen vorkommen, zählen dabei immer nur einmal.
Es gilt: Der größte gemeinsame Teiler zweier Zahlen ist das Produkt aller Primfaktoren, die gleichzeitig in den Primfaktorzerlegungen beider Zahlen vorkommen.