Rechteck Mathe – einfach erklärt

Rechtecke sind geometrische Figuren. Ein Rechteck hat vier Seiten, vier Ecken und somit auch vier Winkel. Alle Winkel sind rechte Winkel, sie sind also genau groß.
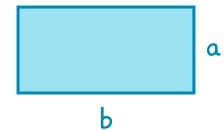
Die gegenüberliegenden Seiten des Rechtecks sind immer parallel und gleich lang. Die Rechteckseiten werden häufig mit den gleichen Buchstaben bezeichnet. In den meisten Fällen sind die Seiten eines Rechtecks mit den Buchstaben und beschriftet. Ein Rechteck hat somit eine Länge und eine Breite. Die längeren Seiten werden auch als Längsseiten des Rechtecks bezeichnet.
Bei Rechtecken müssen im Gegensatz zu Quadraten jedoch nicht alle vier Seiten gleich lang sein. Jedes Quadrat ist somit ein Rechteck, aber nicht jedes Rechteck ist ein Quadrat.

Quelle sofatutor.com

Da zwar alle Winkel gleich groß, aber nicht alle Seiten gleich lang sind, handelt es sich nicht um ein regelmäßiges Viereck. 

Die Diagonalen verbinden die gegenüberliegenden Ecken des Rechtecks. Sie sind genau gleich lang und halbieren sich gegenseitig.
Rechtecke haben zwei Symmetrieachsen. Die Symmetrieachsen halbieren sich gegenseitig. Eine Symmetrieachse geht von der Mitte der einen langen Seite zur Mitte der anderen langen Seite. Die andere Symmetrieachse geht von der Mitte der einen kurzen Seite zur Mitte der anderen kurzen Seite.

Es lassen sich verschiedene Größen des Rechtecks berechnen. Besonders wichtig sind der Umfang und der Flächeninhalt. Wir schauen uns aber auch an, wie die Berechnung für die Diagonalen eines Rechtecks lautet.
Da ein Rechteck eine Figur und kein Körper ist, besitzt es kein Volumen, das berechnet werden kann.

Um den Umfang eines Rechtecks zu berechnen, werden alle Seitenlängen miteinander addiert. Da zwei Seiten immer gleich lang sind, können wir also und addieren:

Beispiel – Umfang eines Rechtecks
Der Umfang eines Rechtecks mit den Seitenlängen und soll berechnet werden:

Um den Flächeninhalt eines Rechtecks zu berechnen, multiplizierst du die Seitenlängen zweier verschieden langer Seiten:

Beachte, dass die Einheit vom Flächeninhalt immer ein Quadrat besitzt.

Beispiel – Flächenberechnung Rechteck
Die Fläche eines Rechtecks mit den Seitenlängen und soll berechnet werden:

Ist der Umfang und eine Seite gegeben, können wir die andere Seite mit der folgenden Formel berechnen:

Ist der Flächeninhalt und eine Seite gegeben, können wir die andere Seite mit der folgenden Formel berechnen:

Beispiel – Seiten eines Rechtecks berechnen
Gegeben: und
Gesucht:
Rechnung:

Gegeben: und
Gesucht:
Rechnung:

Zur Berechnung der Diagonalen eines Rechtecks wird der Satz des Pythagoras benötigt, weil die Länge, die Breite und die Diagonale ein rechtwinkliges Dreieck bilden. Es gilt:

Dabei sind die Länge des Rechtecks, die Breite des Rechtecks und die Diagonale.

Beispiel – Diagonale berechnen
Gegeben: und
Gesucht:
Rechnung:

Das Rechteck gehört wie das Quadrat zu den besonderen Vierecken. Weitere besondere Vierecke sind das Parallelogramm, die Raute, das Trapez und das Drachenviereck. Vergleichen wir die Merkmale des Rechtecks mit den Merkmalen der anderen Vierecke, stellen wir fest:

• Jedes Quadrat ist ein Rechteck.
• Ein Rechteck mit vier gleich langen Seiten ist auch ein Quadrat, eine Raute und ein Drachenviereck.
• Jedes Rechteck ist ein Parallelogramm.
• Ein Parallelogramm mit rechten Winkeln ist auch ein Rechteck.
• Jedes Rechteck ist ein Trapez.
• Ein Trapez mit rechten Winkeln ist auch ein Rechteck.
• Jedes Rechteck ist ein allgemeines Viereck.

Einen Überblick zu den Zusammenhängen der einzelnen Vierecke bietet das Haus der Vierecke.

Formen können auch aus verschiedenen Rechtecken zusammengesetzt sein. Dann sprechen wir von zusammengesetzten Rechtecken. Das folgende linke Rechteck ist aus drei Rechtecken zusammengesetzt:

Um den Flächeninhalt einer aus Rechtecken zusammengesetzten Figur zu berechnen, können wir diese zerlegen. Die oben dargestellte zusammengesetzte Figur kann in drei Rechtecke (, und ) zerlegt werden. Dann können wir die Flächeninhalte der Rechtecke einzeln ausrechnen. Der Flächeninhalt der gesamten Fläche ist die Summe der drei Teilflächen.

Beispiel zusammengesetzte Figur
Die oben dargestellte Fläche kann in drei Rechtecke aufgeteilt werden. Die einzelnen Rechtecke haben die Flächeninhalte:

Die zusammengesetzte Form hat also den Flächeninhalt: