Normalverteilung – einfach erklärt
Die Normalverteilung ist eine wichtige stetige Wahrscheinlichkeitsverteilung mit Mittelwert und Standardabweichung als entscheidenden Kenngrößen. Entdecke die gaußsche Glockenkurve und wie sie Daten darstellt. Dies und mehr findest du im Text!
Inhaltsverzeichnis zum Thema Normalverteilung
Normalverteilung – Erklärung und Eigenschaften
Die Normalverteilung wird zur Darstellung und Untersuchung von Daten und Beobachtungen genutzt. Sie wird auch Gaußverteilung genannt.
Normalverteilung – Definition: Die Normalverteilung ist eine der wichtigsten Wahrscheinlichkeitsverteilungen in der Stochastik. Bei der Normalverteilung handelt es sich um eine stetige Wahrscheinlichkeitsverteilung. Die betrachteten Zufallsgrößen können also nicht nur diskrete Werte annehmen.
Darin liegt der entscheidende Unterschied zwischen der Normalverteilung und der Binomialverteilung. Die Binomialverteilung existiert nur für ganzzahlige Werte, während die Normalverteilung auch für beliebige reelle Zahlen existiert.
Die Wahrscheinlichkeitsverteilung einer normalverteilten Zufallsgröße ![]() kann anhand der Kenngrößen Mittelwert
kann anhand der Kenngrößen Mittelwert ![]() und Standardabweichung
und Standardabweichung ![]() durch eine Dichtefunktion beschrieben werden:
durch eine Dichtefunktion beschrieben werden:
![]()
Normalverteilung – Beispiel: Die Verteilung von Körpergrößen der über ![]() -jährigen Personen in Deutschland (differenziert nach dem biologischen Geschlecht) ließe sich folgendermaßen darstellen:
-jährigen Personen in Deutschland (differenziert nach dem biologischen Geschlecht) ließe sich folgendermaßen darstellen:

Sie folgen in etwa einer Normalverteilung. Dabei kann die Körpergröße nicht nur diskrete Werte wie ![]() oder
oder ![]() annehmen, sondern auch Werte wie
annehmen, sondern auch Werte wie ![]() oder
oder ![]() .
.
An der typischen Form der Kurve ist erkennbar, warum die Normalverteilung auch als (gaußsche) Glockenkurve bezeichnet wird.
Normalverteilung – Merkmale:
- Graph der Dichtefunktion der Normalverteilung folgt einem symmetrischen Kurvenverlauf.
- Median und Mittelwert sind identisch.
Normalverteilung – Formel
Die Normalverteilung hängt von dem Mittelwert ![]() , der Varianz
, der Varianz ![]() und der Standardabweichung
und der Standardabweichung ![]() ab. Dabei gilt:
ab. Dabei gilt:
Die Normalverteilung wird kurz auch als ![]() bezeichnet.
bezeichnet.
Normalverteilung – Erwartungswert
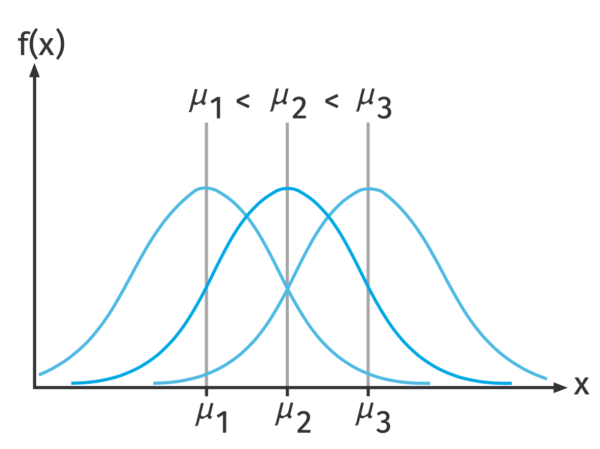
Der Erwartungswert entspricht bei einer normalverteilten Zufallsgröße dem Mittelwert ![]() , bei dem das Maximum der Normalverteilung liegt. Wird
, bei dem das Maximum der Normalverteilung liegt. Wird ![]() größer, verschiebt sich die Kurve nach rechts. Wird
größer, verschiebt sich die Kurve nach rechts. Wird ![]() kleiner, verschiebt sich die Kurve nach links.
kleiner, verschiebt sich die Kurve nach links.
Normalverteilung – Varianz und Stadardabweichung
Die Varianz ![]() und die Standardabweichung
und die Standardabweichung ![]() beeinflussen die Form der Kurve. Sie beschreiben die Streuung der Daten um den Mittelwert: Je größer die Werte, desto stärker streuen die Daten um den Mittelwert.
beeinflussen die Form der Kurve. Sie beschreiben die Streuung der Daten um den Mittelwert: Je größer die Werte, desto stärker streuen die Daten um den Mittelwert.
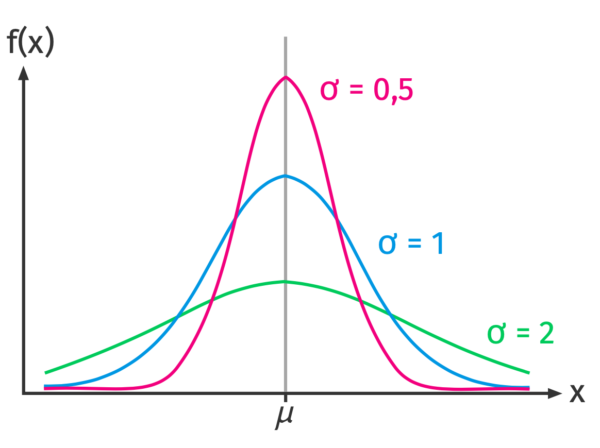
Das bedeutet für den Kurvenverlauf: Wird ![]() bzw.
bzw. ![]() größer, wird die Kurve gestaucht (breiter). Wird
größer, wird die Kurve gestaucht (breiter). Wird ![]() kleiner, wird die Kurve gestreckt (schmaler).
kleiner, wird die Kurve gestreckt (schmaler).
Normalverteilung – Dichtefunktion, Verteilungsfunktion und Verteilungstabelle
Die Dichtefunktion der allgemeinen Normalverteilung lautet:
![]()
Eigenschaften der Dichtefunktion der Normalverteilung:
- Sie ist symmetrisch zu
 .
. 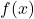 ist nie
ist nie 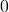 .
.- Maximum liegt beim Erwartungswert
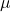 .
. - stetig
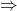 definiert von
definiert von 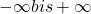
- Sie hat zwei Wendepunkte, die genau eine Standardabweichung vom Erwartungswert entfernt liegen (
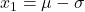 ;
; 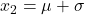 ).
).
Die Fläche unter der Dichtefunktion wird durch die Verteilungsfunktion der Normalverteilung angegeben und wird daher als bestimmtes Integral im Intervall von ![]() bis
bis ![]() berechnet.
berechnet.
Die Formel für die Verteilungsfunktion lautet:
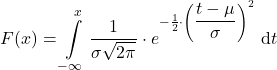
Mit der Verteilungsfunktion lässt sich die sogenannte Intervallwahrscheinlichkeit berechnen. Das bedeutet die Wahrscheinlichkeit, dass ein Wert in einem bestimmten Intervall liegt. Es gilt:
![]()
Diese Verteilungsfunktion muss jedoch nicht berechnet werden. Es existieren sogenannte Verteilungstabellen, aus denen sich die Ergebnisse einfach ablesen lassen. In der ersten Spalte lesen wir den Wert bis zur ersten Nachkommastelle ab. Alle weiteren Nachkommastellen werden in der ersten Zeile abgelesen. An der Schnittstelle der entsprechenden Zeile und Spalte findet sich die gesuchte Wahrscheinlichkeit.
Standardnormalverteilung
Es existieren unendlich viele verschiedene Normalverteilungen mit verschiedenen Erwartungswerten und Varianzen. Für jede bräuchten wir zur Berechnung eine eigene Verteilungstabelle, was nicht möglich ist. Daher gibt es die Standardnormalverteilung.
Standardnormalverteilung: ![]()
Dichtefunktion: ![]()
Jede Normalverteilung kann in die Standardnormalverteilung transformiert werden. Es wird somit nur noch eine Verteilungstabelle benötigt, aus der alle Wahrscheinlichkeiten abgelesen werden können.
Eine Normalverteilung kann in die Standardnormalverteilung transformiert werden, indem zuerst der Erwartungswert abgezogen und dann durch die Standardabweichung ![]() geteilt wird. Die Gleichung, um eine Normalverteilung in eine Standardnormalverteilung zu transformieren, lautet:
geteilt wird. Die Gleichung, um eine Normalverteilung in eine Standardnormalverteilung zu transformieren, lautet:
![]()
Somit gilt: ![]()
Die standardisierte Form wird dabei als ![]() statt
statt ![]() bezeichnet, um Verwechslungen zu vermeiden.
bezeichnet, um Verwechslungen zu vermeiden.
Somit kann die Intervallwahrscheinlichkeit auch mit der Standardnormalverteilung berechnet werden:
![]()
In der Tabelle sind nur positive Werte gelistet. Bei negativen Werten muss eine kurze Umrechnung durchgeführt werden:
![]()
Aufgrund der heutzutage in der Schule verwendeten Taschenrechner ist eine Transformation nicht unbedingt notwendig.

Beispiel
Die Wahrscheinlichkeit, dass ![]() kleiner als
kleiner als ![]() ist, berechnen wir als:
ist, berechnen wir als:
![]()
Normalverteilung interpretieren
Aus einer Normalverteilung kann abgelesen werden, mit welcher Wahrscheinlichkeit ein bestimmter Wert oder ein bestimmter Bereich an Werten auftritt. Am Maximum lässt sich der Mittelwert ![]() bzw. der Erwartungswert der Daten ablesen. Im Bereich innerhalb einer Standardabweichung um den Erwartungswert liegen ungefähr
bzw. der Erwartungswert der Daten ablesen. Im Bereich innerhalb einer Standardabweichung um den Erwartungswert liegen ungefähr ![]() aller Werte. Im Bereich innerhalb von zwei Standardabweichungen um den Mittelwert liegen um
aller Werte. Im Bereich innerhalb von zwei Standardabweichungen um den Mittelwert liegen um ![]() aller Werte und im Bereich innerhalb von drei Standardabweichungen um den Mittelwert liegen ca.
aller Werte und im Bereich innerhalb von drei Standardabweichungen um den Mittelwert liegen ca. ![]() aller Werte.
aller Werte.

Betrachten wir dafür noch einmal die Normalverteilung der Körpergrößen von Frauen. Angenommen es gelten die folgenden Werte:
![]()
![]()
Dann können wir Folgendes interpretieren:
| Wert | Erklärung | Beispiel |
|---|---|---|
| Mittelwert | Die durchschnittliche Körpergröße beträgt |
|
| Standardabweichung | Die Standardabweichung der Körpergröße beträgt |
|
| Intervall von |
||
| Intervall von |
||
| Intervall von |
||
Normalverteilung – Wahrscheinlichkeit berechnen
Betrachten wir die Normalverteilung am Beispiel der Brenndauer einer Kerze in Minuten. Gegeben sind die Werte:
![]()
![]()
Wir nehmen an, dass die Brenndauer der Kerze normalverteilt ist.
Frage
Mit welcher Wahrscheinlichkeit brennt die Kerze zwischen ![]() und
und ![]() Minuten?
Minuten?
Lösung
Gesucht ist: ![]()
Zunächst standardisieren und vereinfachen wir die Normalverteilung:
![]()
![]()
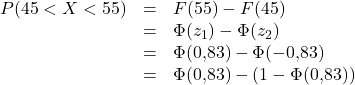
Nun muss der Wert für ![]() aus der Verteilungstabelle abgelesen werden:
aus der Verteilungstabelle abgelesen werden:
![]()
Die vorangegangenen Schritte können einfach mithilfe des Taschenrechners gelöst werden.
Diesen Wert können wir nun in die Gleichung einsetzen und erhalten:
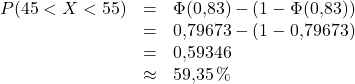
Antwortsatz
Die Wahrscheinlichkeit, dass die Kerze zwischen ![]() und
und ![]() Minuten brennt, beträgt rund
Minuten brennt, beträgt rund ![]() .
.
Normalverteilung – Anwendung
Die Normalverteilung wird meist dann verwendet, wenn eine große Stichprobe vorliegt. Wenn die eigentliche Verteilung der Stichproben unbekannt ist, dient die Normalverteilung als Hilfsmittel zur Darstellung der Daten. Sie wird in vielen verschiedenen naturwissenschaftlichen, gesellschaftswissenschaftlichen und wirtschaftswissenschaftlichen Bereichen angewandt. Ein paar Beispiele sind:
- Biologie: Körpergrößen einer Personengruppe
- Meteorologie: Regenmenge
- Physik: Messfehler
- Gesellschaftswissenschaften: Einkommen
- Finanzmarkt: Preisänderung von Aktien
Auch ein typisches Beispiel aus dem Mathematikunterricht, die Summe der Augenzahlen beim Würfeln mit mehr als einem Würfel, kann mit einer Normalverteilung angenähert werden.
Häufig gestellte Fragen zum Thema Normalverteilung

