Parallelogramm – Definition, Formeln und Beispiele
Ein Parallelogramm ist ein Viereck mit parallelen, gleich langen Seiten und gegenüberliegenden Winkeln. Erfahre mehr über Symmetrie, Formeln für Umfang und Fläche sowie praktische Anwendungen in Architektur und Design. Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Parallelogramm
Das Quiz zum Thema: Parallelogramm
Was ist ein Parallelogramm?
Frage 1 von 5
Welche Eigenschaft haben gegenüberliegende Seiten in einem Parallelogramm?
Frage 2 von 5
Wie berechnet sich der Umfang eines Parallelogramms?
Frage 3 von 5
Wie sieht es mit den Winkeln in einem Parallelogramm aus?
Frage 4 von 5
Welche besondere Form des Parallelogramms hat vier rechte Winkel?
Frage 5 von 5
Wie willst du heute lernen?
Parallelogramm – Eigenschaften
Ein Parallelogramm ist eine geometrische Figur, bei der gegenüberliegende Seiten parallel und gleich lang sind. Wir definieren es als Viereck mit zwei Paaren paralleler Seiten.
Die Eigenschaften eines Parallelogramms sind:
- Gegenüberliegende Seiten sind parallel.
- Gegenüberliegende Seiten sind gleich lang.
- Gegenüberliegende Winkel sind gleich groß.
- Benachbarte Winkel ergeben zusammen
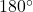 .
. - Die Diagonalen halbieren sich gegenseitig.
- Diese Eigenschaften müssen beim Zeichnen von Parallelogrammen beachtet werden.
Betrachten wir folgendes Parallelogramm:

Die Beschriftung der Ecken erfolgt, wie bei Vierecken üblich, gegen den Uhrzeigersinn mit den Großbuchstaben ![]() bis
bis ![]() . Die auf die jeweilige Ecke folgenden Seiten werden mit den entsprechenden Kleinbuchstaben
. Die auf die jeweilige Ecke folgenden Seiten werden mit den entsprechenden Kleinbuchstaben ![]() bis
bis ![]() gekennzeichnet. Die Winkel werden mit den griechischen Buchstaben
gekennzeichnet. Die Winkel werden mit den griechischen Buchstaben ![]() ,
, ![]() ,
, ![]() und
und ![]() beschriftet.
beschriftet.
Für dieses Parallelogramm gilt also:
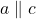 und
und 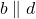
 und
und 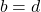
 und
und 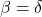

Die Innenwinkelsumme, kurz Winkelsumme, eines Parallelogramms beträgt immer ![]() .
.
Parallelogramm – besondere Fälle
Es gibt verschiedene Arten von Parallelogrammen, die jeweils eine Besonderheit aufweisen:
- Rechteck: Ein Parallelogramm mit vier rechten Winkeln ist ein Rechteck.
- Raute (Rhombus): Ein Parallelogramm mit vier gleich langen Seiten ist eine Raute. Eine Raute ist also ein gleichseitiges Parallelogramm.
- Quadrat: Ein Parallelogramm mit vier rechten Winkeln und vier gleich langen Seiten ist ein Quadrat.
Zudem ist jedes Parallelogramm ein spezielles Trapez mit zwei parallelen Seitenpaaren.
Entsprechend wird das Parallelogramm im Haus der Vierecke eingeordnet.
Parallelogramm – Symmetrie
Jedes Parallelogramm ist punktsymmetrisch. Der Schnittpunkt der beiden Diagonalen ist das Symmetriezentrum des Parallelogramms.
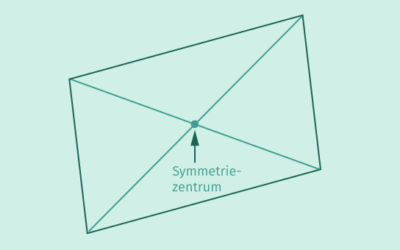
Achsensymmetrisch ist ein Parallelogramm im Allgemeinen jedoch nicht. Nur die speziellen Parallelogramme Raute und Rechteck haben zwei Symmetrieachsen.
Parallelogramm – Formeln
Nun schauen wir uns einige Formeln an, um verschiedene Größen in einem Parallelogramm zu berechnen.
Umfang:
Für den Umfang eines Parallelogramms gilt die Formel:
![]()
Es werden also alle Seiten addiert und die Formel durch die Tatsache vereinfacht, dass die gegenüberliegenden Seiten gleich lang sind.
Flächeninhalt:
Die Fläche eines Parallelogramms berechnet sich aus einer Seite und der zugehörigen Höhe. Nimmt man die Seite ![]() als Grundseite, gilt die Formel:
als Grundseite, gilt die Formel:
![]()
Ebenso gilt für die Seite ![]() :
:
![]()
Die Höhe beschreibt dabei den kürzesten Abstand von der jeweiligen Seite zur gegenüberliegenden Seite.

Beispiel:
Gegeben ist ein Parallelogramm mit den Seiten ![]() und
und ![]() und einer Höhe
und einer Höhe ![]() . Das Einsetzen in die Formeln für den Umfang und die Flächenberechnung liefert:
. Das Einsetzen in die Formeln für den Umfang und die Flächenberechnung liefert:
![]()
![]()
Sind der Flächeninhalt und eine Seite des Parallelogramms gegeben, kann die zugehörige Höhe durch Umstellen der Flächenformel berechnet werden:
![]()
Wir können die Formel auch nach der Seite ![]() umstellen und so über Flächeninhalt und Höhe die Länge der Seite berechnen:
umstellen und so über Flächeninhalt und Höhe die Länge der Seite berechnen:
![]()
Parallelogramm – Beispiele im Alltag
Parallelogramme finden sich in vielen Bereichen des Alltags. Einige Beispiele aus dem Bereich Architektur sind Muster von Bodenbelägen, Fenster oder ganze Gebäude. Auch auf Spielkarten oder Landesflaggen sind Parallelogramme zu finden.
Häufig gestellte Fragen zum Thema Parallelogramm









Alle Artikel aus dem Fach Mathematik