Quadratische Ergänzung – Definition, Erklärung und Beispiele

Erfahre, wie quadratische Ergänzung quadratische Terme umformt und binomische Formeln anwendet. Löse Gleichungen und finde Scheitelpunkte mithilfe dieses Verfahrens. Dies und vieles mehr findest du im folgenden Text!

Inhaltsverzeichnis zum Thema Quadratische Ergänzung

Quadratische Ergänzung im Überblick

  • Die quadratische Ergänzung ist in der Mathematik ein Verfahren zur Umformung quadratischer Terme.
  • Zum Einsatz kommt die quadratische Ergänzung daher beim Umgang mit quadratischen Funktionen, z. B. um den Scheitelpunkt oder die Nullstellen zu bestimmen.
  • Bei der quadratischen Ergänzung spielen die binomischen Formeln eine wichtige Rolle.
Quadratische Ergänzung: Lernvideo

Quelle sofatutor.com

Quadratische Ergänzung – einfach erklärt

Ein quadratischer Term ist ein Term der Form ax^2+bx+c mit a\neq0, also mit dem höchsten Exponenten 2. Bei der quadratischen Ergänzung wird ein quadratischer Term nun so umgeformt, dass die 1. oder 2. binomische Formel angewendet werden kann. Beispielsweise hilft die quadratische Ergänzung, wenn der Term 4x^2+16x-12 in den gleichwertigen Term 4(x+2)^2 - 28 umgeformt werden soll. Dazu sagen wir auch: „Der Term wird teilweise faktorisiert.“

Im Folgenden wird das Vorgehen bei der quadratischen Ergänzung Schritt für Schritt erklärt.
Gegeben ist der quadratische Term 4x^2+16x-12.

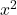  • Vor dem x^2 steht ein Faktor, der zunächst ausgeklammert wird:
    4x^2+16x-12 = 4(x^2+4x-3)
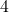  • Der Faktor vor dem x, hier also 4, wird durch 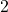2 dividiert:
    4:2 = 2
  • Dieser Wert wird nun quadriert:
    2^2 = 4
  • Nun wird diese 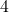4 zu dem Term in der Klammer addiert und anschließend wieder subtrahiert. Insgesamt wird so 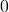0 addiert, der Wert des Terms ändert sich dadurch nicht.
    4(x^2+4x\underbrace{{}+{}4-4}_{+0}-~3)
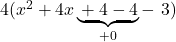
  • Für die ersten drei Summanden in der Klammer kann nun die 1. binomische Formel angewendet werden:
    x^2 + 4x+4 = (x+2)^2
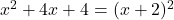
  • Diese Umformung wird in den gesamten Term eingesetzt und weiter zusammengefasst:
    \begin{array}{rcl} 4(x^2+4x+4-4-3)& = & 4((x+2)^2 -4-3)\\ & = & 4((x+2)^2 -7) \\ & = & 4(x+2)^2 -28 \end{array}

Schritte der quadratischen Ergänzung

Die quadratische Ergänzung für einen quadratischen Term ax^2+bx+c mit a\neq0 läuft wie folgt ab:

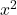  • Vorfaktor a vor dem x^2 ausklammern
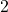  • Faktor vor dem x durch 2 dividieren und dann quadrieren
  • Ergebnis zum Term in der Klammer addieren und subtrahieren („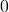0 addieren“)
  • Binomische Formel anwenden
  • Term zusammenfassen

Anwendung der quadratischen Ergänzung

Die quadratische Ergänzung kommt vor allem beim Lösen von Gleichungen oder beim Bestimmen von Nullstellen zum Einsatz.

Quadratische Ergänzung – quadratische Gleichungen lösen

Eine quadratische Gleichung der Form ax^2+bx+c = 0 lässt z. B. mithilfe der pq-Formel oder der Mitternachtsformel lösen. Es ist aber auch möglich, die Gleichung mit der quadratischen Ergänzung zu lösen. Dafür wird der quadratische Term wie oben gezeigt umgeformt, danach kann die quadratische Klammer isoliert und die Wurzel gezogen werden.
Im folgenden Beispiel schauen wir uns einmal an, wie das funktioniert:
Wir suchen die Lösungen der Gleichung 2x^2+8x-10 = 0.
Wir formen um:
\begin{array}{lrcll} &2x^2+8x-10 & = & 0 & \vert\ \text{Vorfaktor ausklammern}\\ \Leftrightarrow & 2(x^2+4x-5) & = & 0 & \vert\ 0~\text{addieren} \\ \Leftrightarrow & 2(x^2+4x+4-4-5) & = & 0 & \vert\ \text{1. binomische Formel anwenden} \\ \Leftrightarrow & 2((x+2)^2-9) & = & 0 & \vert\ \text{Klammer auflösen} \\ \Leftrightarrow & 2(x+2)^2-18 & = & 0 & \vert\ + 18 \\ \Leftrightarrow & 2(x+2)^2 & = & 18 & \vert\ :2 \\ \Leftrightarrow & (x+2)^2 & = & 9 & \vert\ \sqrt{~} \\ \Leftrightarrow & x+2 & = & \pm 3 & \vert\ -2\\ \end{array}

Daraus ergeben sich die Lösungen x_1=-2-3 = -5 und x_2=-2+3 = 1.

Quadratische Ergänzung – Scheitelpunktform einer quadratischen Funktion

Liegt eine quadratische Funktion in der Form f(x) = ax^2+bx+c mit a\neq0 vor, sagen wir dazu Normalform. Durch Termumformung lässt sich der Funktionsterm auch in die Scheitelpunktform f(x) =a(x-d)^2+e umformen, wobei der Punkt S(d \vert e) der Scheitelpunkt der zugehörigen Parabel ist. Um einen Funktionsterm einer quadratischen Funktion von der Normalform in die Scheitelpunktform umzuformen, hilft die quadratische Ergänzung.

Wie dies funktioniert, schauen wir uns an einem Beispiel an:
Die Funktion f(x) = -0,5x^2+2x+4 soll in Scheitelpunktform umgeformt werden:
\begin{array}{rcl} -0,5x^2+2x+4& = & -0,5(x^2-4x-8)\\ & = & -0,5(x^2-4x+4-4-8)\\ & = & -0,5((x-2)^2-4-8)\\ & = & -0,5((x-2)^2-12)\\ & = & -0,5(x-2)^2+ 6\\ \end{array}

Aus der Scheitelpunktform f(x) = -0,5(x-2)^2 + 6 lassen sich die Koordinaten des Scheitelpunkts S(2 \vert 6) ablesen.

Häufig gestellte Fragen zum Thema Quadratische Ergänzung 

Die quadratische Ergänzung ist ein Vorgehen zum Umformen von quadratischen Termen.

Bei der quadratischen Ergänzung wird ein quadratischer Term so umgeformt, dass die erste oder zweite binomische Formel angewendet werden kann und der Term so teilweise faktorisiert wird.

Die quadratische Ergänzung wird beim Lösen von quadratischen Gleichungen oder beim Bestimmen von Nullstellen und Scheitelpunkt von quadratischen Funktionen verwendet.

Die quadratische Ergänzung hilft beim Umformen von quadratischen Termen. Außerdem lässt sich der Funktionsterm einer Parabel mithilfe der quadratischen Ergänzung in die Scheitelpunktform bringen.

Sowohl die pq-Formel als auch die quadratische Ergänzung helfen beim Lösen von quadratischen Gleichungen. Die pq-Formel lässt sich aus der quadratischen Ergänzung herleiten. Bei anderen Anwendungen der quadratischen Ergänzungen, wie dem Umformen einer quadratischen Funktion in die Scheitelpunktform, wird eher die quadratische Ergänzung genutzt, weil man mit dieser direkter auf die Scheitelpunktform kommt.

Leave A Comment

Alle Artikel aus dem Fach Mathematik