Statistische Lageparameter – arithmetisches Mittel, Median und Modalwert
Statistische Lageparameter wie arithmetisches Mittel, Median und Modalwert geben dir wichtige Einblicke in Datendistributionen. Entdecke ihre Definitionen und Unterschiede sowie praktische Anwendungen! Dies und vieles mehr findest du im folgenden Text.
Inhaltsverzeichnis zum Thema Lageparameter der Statistik
Lageparameter der Statistik im Überblick
Quelle sofatutor.com
Lageparameter – Definition
In der Statistik gibt es verschiedene Kennwerte, um Daten zu beschreiben und zu interpretieren. Wir unterscheiden dabei Lageparameter und Streuungsparameter. Lageparameter sind Kennwerte dafür, in welchem Bereich sich Daten befinden. Streuungsparameter sind Kennwerte für die Abweichung der Daten von den Lageparametern. Was die wichtigsten Lageparameter sind und wie man diese berechnen kann, schauen wir uns in den nächsten Absätzen an dem folgenden Beispieldatensatz an.
Beispiel Datensatz
Die Noten einer Schulklassen sind folgendermaßen verteilt:
| Note |  |
 |
 |
 |
 |
 |
| Anzahl | |
|
|
|
|
|
Arithmetisches Mittel – Definition
Mit dem arithmetischen Mittel werden Werte aus einer Datenreihe zu einem Durchschnittswert zusammengefasst. Das arithmetische Mittel wird auch als Durchschnitt, (empirischer) Mittelwert oder arithmetischer Mittelwert bezeichnet. Das Symbol für das arithmetische Mittel ist 
(ausgesprochen: 
quer).
Der Wert des arithmetischen Mittels muss im Datensatz nicht als Wert vorkommen.
Arithmetisches Mittel (Mittelwert) berechnen
Für die Berechnung des arithmetischen Mittels werden zunächst alle Werte addiert. Die Summe wird im Anschluss durch die Anzahl der Werte dividiert.
In der mathematischen Schreibweise wird die Anzahl der Werte mit 
abgekürzt. Die einzelnen Werte werden als mit dem Index bis durchnummeriert. Die Formel für das arithmetische Mittel (Mittelwert) lautet dann:
Mit dieser Formel kann man also den Durchschnitt einer Datenreihe berechnen.
Arithmetisches Mittel – Beispiel:
Betrachten wir das Beispiel der Schulklasse. Das arithmetische Mittel gibt hier den Notendurchschnitt an. Um das arithmetische Mittel zu berechnen, addieren wir zunächst alle Noten einzeln. Im Anschluss teilen wir die Summe durch die Anzahl der Kinder:
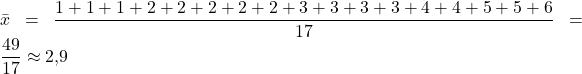
Der Notendurchschnitt der Klasse ist gerundet 
.
Wie du siehst, kommt der Wert nicht im Datensatz vor.
Median – Mathe
Als Median wird der Wert bezeichnet, der genau in der Mitte einer Datenreihe liegt. Er teilt die Datenreihe somit in zwei Teile mit gleich vielen Werten. Diese Teile werden auch als untere und obere Hälfte bezeichnet. Dabei sind alle Werte in der unteren Hälfte kleiner oder gleich dem Median. Alle Werte in der oberen Hälfte sind größer oder gleich dem Median. Das Symbol für den Median ist 
(ausgesprochen: Tilde).
Median bestimmen
Um den Median zu bestimmen, werden die Werte zunächst ihrer Größe nach sortiert.
Im Anschluss wird der größte und kleinste Wert gestrichen.
Bei einer ungeraden Anzahl von Daten wird das so lange gemacht, bis nur noch ein Wert übrig bleibt. Dieser Wert ist der Median.
Bei einer geraden Anzahl an Werten bleiben am Ende zwei Werte übrig. Der Median ist das arithmetische Mittel dieser beiden mittleren Werte.
Bei einer geraden Anzahl an Daten kann es wie beim arithmetischen Mittel so sein, dass der Wert des Medians nicht als Wert in der Datenreihe vorkommt.
Es existiert keine Formel, um den Median zu berechnen.
Beispiel – ungerade Anzahl an Werten
Um den Median der Noten zu bestimmen, müssen wir zunächst alle Werte der Größe nach sortieren:
Im Anschluss streichen wir immer jeweils den kleinsten und größten Wert, bis nur noch ein Wert, der Median, übrig bleibt:
Der Median ist also .
Beispiel – gerade Anzahl an Werten
Zunächst sortieren wir alle Werte der Größe nach und streichen immer jeweils den kleinsten und größten Wert, bis nur noch zwei Werte übrig bleiben:
Hier siehst du, dass der Median nicht als Wert in der Datenreihe vorkommt.
Modalwert – Mathe
Der Wert, der am häufigsten auftritt, wird als Modalwert oder Modus bezeichnet. Um den Modalwert aus Datensätzen zu bestimmen, werden die Daten geordnet und dann kann geschaut werden, welcher Wert am häufigsten auftritt. Es existiert keine Formel, um den Modalwert zu berechnen. Er kann jedoch auch aus Säulendiagrammen abgelesen werden. Dort entspricht er dem Wert mit der höchsten Säule.
Beispiel:
Die Note kommt am häufigsten (-mal) in diesem Datensatz vor. Sie ist somit der Modalwert dieses Datensatzes.
Arithmetisches Mittel, Median und Modalwert – Unterschiede und Verwendung
Das arithmetische Mittel, der Median und der Modalwert sind Lageparameter. Sie unterscheiden sich jedoch in einigen entscheidenden Punkten und werden deshalb verschieden angewandt.
Das arithmetische Mittel ist der durchschnittliche Wert der Datenreihe. Der Median teilt hingegen die Datenreihe in zwei Teile mit gleich vielen Werten, liegt also genau in der Mitte. Median und arithmetisches Mittel (Mittelwert) können genau gleich groß sein. Ist das der Fall, handelt es sich um eine symmetrische Verteilung.
Der Median kann jedoch auch größer oder kleiner als das arithmetische Mittel sein. Ist der Median größer als das arithmetische Mittel, sprechen wir von einer linksschiefen Verteilung, ist er kleiner, sprechen wir von einer rechtsschiefen Verteilung.
Ein weiterer Unterschied der beiden Werte ist die Sensibilität gegenüber Ausreißern. So ist das arithmetische Mittel sehr sensibel gegenüber Ausreißern. Der Median hingegen ist robust gegenüber Ausreißern.
Der Modalwert wiederum gibt den Wert an, der am häufigsten in der Datenreihe vorkommt. Dieser Wert kann überall im Datensatz liegen und muss nicht mit dem arithmetischen Mittel oder dem Median übereinstimmen. Im Gegensatz zu den anderen beiden Werten kann er auch für kategorische Werte (beispielsweise Lieblingsfarbe der Kinder einer Klasse), die nicht geordnet werden können, verwendet werden.
Sind alle drei Werte gleich, sprechen wir von einer symmetrischen, unimodalen Verteilung.
Häufig gestellte Fragen zum Thema Statistische Lageparameter
Lageparameter geben in der Statistik die zentrale Lage der Verteilung von Daten an. Die wichtigsten Lageparameter sind das arithmetische Mittel, der Median und der Modalwert.
Das arithmetische Mittel gibt den Durchschnittswert einer Datenreihe an. Es ist auch unter den Begriffen Mittelwert oder Durchschnitt bekannt.
Um das arithmetische Mittel zu berechnen, werden alle Werte einer Datenreihe addiert. Die Summe wird danach durch die Anzahl an Werten geteilt. Die Formel für das arithmetische Mittel lautet:
Der Mittelwert ist ein anderer Begriff für das arithmetische Mittel, er gibt also ebenfalls den Durchschnittswert einer Datenreihe an.
Der Mittelwert ist eine andere Bezeichnung für das arithmetische Mittel und wird mit der Formel: 
berechnet.
Da auch der Durchschnitt nur ein anderer Begriff für das arithmetische Mittel ist, wird er ebenfalls mit der Formel 
berechnet.
Der Median ist der Wert einer Datenreihe, der genau in der Mitte liegt. Dabei müssen die Werte der Datenreihe der Größe nach sortiert sein. Handelt es sich um eine gerade Anzahl an Werten, ist der Median das arithmetische Mittel der beiden mittleren Werte.
Es existiert keine Formel zur Berechnung des Medians. Um den Median zu bestimmen, werden die Werte zunächst der Größe nach sortiert. Im Anschluss wird immer der jeweils größte und kleinste Wert gestrichen. Der Wert, der am Ende übrig bleibt, ist der Median. Bei einer geraden Anzahl an Werten bleiben zwei Werte am Ende übrig. Der Median ist in diesem Fall das arithmetische Mittel dieser beiden Werte.
Als Modalwert wird der Wert bezeichnet, der am häufigsten in einer Datenreihe auftritt.
Der Modalwert lässt sich nicht rechnerisch ermitteln. Um den Modalwert zu bestimmen, werden die Werte der Größe nach sortiert. So können wir sehen oder zählen, welcher Wert am häufigsten vorkommt.
Am häufigsten wird das arithmetische Mittel verwendet. Allerdings ist dieser Wert sehr sensibel gegenüber Ausreißern. Der Median hingegen ist robust gegenüber Ausreißern. Der Modalwert hat den großen Vorteil, dass er als Wert in der Datenreihe im Gegensatz zu den anderen beiden Werten tatsächlich immer vorkommt. Er berücksichtigt jedoch die anderen Werte der Datenreihe gar nicht. Je nachdem worauf man die Datenreihe untersuchen will, sind die verschiedenen Lageparameter unterschiedlich sinnvoll.
Der Median kann nur verwendet werden, wenn die Werte in eine Reihenfolge der Größe nach gebracht werden können. Sein Vorteil gegenüber dem arithmetischen Mittel ist die Robustheit gegenüber Ausreißern. Zudem teilt er die Datenreihe in zwei Teile mit exakt gleich vielen Werten.
Datenreihen lassen sich gut mit dem arithmetischen Mittel auswerten. So können Durchschnittsgröße, Durchschnittsnoten oder Ähnliches bestimmt werden.
Das arithmetische Mittel ist ein präziserer Wert, da er sehr sensibel gegenüber Ausreißern ist. Der Median hingegen ist deutlich robuster den Ausreißern gegenüber. Sollen die Ausreißer berücksichtigt werden, eignet sich das arithmetische Mittel besser. Sollen die Ausreißer einen geringeren Einfluss haben, eignet sich der Median besser.
Beide Begriffe beschreiben den gleichen Wert. Sie geben den Durchschnittswert einer Datenreihe an.
Der Mittelwert gibt den Durchschnittswert einer Datenreihe an, wohingegen der Median den mittleren Wert einer der Größe nach sortierten Datenreihe angibt.
Ja, beide Werte können gleich sein. Ist das der Fall, sprechen wir von einer symmetrischen Verteilung.
Ja, der Median kann größer als der Mittelwert sein. Ist das der Fall, sprechen wir von einer linksschiefen Verteilung. Bei einer rechtsschiefen Verteilung ist der Median kleiner als der Mittelwert.