Reelle Zahlen und irrationale Zahlen

Irrationale Zahlen haben unendlich viele nicht wiederholende Nachkommastellen, während reelle Zahlen sowohl rationale als auch irrationale Zahlen umfassen. Entdecke die Unterschiede zwischen ihnen und weitere Zahlenräume. Dies und vieles mehr findest du im folgenden Text!

Inhaltsverzeichnis zum Thema reelle Zahlen und irrationale Zahlen

Reelle Zahlen und irrationale Zahlen im Überblick

  • Irrationale Zahlen sind Dezimalzahlen mit unendlich vielen sich nicht wiederholenden Nachkommastellen.

  • Das Zeichen für die irrationalen Zahlen ist \mathbb{I}.
  • Die reellen Zahlen umfassen die Menge der rationalen Zahlen \mathbb{Q} und die Menge der irrationalen Zahlen \mathbb{I}.
  • Das Zeichen für die reellen Zahlen ist \mathbb{R}.
Reelle und irrationale Zahlen: Lernvideo

Quelle sofatutor.com

Arten von Zahlen

Es existieren verschiedene Arten von Zahlen, wir sprechen in der Mathematik auch von Zahlenbereichen oder Zahlenmengen. So kennst du bestimmt schon die natürlichen Zahlen, die negativen Zahlen, die ganzen Zahlen und die rationalen Zahlen. Im Folgenden wollen wir uns anschauen, was wir unter den irrationalen und den reellen Zahlen verstehen.

Irrationale Zahlen

Irrationale Zahlen sind Zahlen, die unendlich viele Nachkommastellen besitzen. Diese Nachkommastellen dürfen sich jedoch nicht periodisch wiederholen. So sind unter anderem Wurzeln aus natürlichen Zahlen, die keine Quadratzahlen sind, irrationale Zahlen. Das Symbol für die irrationalen Zahlen ist \mathbb{I}. 

Irrationale Zahlen – Beispiele

\sqrt{2}
\sqrt{7}
\pi
e

Unterschied rationale und irrationale Zahlen
Rationale Zahlen sind alle Zahlen, die als Bruch von zwei ganzen Zahlen dargestellt werden können. So sind zum Beispiel die Zahlen \frac{2}{5} und -365 rationale Zahlen.

-365 = \dfrac{-365}{1}

Rationale Zahlen können auch als Dezimalzahlen dargestellt werden. Sie besitzen entweder eine begrenzte Anzahl an Nachkommastellen (abbrechende Dezimalzahl) oder eine periodische Wiederholung der Zahlen nach dem Komma.

2,\!67 = \dfrac{267}{100}

Irrationale Zahlen haben eine unendliche Anzahl an Nachkommastellen, die sich nicht periodisch wiederholen. Somit lassen sie sich nicht als Bruch zweier ganzer Zahlen darstellen.

Natürliche Zahlen und ganze Zahlen lassen sich als Bruch schreiben, sie gehören also zu den rationalen Zahlen und nicht zu den irrationalen Zahlen.

Reelle Zahlen – Definition

Die Menge der reellen Zahlen umfasst die rationalen und irrationalen Zahlen. Jede rationale und jede irrationale Zahl ist also auch eine reelle Zahl. Das Zeichen für die reellen Zahlen ist \mathbb{R}.
Mathematisch können die reellen Zahlen als Vereinigung aus rationalen und irrationalen Zahlen geschrieben werden:

\mathbb{R} = \mathbb{Q} \cup \mathbb{I}

Dabei ist \mathbb{Q} das Zeichen für die rationalen Zahlen und \mathbb{I} das Zeichen für die irrationalen Zahlen.

Reelle Zahlen – Beispiele

Da die reellen Zahlen die Menge an rationalen Zahlen umfassen, sind alle ganzen und natürlichen Zahlen auch reelle Zahlen. So sind die Zahlen 2; \frac{-13}{12}; -399; 5,\!3;… reelle Zahlen. Aber auch alle irrationalen Zahlen sind reelle Zahlen. Die Wurzel aus 2 und die Wurzel aus 5 sind beispielsweise irrationale Zahlen und somit auch reelle Zahlen. Aber auch die irrationale Zahl e \approx 2,\!718 (eulersche Zahl) ist eine reelle Zahl.
Gehört eine Zahl zu einer Zahlengruppe, dann spricht man auch davon, dass diese ein Element dieser Gruppe ist. So können wir zum Beispiel sagen:

Die \sqrt{2} ist ein Element der reellen Zahlen.

Unterschied rationale und reelle Zahlen

Der Unterschied zwischen reellen und rationalen Zahlen liegt in der Zahlenmenge, die sie umfassen. Während die rationalen Zahlen nur die Zahlen umfassen, die sich als Bruch schreiben lassen, umfassen die reellen Zahlen zusätzlich auch noch die Menge der irrationalen Zahlen. Sowohl die rationalen als auch die reellen Zahlen umfassen die Mengen der natürlichen und ganzen Zahlen.
Jede rationale Zahl ist gleichzeitig auch eine reelle Zahl, aber nicht jede reelle Zahl ist auch eine rationale Zahl.

Zahlenräume – Zusammenfassung

Zahlenräume reelle Zahlen

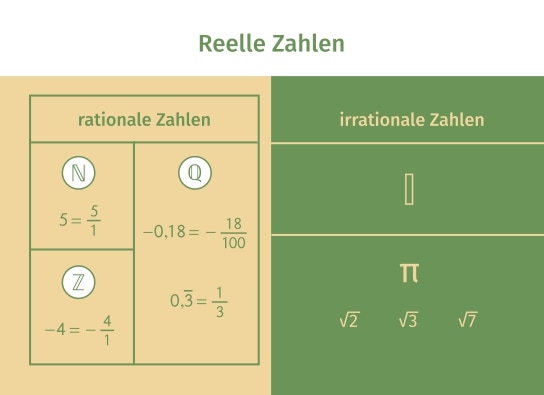
Hier siehst du eine Übersicht der Zahlenräume in der Mathematik. Alle Zahlen, die du kennst, gehören zu den reellen Zahlen. Sie lassen sich in die irrationalen Zahlen \mathbb{I} rechts und die rationalen Zahlen \mathbb{Q} links unterteilen. Zu den rationalen Zahlen gehören auch die ganzen Zahlen \mathbb{Z} mit der Teilmenge der natürlichen Zahlen \mathbb{N}.

Häufig gestellte Fragen zu reellen und irrationalen Zahlen 

Irrationale Zahlen sind Zahlen mit einer unendlichen, sich nicht wiederholenden Anzahl an Nachkommastellen. Ein Beispiel ist die Zahl \pi = 3,\!14159….

Die reellen Zahlen umfassen die Menge der rationalen und der irrationalen Zahlen. So ist beispielsweise die Zahl \pi eine reelle Zahl. Aber auch die Zahlen, 2; -8 und \frac{13}{12} sind reelle Zahlen.

Da die reellen Zahlen die rationalen und irrationalen Zahlen umfassen und beide Mengen auch negative Zahlen umfassen, können reelle Zahlen auch negativ sein, z. B. -\sqrt{2}.

Die Zahl \pi ist eine irrationale Zahl und somit auch eine reelle Zahl.

Da alle Zahlen, die sich als Brüche zweier ganzer Zahlen darstellen lassen, rationale Zahlen sind, sind Brüche ebenfalls reelle Zahlen.

Bei \sqrt{3} handelt es sich um eine irrationale Zahl und somit auch um eine reelle Zahl.

Kommazahlen sind ebenfalls reelle Zahlen. Sind es abbrechende oder periodische Dezimalzahlen, dann handelt es sich um rationale Zahlen. Sind es unendliche, nicht periodische Dezimalzahlen, dann handelt es sich um irrationale Zahlen. Sowohl die Menge der rationalen Zahlen als auch die Menge der irrationalen Zahlen gehören zu den reellen Zahlen.

Das \mathbb{R} steht in Mathe für die Menge der reellen Zahlen.

Leave A Comment

Alle Artikel aus dem Fach Mathematik