Magisches Quadrat – Mathematik
Magische Quadrate sind Quadrate mit Zahlen, bei denen jede Zeile, Spalte und Diagonale die gleiche Summe haben. Erfahre, wie man magische Zahlen berechnet, Quadrate ausfüllt und ihre historische Bedeutung erforscht. Dies und vieles mehr findest du im folgenden Text.
Inhaltsverzeichnis zum Thema Magisches Quadrat
Magisches Quadrat – Erklärung
Ein magisches Quadrat ist ein Quadrat mit der Seitenlänge ![]() . Die Felder des Quadrats sind so mit Zahlen ausgefüllt, dass die Summe jeder Spalte, jeder Zeile und jeder Diagonale genau den gleichen Wert hat. Dieser Wert wird als magische Zahl oder Zauberzahl bezeichnet.
. Die Felder des Quadrats sind so mit Zahlen ausgefüllt, dass die Summe jeder Spalte, jeder Zeile und jeder Diagonale genau den gleichen Wert hat. Dieser Wert wird als magische Zahl oder Zauberzahl bezeichnet.
In den meisten Fällen werden die Zahlen ![]() bis
bis ![]() so eingesetzt, dass sie jeweils einmal vorkommen. Das ist aber nicht bei jedem magischen Quadrat so.
so eingesetzt, dass sie jeweils einmal vorkommen. Das ist aber nicht bei jedem magischen Quadrat so.
Jede Spalte, jede Zeile und jede Diagonale besitzt genau ![]() Felder. Die Gesamtzahl der Felder ist
Felder. Die Gesamtzahl der Felder ist ![]() .
.
Magisches Quadrat ![]()
Ein ![]() magisches Quadrat besitzt insgesamt
magisches Quadrat besitzt insgesamt ![]() Felder. Die Zahlen
Felder. Die Zahlen ![]() bis
bis ![]() müssen so in das Quadrat eingesetzt werden, dass die Summe jeder Spalte, jeder Zeile und jeder Diagonale genau gleich ist. In einem
müssen so in das Quadrat eingesetzt werden, dass die Summe jeder Spalte, jeder Zeile und jeder Diagonale genau gleich ist. In einem ![]() magischen Quadrat mit den Zahlen
magischen Quadrat mit den Zahlen ![]() bis
bis ![]() ist die magische Zahl immer
ist die magische Zahl immer ![]() .
.

Um zu überprüfen, ob das oben stehende Quadrat ein richtig ausgefülltes magisches Quadrat ist, berechnen wir die einzelnen Summen der Spalten, Zeilen und Diagonalen. Beginnend mit den Zeilen:
Zeile: ![]()
Zeile: ![]()
Zeile: ![]()
Nun berechnen wir die Summen der Spalten:
Spalte: ![]()
Spalte: ![]()
Spalte: ![]()
Zuletzt überprüfen wir noch die Summen der Diagonalen:
Diagonale: ![]()
Diagonale: ![]()
Jede Zeile, jede Spalte und jede Diagonale hat die Summe ![]() . Es handelt sich demnach um ein korrekt ausgefülltes
. Es handelt sich demnach um ein korrekt ausgefülltes ![]() magisches Quadrat mit magischer Zahl
magisches Quadrat mit magischer Zahl ![]() .
.
Auch das erste bekannte magische Quadrat war ein ![]() magisches Quadrat mit der magischen Zahl
magisches Quadrat mit der magischen Zahl ![]() . Es geht auf den chinesischen Kaiser Yu zurück, der rund 2200 v. u. Z. lebte.
. Es geht auf den chinesischen Kaiser Yu zurück, der rund 2200 v. u. Z. lebte.
Magische Zahl berechnen
Die magische Zahl lässt sich auch berechnen, wenn die Lösung des magischen Quadrats nicht bekannt ist. Dafür können wir ![]() , also die Anzahl der Zeilen oder Spalten, in die folgende Formel einsetzen:
, also die Anzahl der Zeilen oder Spalten, in die folgende Formel einsetzen:
![]()
Setzen wir zum Beispiel die ![]() für das
für das ![]() magische Quadrat ein, erhalten wir als magische Zahl:
magische Quadrat ein, erhalten wir als magische Zahl:
![]()
Beachte: Diese Formel gilt nur, wenn die Zahlen ![]() bis
bis ![]() in das magische Quadrat eingesetzt werden.
in das magische Quadrat eingesetzt werden.
Magisches Quadrat ausfüllen
Häufig ist ein magisches Quadrat schon teilweise ausgefüllt. Dabei kann es auch vorkommen, dass nicht die Zahlen ![]() bis
bis ![]() eingetragen werden, sondern beliebige andere Zahlen, die auch mehrfach vorkommen können. In solchen Fällen sind die magische Zahl und manchmal auch die Zahlen, die eingetragen werden sollen, vorgegeben.
eingetragen werden, sondern beliebige andere Zahlen, die auch mehrfach vorkommen können. In solchen Fällen sind die magische Zahl und manchmal auch die Zahlen, die eingetragen werden sollen, vorgegeben.
Magisches Quadrat vervollständigen – Rechenweg

Eine Diagonale ist komplett ausgefüllt. Es ergibt sich daraus ![]() als magische Zahl.
als magische Zahl.
In der linken Spalte, der untersten Zeile und der zweiten Diagonale fehlt nur je eine Zahl. Diese Zahlen können ermittelt werden, indem die Summe der anderen beiden in dieser Reihe eingetragenen Zahlen von der magischen Zahl abgezogen wird. Betrachten wir zunächst die linke Spalte. Dort stehen die Zahlen ![]() und
und ![]() . Ziehen wir die Summe der beiden von der
. Ziehen wir die Summe der beiden von der ![]() ab, erhalten wir für die dritte Zahl:
ab, erhalten wir für die dritte Zahl:
![]()
Die ![]() tragen wir nun in das mittlere Kästchen der linken Spalte ein. Genauso gehen wir nun mit der unteren Zeile vor:
tragen wir nun in das mittlere Kästchen der linken Spalte ein. Genauso gehen wir nun mit der unteren Zeile vor:
![]()
Wir erhalten für das mittlere Kästchen der unteren Zeile die Zahl ![]() .
.
Über die beiden Zahlen der Diagonalen erhalten wir für das Kästchen rechts oben die Zahl:
![]()
Für das Kästchen in der Mitte der ersten Zeile ergibt sich die Zahl ![]() und für das Kästchen in der Mitte der rechten Spalte die Zahl
und für das Kästchen in der Mitte der rechten Spalte die Zahl ![]() . Das fertig ausgefüllte magische Quadrat sieht dann so aus:
. Das fertig ausgefüllte magische Quadrat sieht dann so aus:

Beim Lösen eines unvollständig ausgefüllten magischen Quadrats gehst du folgendermaßen vor:
- Magische Zahl bestimmen (wenn keine vorgegeben ist)
- Zeilen und Spalten suchen, in denen nur eine Zahl fehlt
- Alle anderen Zahlen dieser Reihe addieren und Summe von der magischen Zahl abziehen
- Differenz in das leere Kästchen eintragen
- Nächste Zeile oder Spalte mit nur einer fehlenden Zahl suchen
- Solange fehlende Kästchen berechnen, bis das komplette magische Quadrat ausgefüllt ist
Leeres magisches Quadrat – Lösung
Zum Abschluss schauen wir uns an, wie wir selbst ein magisches Quadrat erstellen können.
Je nach Aufbau des magischen Quadrats wird diese Aufgabe auf eine bestimmte Weise gelöst. Mit den folgenden Erklärungen kannst du die Strategien zum Lösen magischer Quadrate lernen. Mit diesen Methoden kannst du das magische Quadrat dann so schnell lösen, dass es einem Zaubertrick gleicht.
Lösung für ungerades ![]()
Ist die Anzahl der Spalten und Zeilen ungerade, dann kannst du die folgende Methode anwenden, um das magische Quadrat auszufüllen. Wir betrachten die Methode wieder am Beispiel des ![]() magischen Quadrats.
magischen Quadrats.
Schritt 1: Wir beginnen mit der kleinsten Zahl, in diesem Fall der ![]() und schreiben sie in das mittlere Feld der ersten Zeile.
und schreiben sie in das mittlere Feld der ersten Zeile.
Schritt 2: Die anderen Zahlen werden in aufsteigender Reihenfolge nach dem folgenden Schema eingesetzt: Vom gerade ausgefüllten Feld gehst du ein Kästchen nach rechts und ein Kasten nach oben und trägst dort die nächste Zahl ein.
Achtung: Landest du dadurch oberhalb der ersten Zeile, dann trägst du die Zahl in die unterste Zeile der gleichen Spalte ein. Landest du außerhalb der rechten Spalte, dann trägst du die Zahl in die ganz linke Spalte in der gleichen Zeile ein. Ist das Kästchen bereits belegt, dann schreibst du die Zahl direkt unterhalb der vorher eingetragenen Zahl.
Lösung für gerades ![]()
Die nächste Methode gilt für magische Quadrate, bei denen ![]() durch
durch ![]() , aber nicht durch
, aber nicht durch ![]() teilbar ist. Das ist zum Beispiel bei einem
teilbar ist. Das ist zum Beispiel bei einem ![]() magischen Quadrat der Fall.
magischen Quadrat der Fall.
Schritt 1: Unterteile das Quadrat in vier gleich große Teilquadrate. Diese haben dann jeweils die Seitenlänge ![]() und
und ![]() Kästchen.
Kästchen.
- Bei einem
 magischen Quadrat haben die Teilquadrate eine Seitenlänge von
magischen Quadrat haben die Teilquadrate eine Seitenlänge von 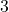 und besitzen jeweils
und besitzen jeweils 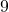 Kästchen.
Kästchen.
Schritt 2: Für jedes Teilquadrat gehst du dann so vor wie bei Quadraten mit einem ungeraden ![]() . Dabei wählst du folgende Zahlen:
. Dabei wählst du folgende Zahlen:
- Quadrat oben links: die ersten
 Zahlen (Beispiel:
Zahlen (Beispiel: 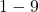 )
) - Quadrat unten rechts: die nächsten
 Zahlen (Beispiel:
Zahlen (Beispiel:  )
) - Quadrat oben rechts: die folgenden
 Zahlen (Beispiel:
Zahlen (Beispiel:  )
) - Quadrat unten links: die letzten
 Zahlen (Beispiel:
Zahlen (Beispiel: 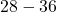 )
)
Beachte: Die Teilquadrate müssen separat betrachtet werden. Landest du außerhalb des Teilquadrats und in einem anderen Teilquadrat, dann gehst du wie bei den oben erklärten Sonderfällen bei Quadraten mit einem ungeraden ![]() vor.
vor.
Schritt 3: Beim Überprüfen der Zeilen und Spalten fällt auf, dass nicht alle die magische Zahl ergeben. Für die endgültige Lösung müssen noch einige Zahlen getauscht werden. Beim Beispiel eines ![]() magischen Quadrats sind das die Zahlen:
magischen Quadrats sind das die Zahlen:
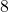 und
und 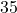
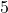 und
und 
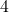 und
und 
Lösung für gerades, durch ![]() teilbares
teilbares ![]()
Ist das ![]() zusätzlich auch durch
zusätzlich auch durch ![]() teilbar, dann wird ein anderer Lösungsweg gewählt. Diesen betrachten wir am Beispiel eines
teilbar, dann wird ein anderer Lösungsweg gewählt. Diesen betrachten wir am Beispiel eines ![]() magischen Quadrats.
magischen Quadrats.
Schritt 1: Zunächst müssen ![]() kleine Quadrate im magischen Quadrat markiert werden. In den Ecken werden jeweils kleine Quadrate mit den Seitenlängen
kleine Quadrate im magischen Quadrat markiert werden. In den Ecken werden jeweils kleine Quadrate mit den Seitenlängen ![]() markiert.
markiert.
- Bei einem
 magischen Quadrat entstehen so vier kleine Quadrate mit einer Seitenlänge von
magischen Quadrat entstehen so vier kleine Quadrate mit einer Seitenlänge von 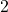 .
.
Zudem wird in der Mitte des magischen Quadrats ein Quadrat mit der Seitenlänge ![]() markiert.
markiert.
- Bei einem
 magischen Quadrat entsteht so ein Quadrat mit der Seitenlänge
magischen Quadrat entsteht so ein Quadrat mit der Seitenlänge 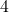 .
.
Schritt 2: Nun zählst du alle Zahlen von ![]() bis
bis ![]() (Beispiel:
(Beispiel: ![]() ) der Reihenfolge nach von oben links beginnend Zeile für Zeile in das magische Quadrat ab. Dabei trägst du die Zahl immer dann in das Kästchen, wenn es im ersten Schritt markiert wurde. Die nicht markierten Kästchen werden zunächst frei gelassen.
) der Reihenfolge nach von oben links beginnend Zeile für Zeile in das magische Quadrat ab. Dabei trägst du die Zahl immer dann in das Kästchen, wenn es im ersten Schritt markiert wurde. Die nicht markierten Kästchen werden zunächst frei gelassen.
- Bei einem
 magischen Quadrat stehen beispielsweise in der ersten Zeile dann ganz links die Zahlen
magischen Quadrat stehen beispielsweise in der ersten Zeile dann ganz links die Zahlen 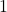 und
und 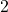 und ganz rechts die Zahlen
und ganz rechts die Zahlen 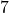 und
und 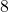 .
.
Schritt 3: Die nicht eingetragenen Zahlen trägst du nun Zeile für Zeile von links nach rechts in die frei gelassenen Kästchen ein. Allerdings in umgekehrter Reihenfolge.
- Die größte nicht eingetragene Zahl bei einem
 magischen Quadrat ist die
magischen Quadrat ist die  . Diese tragen wir in das dritte Kästchen der ersten Zeile ein.
. Diese tragen wir in das dritte Kästchen der ersten Zeile ein.
Schritt 4: Überprüfe jetzt, ob jede Zeile, Spalte und Diagonale die magische Zahl als Summe hat.
- Bei einem
 magischen Quadrat ist die magische Zahl
magischen Quadrat ist die magische Zahl 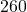 .
.
Häufig gestellte Fragen zum Thema Magisches Quadrat

