Baumdiagramm – Wahrscheinlichkeiten, Pfadregeln und Anwendungen

In der Mathematik werden Baumdiagramme im Bereich der Stochastik verwendet. Sie werden genutzt, um mehrstufige Zufallsversuche zu veranschaulichen.  

Ein Baumdiagramm ist eine grafische Darstellung, die aus einem Startpunkt (Wurzel), Ästen und Knoten besteht. Die Knoten sind dabei in mehreren Stufen angeordnet, die den Stufen des Zufallsversuchs entsprechen. Die Äste verbinden die Knoten der Stufen miteinander. Die Knoten in der letzten Stufe des Baums sind dabei die Endpunkte der Pfade, auf denen der Baum durchlaufen werden kann.

Um ein Baumdiagramm zu zeichnen, muss zunächst geklärt werden, welche Stufen der Baum hat. Wenn wir beispielsweise eine Münze zweimal werfen, dann hat das Baumdiagramm zu diesem zweistufigen Zufallsversuch die folgenden zwei Stufen: 

• Ergebnis des ersten Wurfs
• Ergebnis des zweiten Wurfs

Ausgehend vom Startpunkt haben wir für den ersten Wurf zwei Möglichkeiten: Kopf oder Zahl. Beim zweiten Wurf haben wir in beiden Fällen wieder beide Möglichkeiten, es erfolgt also in der zweiten Stufe jeweils eine weitere Verzweigung mit je zwei Ästen.

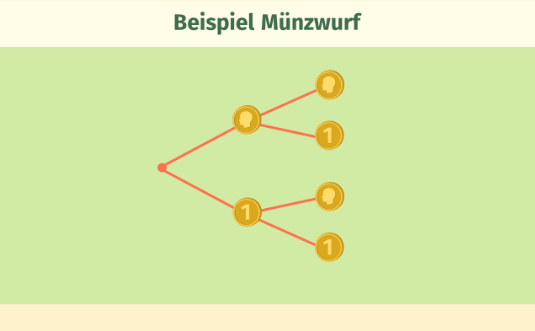
Nach diesem Prinzip kannst du das Baumdiagramm zu jedem mehrstufigen Zufallsversuch Stufe für Stufe aufbauen: Überlege stets, welche Möglichkeiten es im nächsten Schritt des Versuchs gibt.

Die Kombinatorik beschäftigt sich damit, wie viele Möglichkeiten es gibt, verschiedene Dinge zu kombinieren. Dabei kann ein Baumdiagramm zur besseren Vorstellung helfen, da jeder Pfad einem möglichen zusammengesetzten Ergebnis entspricht. Die Anzahl der Möglichkeiten entspricht somit der Anzahl der Pfade, die du in der letzten Stufe des Baumdiagramms abzählen kannst.

Wenn ein Baumdiagramm zur Berechnung von Wahrscheinlichkeiten genutzt wird, ist es hilfreich, die Äste im Baumdiagramm zu beschriften. Dabei wird an jedem Ast die Wahrscheinlichkeit notiert, mit der das Ereignis der nächsten Stufe eintritt. Wir sprechen dann auch von einem Wahrscheinlichkeitsbaum.
Bei dem Baumdiagramm zum zweifachen Münzwurf oben können wir beispielsweise jeden Ast mit der Wahrscheinlichkeit beschriften.

Es gibt zwei Pfadregeln, über die aus einem beschrifteten Baumdiagramm verschiedene Wahrscheinlichkeiten berechnet werden können:

• Produktregel (auch Pfadregel oder 1. Pfadregel)

Die Wahrscheinlichkeit eines Pfads (Elementarereignis) entspricht dem Produkt der Wahrscheinlichkeiten entlang des Pfads.
Zum Beispiel ergibt sich beim zweifachen Münzwurf:

• Summenregel (auch Additionsregel oder 2. Pfadregel)

Die Wahrscheinlichkeit eines (zusammengesetzten) Ereignisses entspricht der Summe der Pfadwahrscheinlichkeiten aller Pfade, die zu diesem Ereignis gehören.
Zum Beispiel ergibt sich beim zweifachen Münzwurf:

Baumdiagramme sind ein praktisches Hilfsmittel bei der Betrachtung von mehrstufigen Zufallsexperimenten und ihren Wahrscheinlichkeiten. Wir betrachten nun noch ein paar typische Beispiele und Fragestellungen zu Baumdiagrammen.

Bei einem mehrstufigen Zufallsexperiment mit Zurücklegen bleibt die Ausgangssituation in jeder Stufe unverändert. Daher ändern sich die Wahrscheinlichkeiten der verschiedenen Äste nicht.

Beim mehrfachen Würfeln entspricht jede Stufe im Baumdiagramm einem Wurf mit den möglichen Ergebnissen , , , , und jeweils mit der Wahrscheinlichkeit . Wird mit mehreren Würfeln gewürfelt, entsprechen die Stufen den Ergebnissen der verschiedenen Würfel, das Baumdiagramm ist identisch. So können beispielsweise mit einem zweistufigen Baumdiagramm alle Wahrscheinlichkeiten für zwei Würfel berechnet werden.

Beim Münzwurf verhält es sich ähnlich wie beim Würfeln. Hier gibt es jedoch auf jeder Stufe nur zwei Möglichkeiten, deren Wahrscheinlichkeit jeweils beträgt.

Auch das Drehen an einem Glücksrad entspricht dem Ziehen mit Zurücklegen, da sich die Aufteilung des Glücksrads in Sektoren über die Drehungen hinweg nicht verändert. Die Anzahl der Verzweigungen und die zugehörigen Wahrscheinlichkeiten hängen von der Ausgestaltung des Rads ab. Die Wahrscheinlichkeit eines Sektors kann über seinen Mittelpunktswinkel mit der Formel ermittelt werden.

Bei einem mehrstufigen Zufallsexperiment ohne Zurücklegen ist die Ausgangssituation in jeder Stufe davon abhängig, was bereits gezogen wurde. Da sich die Zusammensetzung stetig ändert, variieren auch die Wahrscheinlichkeiten an den Ästen des Baumdiagramms.

Das Ziehen aus einer Urne kann mit oder ohne Zurücklegen erfolgen. Werden die gezogenen Objekte nicht wieder zurückgelegt, ändert dies die Zusammensetzung für den nächsten Zug. Hier siehst du ein Beispiel für das Ziehen von Teebeuteln, bei dem sich zu Beginn zwei Beutel Mangotee und drei Beutel Kräutertee in einer Urne befinden. Dies entspricht in der Wahrscheinlichkeitsrechnung einem Baumdiagramm zum Ziehen von Kugeln ohne Zurücklegen.

Hier kannst du mithilfe der Pfadregeln beispielsweise die Wahrscheinlichkeit dafür berechnen, dass du jede Teesorte einmal gezogen hast:

Die Informationen einer Vierfeldertafel können wir auch in einem Baumdiagramm darstellen. Dabei bezieht sich jede Stufe des Baums auf eines der in der Vierfeldertafel betrachteten Ereignisse und . In der ersten Stufe des Baumdiagramms wird zwischen und unterschieden. In der zweiten Stufe erfolgt dann jeweils eine Verzweigung zu und . Die Wahrscheinlichkeiten an den Ästen zur zweiten Stufe sind die bedingten Wahrscheinlichkeiten von und jeweils unter der Bedingung und . Sie können aus den Schnittwahrscheinlichkeiten und den Wahrscheinlichkeiten von und , die der Vierfeldertafel entnommen werden können, berechnet werden. Es entsteht ein zweistufiges Baumdiagramm mit insgesamt vier Pfaden. Dabei tauchen die vier Schnittwahrscheinlichkeiten aus der Vierfeldertafel am Ende der vier Pfade des Baumdiagramms als Pfadwahrscheinlichkeiten auf.

Je nach Fragestellung kann ein Baumdiagramm verkürzt werden. Dazu können nicht relevante Teile ganz weggelassen oder mehrere Ereignisse zusammengefasst werden. Beispielsweise kann es ausreichend sein, beim Würfeln nur die Ergebnisse gerade und ungerade oder und nicht anstelle von , , , , und zu unterscheiden.

Für manche Fragestellungen ist es nötig, ein Baumdiagramm umzukehren. Darunter wird das Vertauschen der ersten und zweiten Stufe eines zweistufigen Baumdiagramms verstanden.

Die Wahrscheinlichkeiten am Ende der Pfade bleiben dabei unverändert. Um die Wahrscheinlichkeiten entlang der Äste zu bestimmen, werden die Pfadregeln benötigt. Damit können zunächst aus dem alten Baum die Wahrscheinlichkeiten für die erste Stufe des umgekehrten Diagramms berechnet werden. Die Wahrscheinlichkeit der zweiten Stufe ergeben sich dann durch ein Umstellen der Formel der Pfadwahrscheinlichkeiten im Baumdiagramm.