Die Scheitelpunktform bei Parabeln – Definition, Erklärung und Beispiele
Die Scheitelpunktform ist eine wichtige Schreibweise für quadratische Funktionen. Sie ermöglicht das direkte Ablesen des Scheitelpunkts einer Parabel. Erfahre, wie die Formeln ineinander umgewandelt werden können und welche Vorteile die Scheitelpunktform bietet. Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Scheitelpunktform
Die Scheitelpunktform einer quadratischen Funktion einfach erklärt
Eine quadratische Funktion ist eine ganzrationale Funktion vom Grad ![]() , das heißt, der höchste Exponent der Variable
, das heißt, der höchste Exponent der Variable ![]() , der in der Funktionsgleichung auftaucht, ist
, der in der Funktionsgleichung auftaucht, ist ![]() . In der allgemeinen Form hat eine quadratische Funktion die Form
. In der allgemeinen Form hat eine quadratische Funktion die Form
![]() ,
, ![]() .
.
Wenn ![]() ist, wird auch von der Normalform gesprochen.
ist, wird auch von der Normalform gesprochen.
Die Scheitelpunktform ist eine andere Darstellungsform für die Funktionsgleichung einer quadratischen Funktion, die durch Termumformungen aus der allgemeinen Form entstehen kann bzw. in die allgemeine Form umgewandelt werden kann. Sie lautet:
![]()
Der Scheitelpunkt einer quadratischen Funktion
Der Graph einer quadratischen Funktion beschreibt eine Parabel. Der Scheitelpunkt einer nach oben (nach unten) geöffneten Parabel ist ihr tiefster (höchster) Punkt. Die Koordinaten des Scheitelpunkts einer Parabel lassen sich direkt aus der Scheitelpunktform bestimmen, daher kommt auch ihr Name:
![]()
Andersherum lässt sich aus einem gegebenen Scheitelpunkt auch die zugehörige Funktionsgleichung bestimmen, indem die Koordinaten des Scheitelpunkts in die Formel der Scheitelpunktform eingesetzt werden. Der Streck- oder Stauchfaktor ![]() muss zusätzlich bestimmt werden.
muss zusätzlich bestimmt werden.
Der Scheitelpunkt ist nicht nur der höchste (tiefste) Punkt einer Parabel, durch ihn verläuft auch die Symmetrieachse.
Beispiele:
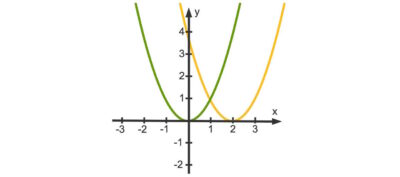
- Die Normalparabel mit der Funktionsgleichung
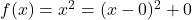 hat den Scheitelpunkt
hat den Scheitelpunkt  .
. - Die Funktion
 mit
mit 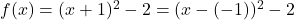 hat den Scheitelpunkt
hat den Scheitelpunkt  .
.

Scheitelpunktform und allgemeine Form ineinander umwandeln
Mit Termumformungen lassen sich die verschiedenen Formen der Funktionsgleichung einer quadratischen Funktion ineinander umformen.
Von der Scheitelpunktform zur allgemeinen Form
Bei der Umformung von der Scheitelform in die allgemeine Form muss die Klammer mithilfe der binomischen Formel aufgelöst und dann die Terme zusammengefasst werden.
Dies schauen wir uns am Beispiel der Funktion ![]() an:
an:

Von der allgemeinen Form zur Scheitelpunktform
Für die Umformung von der allgemeinen Form in die Scheitelpunktform wird im Grunde rückwärts vorgegangen: Mithilfe der quadratischen Ergänzung wird der Term so umgeformt, dass eine binomische Formel angewendet werden kann.
Auch dies schauen wir uns an zwei Beispielen an, zunächst beginnen wir mit einer Funktion, die in Normalform vorliegt, und bringen diese in Scheitelpunktform.

Im zweiten Beispiel möchten wir die Scheitelpunktform zu der Funktion ![]() aufstellen. Hier ist der Koeffizient vor
aufstellen. Hier ist der Koeffizient vor ![]() nicht
nicht ![]() und wir müssen diesen deswegen zuerst ausklammern:
und wir müssen diesen deswegen zuerst ausklammern:

Vorteile der Scheitelpunktform
Aus der Scheitelpunktform können nicht nur Koordinaten des Scheitelpunkts berechnet werden, es lassen sich auch anhand der Parameter ![]() ,
, ![]() und
und ![]() Eigenschaften des Verlaufs der Parabel erkennen.
Eigenschaften des Verlaufs der Parabel erkennen.
In der Tabelle sind Eigenschaften der Funktion mit der Gleichung ![]() zusammengefasst. Bei den Beispielen ist der grüne Funktionsgraph jeweils der Graph der Normalparabel
zusammengefasst. Bei den Beispielen ist der grüne Funktionsgraph jeweils der Graph der Normalparabel ![]() mit Scheitelpunkt
mit Scheitelpunkt ![]() .
.
| Parameter | Eigenschaften | Beispiel |
|---|---|---|
| Streckfaktor |
|
Die rote Parabel hat den Funktionsterm
|
|
Die gelbe Parabel hat den Funktionsterm
|
|
|
Die blaue Parabel hat den Funktionsterm
|
Beispiel
Wir schauen uns nun noch ein Beispiel an, in dem die verschiedenen Eigenschaften kombiniert sind. Wir betrachten die quadratische Funktion ![]() , die in Scheitelpunktform vorliegt:
, die in Scheitelpunktform vorliegt: ![]()
Da ![]() ,
, ![]() und
und ![]() , ist der Graph gegenüber der Normalparabel um
, ist der Graph gegenüber der Normalparabel um ![]() Einheit nach rechts und um
Einheit nach rechts und um ![]() Einheiten nach oben verschoben, es liegt keine Streckung oder Stauchung vor, die Öffnung ist genau wie bei der Normalparabel. Der Scheitelpunkt liegt bei
Einheiten nach oben verschoben, es liegt keine Streckung oder Stauchung vor, die Öffnung ist genau wie bei der Normalparabel. Der Scheitelpunkt liegt bei ![]() . Der Graph der Funktion
. Der Graph der Funktion ![]() ist im folgenden Bild in Blau eingezeichnet, die Normalparabel in Grün.
ist im folgenden Bild in Blau eingezeichnet, die Normalparabel in Grün.

Häufig gestellte Fragen zum Thema Scheitelpunktform