Beweise durch vollständige Induktion – Erklärung, Beispiele und Tipps
Lerne, wie man mit vollständiger Induktion mathematische Aussagen für alle natürlichen Zahlen beweist. Die vier Schritte – Induktionsanfang, -annahme, -schritt und -schluss – sind entscheidend. Möchtest du mehr über vollständige Induktion und Beispiele erfahren?
Inhaltsverzeichnis zum Thema Vollständige Induktion
Vollständige Induktion einfach erklärt
Die vollständige Induktion ist eine Beweismethode in der Mathematik. Damit können Aussagen bewiesen werden, die für die Menge der natürlichen Zahlen gelten. Formal schreibt man:
![]() gilt für alle
gilt für alle ![]() .
.
Die vier Schritte der vollständigen Induktion
Bewiesen werden soll die Aussage ![]() für alle
für alle ![]() .
.
- Induktionsanfang: Die Aussage wird für eine beliebige Zahl, in der Regel für
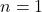 bzw. die kleinste Zahl, für die die Aussage gelten soll, bewiesen.
bzw. die kleinste Zahl, für die die Aussage gelten soll, bewiesen. - Induktionsannahme (oder Induktionsvoraussetzung): Es wird angenommen, dass
 für ein
für ein  gilt.
gilt. - Induktionsschritt: Nun wird gezeigt, dass die Aussage
 auch für den Nachfolger von
auch für den Nachfolger von 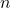 gilt, also dass
gilt, also dass  richtig ist.
richtig ist.
In diesem Schritt ist in der Regel am meisten zu tun: Mit mehr oder weniger aufwendigen Umformungen und Argumentationen wird die Aussage gezeigt. Dabei wird die Induktionsannahme verwendet, also dass
gezeigt. Dabei wird die Induktionsannahme verwendet, also dass  bereits gilt.
bereits gilt. - Induktionsschluss: Nun wird aus 1. bis 3. gefolgert, dass
 für alle
für alle  gilt.
gilt.
Beispielaufgaben mit der vollständigen Induktion lösen
Im Folgenden schauen wir uns Aufgaben an, in denen Aussagen mit vollständiger Induktion bewiesen werden können.
Gaußsche Summenformel mit vollständiger Induktion
Wir möchten nun die Summenformel von Gauß beweisen. Diese lautet wie folgt:
![]() :
:  gilt für alle
gilt für alle ![]() .
.
Das bedeutet, dass die Summe aller Zahlen von ![]() bis zu einer beliebigen Zahl
bis zu einer beliebigen Zahl ![]() mit der Formel
mit der Formel ![]() berechnet werden kann.
berechnet werden kann.
1. Induktionsanfang
Wir zeigen, dass die Formel für ![]() gilt:
gilt:

Die Aussage ![]() stimmt also.
stimmt also.
2. Induktionsannahme
Da die Aussage ![]() für
für ![]() gilt, ist anzunehmen, dass die Aussage
gilt, ist anzunehmen, dass die Aussage ![]() für ein beliebiges
für ein beliebiges ![]() gilt.
gilt.
3. Induktionsschritt
Nun zeigen wir, dass unter der Voraussetzung, dass ![]() gilt, auch
gilt, auch ![]() gilt. Es muss also gezeigt werden, dass gilt:
gilt. Es muss also gezeigt werden, dass gilt:
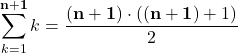
Es gilt:

Für die weitere Umformung können wir nun unsere Induktionsannahme verwenden, da wir ja schon wissen, dass
 gilt.
gilt.
Damit erhalten wir folgenden Ausdruck, den wir weiter umformen:
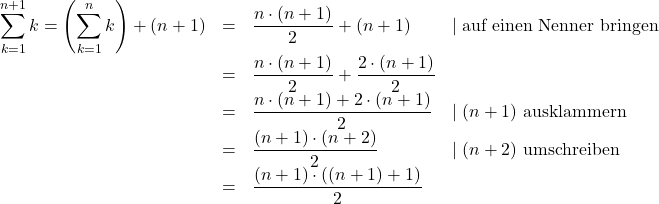
4. Induktionsschluss
In der letzten Zeile der Umformungsschritte steht nun genau, was gezeigt werden sollte, also die Aussage ![]() :
:

Damit haben wir gezeigt, dass ![]() für alle
für alle ![]() gilt.
gilt.
Bernoullische Ungleichung mit vollständiger Induktion
Die bernoullische Ungleichung besagt, dass für jede natürliche Zahl ![]() und jede reelle Zahl
und jede reelle Zahl ![]() folgende Ungleichung gilt:
folgende Ungleichung gilt:
![]() :
: ![]()
1. Induktionsanfang
Wir zeigen, dass die Formel für ![]() gilt:
gilt:
![]() :
: ![]()
2. Induktionsannahme
Da die Aussage ![]() für
für ![]() gilt, ist anzunehmen, dass die Aussage
gilt, ist anzunehmen, dass die Aussage ![]() für ein beliebiges
für ein beliebiges ![]() gilt, also:
gilt, also:
![]() :
: ![]()
3. Induktionsschritt
Nun zeigen wir, dass unter der Voraussetzung, dass ![]() gilt, auch
gilt, auch ![]() gilt. Es muss also gezeigt werden, dass gilt:
gilt. Es muss also gezeigt werden, dass gilt:
![]() :
: ![]()
Wir formen um und verwenden dabei die Induktionsannahme:

4. Induktionsschluss
In der letzten Zeile der Umformungsschritte steht nun genau, was gezeigt werden sollte.
![]() :
: ![]()
Damit haben wir gezeigt, dass gilt:
![]() für alle
für alle ![]()
Häufig gestellte Fragen zum Thema Vollständige Induktion

