Kegel berechnen – einfach erklärt

Lerne, was Kegel sind: geometrische Körper mit kreisförmiger Grundfläche und Spitze. Entdecke die Unterschiede zwischen geraden und schiefen Kegeln sowie die Berechnung von Höhe, Mantelfläche und Volumen. Interessiert? Dies und vieles mehr findest du im folgenden Text!

Inhaltsverzeichnis zum Thema Kegel berechnen

Die Berechnung von Kegeln im Überblick

  • Kegel sind geometrische Körper, die eine kreisförmige Grundfläche aufweisen, deren Randpunkte alle mit der Spitze des Kegels verbunden sind.

  • Ein Kegel hat eine Ecke, zwei Flächen und eine Kante. 

  • Für einen Kegel mit Grundkreisradius r, Höhe h und Mantellinie m gilt:

    Oberfläche O = \pi \cdot r \cdot (r + m)

    Volumen V = \dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h

Kegel berechnen: Lernvideo

Quelle: sofatutor.com

Kegel – Definition und Merkmale

Ein Kegel ist ein geometrischer Körper. Körper sind immer dreidimensional. Ein Kegel besitzt eine kreisförmige Grundfläche, weshalb er auch als Kreiskegel bezeichnet wird. Jeder Randpunkt des Kreises ist mit der Spitze des Kegels verbunden. 

Ein Kegel hat somit:

  • eine Ecke – die sogenannte Spitze,
  • zwei Flächen – die Grundfläche und die Mantelfläche,
  • eine Kante – den Rand der Grundfläche.

Darin liegt auch der entscheidende Unterschied zur Pyramide. Diese besitzt mindestens vier Ecken, vier Flächen und sechs Kanten. Das liegt daran, dass die Grundfläche einer Pyramide ein beliebiges Vieleck (Dreieck, Viereck, Fünfeck …) ist. 

Arten von Kegeln

Wir unterscheiden zwei verschiedene Arten von Kegeln. Die geraden und die schiefen Kegel.

Gerader Kegel

gerader Kegel

Quelle sofatutor.com

In der Grafik siehst du einen geraden Kegel, dabei ist:

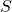  • S: die Spitze 
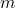  • m: die Mantellinie
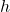  • h: die Höhe des Kegels
  • r: der Radius der Grundfläche

Bei einem geraden Kegel befindet sich die Spitze S genau über dem Mittelpunkt der Grundfläche. Zudem ist die Mantellinie m an allen Stellen gleich lang. Die Höhe ist bei einem geraden Kegel der Abstand zwischen dem Mittelpunkt der Grundfläche und der Spitze. 

Hinweis: Manchmal wird die Mantellinie auch mit dem Buchstaben s bezeichnet. 

Schiefer Kegel

Die folgende Grafik zeigt einen schiefen Kegel:

schiefer Kegel

Die Spitze liegt bei schiefen Kegeln nicht direkt über dem Mittelpunkt der Grundfläche. Zudem ist die Mantellinie nicht an allen Stellen gleich lang. In der Grafik ist erkennbar, dass die Mantellinie links deutlich länger ist als rechts. Als Höhe wird der Abstand zwischen der Ebene, in der die Grundfläche liegt, und der Spitze bezeichnet. Die Spitze muss sich dabei nicht über der Grundfläche befinden.

Kegel berechnen – Formeln und Beispiele

Wir betrachten im Folgenden die Formeln zur Berechnung von wichtigen Größen wie Mantellinie, Oberfläche und Volumen von Kegeln. 

Hinweis: Die Formeln und Beispiele beziehen sich auf gerade Kreiskegel, bei schiefen Kreiskegeln ist die Berechnung der Oberfläche deutlich komplizierter, da die Mantellinie keine einheitliche Länge hat. Für das Volumen gilt dagegen für alle Kegel die gleiche Formel.

Kegel – Höhe und Mantellinie berechnen

Der Abstand zwischen der Grundfläche und der Spitze eines geraden Kegels wird als Höhe h bezeichnet und lässt sich mit der folgenden Formel berechnen:

h = \sqrt{m^2 - r^2}

Dabei ist:

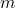  • m: die Mantellinie
  • r: der Radius der Grundfläche

Daraus ergibt sich für die Berechnung der Mantellinie die Formel:

m = \sqrt{h^2 + r^2}

Beispiel

m = 10~\text{cm}

r = 6~\text{cm}

h = \sqrt{m^2 - r^2} = \sqrt{(10~\text{cm})^2 - (6~\text{cm})^2} = 8~\text{cm}

Kegel – Grundfläche berechnen

Da die Grundfläche A_G eines Kegels ein Kreis ist, lässt sich der Flächeninhalt der Grundfläche mit der folgenden Formel berechnen:

A_G = \pi \cdot r^2

Dabei ist:

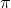  • \pi: die Kreiszahl mit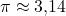 \pi \approx 3,\!14
  • r: der Radius der Grundfläche

Beispiel

r = 6~\text{cm}

A_G = \pi \cdot r^2 = \pi \cdot (6~\text{cm})^2 \approx 113,\!1~\text{cm}^2

Kegel – Mantelfläche berechnen

Wird die Mantelfläche an der Mantellinie aufgeschnitten, ergibt sich ein Kreissektor. Das ist in der folgenden Grafik erkennbar:

Mantelfläche Kegel

Die Mantellinie m bildet dabei den Radius dieses Kreissektors. Die Fläche dieses Kreissektors ist die Mantelfläche M. Diese lässt sich mit der folgenden Formel berechnen:

M = \pi \cdot r \cdot m

Dabei ist:

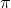  • \pi: die Kreiszahl 
  • r: der Radius der Grundfläche
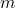  • m: die Mantellinie

Beispiel

m = 10~\text{cm}

r = 6~\text{cm}

M = \pi \cdot r \cdot m = \pi \cdot 6~\text{cm} \cdot 10~\text{cm} \approx 188,\!5~\text{cm}^2

Kegel – Oberfläche berechnen

Die Gesamtoberfläche O setzt sich zusammen aus der Grundfläche A_G und der Mantelfläche M:

O = A_G + M = \pi \cdot r^2 + \pi \cdot r \cdot m = \pi \cdot r \cdot (r + m)

Dabei ist:

  • A_G: die Grundfläche
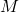  • M: die Mantelfläche
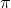  • \pi: die Kreiszahl 
  • r: der Radius der Grundfläche
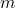  • m: die Mantellinie

Beispiel

m = 10~\text{cm}

r = 6~\text{cm}

O = \pi \cdot r \cdot (r + m) = \pi \cdot 6~\text{cm} \cdot (6~\text{cm} + 10~\text{cm}) \approx 301,\!6~\text{cm}^2

Auf das gleiche Ergebnis kommst du auch, wenn du die Grundfläche und die Mantelfläche addierst:

O = A_G + M = 113,\!1~\text{cm}^2 + 188,\!5~\text{cm}^2 = 301,\!6~\text{cm}^2

Kegel – Volumen berechnen

Um das Volumen (den Rauminhalt) eines Kegels zu berechnen, nutzen wir die Formel: 

V = \dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h

Dabei ist:

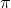  • \pi: die Kreiszahl 
  • r: der Radius der Grundfläche
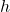  • h: die Höhe des Kegels

Beispiel

r = 6~\text{cm}

h = 8~\text{cm}

V = \dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h = \dfrac{1}{3} \cdot \pi \cdot (6~\text{cm})^2 \cdot 8~\text{cm} = 301,\!6~\text{cm}^3

Kegel – Öffnungswinkel berechnen

Der Winkel zwischen der Mantellinie und der Linie, die die Höhe angibt, wird als halber Öffnungswinkel bezeichnet. Je größer der Öffnungswinkel, desto breiter ist der Kegel.
Für den halben Öffnungswinkel \varphi gilt:

\sin \varphi = \dfrac{r}{m} ~ \Rightarrow ~ \varphi = \arcsin \dfrac{r}{m}

\cos \varphi = \dfrac{h}{m} ~ \Rightarrow ~ \varphi = \arccos \dfrac{h}{m}

\tan \varphi = \dfrac{r}{h} ~ \Rightarrow ~ \varphi = \arctan \dfrac{r}{h}

Für den Öffnungswinkel \alpha gilt dann: \alpha = 2 \cdot \varphi

Beispiel

m = 10~\text{cm}

r = 6~\text{cm}

\varphi = \arcsin \dfrac{r}{m} = \arcsin \dfrac{6~\text{cm}}{10~\text{cm}} \approx 36,\!9^\circ

\Righarrow ~ \alpha = 2 \cdot \varphi = 2 \cdot 36\!,9^\circ = 73,\!8^\circ

Kegelformeln auf einen Blick

In der folgenden Tabelle sind noch einmal die wichtigsten Formeln zusammengefasst. Dabei bezeichnet r den Radius der Grundfläche.

Formel
Höhe h h = \sqrt{m^2 - r^2}
Mantellinie m m = \sqrt{h^2 + r^2}
Grundfläche A_G A_G = \pi \cdot r^2
Mantelfläche M M = \pi \cdot r \cdot m
Oberfläche O O = A_G + M = \pi \cdot r \cdot (r + m)
Volumen V V = \dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h

Kegel – Oberfläche Rechner



Kegel – Volumen Rechner



Kegel – Schrägbild

Anhand eines Beispiels schauen wir uns an, wie wir ein Schrägbild eines Kegels zeichnen. Gegeben sind der Durchmesser d der Grundfläche und die Höhe h.

d = 6~\text{cm}

h = 4~\text{cm}

Da es sich um ein Schrägbild handelt, wird die Grundfläche als Ellipse gezeichnet. Zunächst zeichnen wir dafür den Durchmesser als waagerechte Linie mit dem Mittelpunkt der Grundfläche in der Mitte ein. Durch den Mittelpunkt zeichnen wir einen weiteren Durchmesser im Verzerrungswinkel des Schrägbilds, der um den Verzerrungsfaktor verkürzt ist. Die Enden aller vier Linien werden nun zu einer Ellipse verbunden. Der hintere Teil der Ellipse ist von der Mantelfläche verdeckt, weshalb wir ihn nur gestrichelt zeichnen. 

Schrägbild Kegel

Die Spitze des Kegels liegt genau über dem Schnittpunkt der beiden Linien. Wir tragen die Höhe also genau senkrecht von diesem Schnittpunkt aus ab. Die Spitze verbinden wir im Anschluss mit den Endpunkten des Durchmessers.

Kegelstumpf – Definition und Berechnungen

Wird ein kleiner Teil des Kegels unterhalb der Spitze parallel zur Grundfläche abgeschnitten, entsteht ein Kegelstumpf.

Kegelstumpf

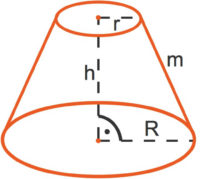
Die Grundfläche des Kegelstumpfs hat den Radius R. Zusätzlich besitzt der Kegelstumpf eine Deckfläche mit dem Radius r mit r < R. 

In der folgenden Tabelle sind die Formeln zur Berechnung der Grundfläche, der Deckfläche, der Mantelfläche, der Oberfläche und des Volumens eines Kegelstumpfs aufgelistet.

Formel
Grundfläche A_G A_G = \pi \cdot R^2
Deckfläche A_D A_D = \pi \cdot r^2
Mantelfläche M M = \pi \cdot m \cdot (R + r)
Oberfläche O O = A_G + A_D + M = \pi \cdot R^2 + \pi \cdot r^2 + \pi \cdot m \cdot (R + r) = \pi \cdot (R^2 + r^2 + m \cdot (R + r))
Volumen V V = \dfrac{1}{3} \cdot \pi \cdot h \cdot (R^2 + R \cdot r + r^2)

Dabei ist:

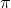  • \pi: die Kreiszahl
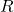  • R: der Radius der Grundfläche
  • r: der Radius der Deckfläche
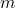  • m: die Mantellinie
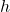  • h: die Höhe

Kegel berechnen – Aufgaben

Aufgabe 1: Radius des Kegels berechnen

Gegeben sind das Volumen V und die Höhe h eines Kegels. Berechne den Radius der Grundfläche!

Im Anschluss kannst du aus dem Radius auch den Durchmesser des Kegels berechnen.

V = 75,\!4~\text{cm}^3

h = 4,\!5~\text{cm}

Lösung Aufgabe 1

Um den Radius zu erhalten, stellen wir die Formel für das Volumen nach r um und setzen die beiden gegebenen Größen ein:

V = \dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h

r = \sqrt{\dfrac{3 \cdot V}{\pi \cdot h}} = \sqrt{\dfrac{3 \cdot 75,\!4~\text{cm}^3}{\pi \cdot 4,\!5~\text{cm}}} \approx 4~\text{cm}

Der Radius der Grundfläche beträgt 4~\text{cm}. 

Um den Durchmesser d zu berechnen, multiplizieren wir den Radius mit 2 und erhalten:

d = 2 \cdot r = 2 \cdot 4~\text{cm} = 8~\text{cm}

Aufgabe 2: Grundfläche, Mantelfläche und Oberfläche berechnen

Von einem Kegel sind der Radius r der Grundfläche und die Mantellinie m gegeben. Berechne mithilfe dieser Größen die Grundfläche, die Mantelfläche und die Oberfläche des Kegels.

r = 2~\text{cm}

m = 5~\text{cm}

Lösung Aufgabe 2

Um die Grundfläche A_G und die Mantelfläche M zu berechnen, setzen wir die gegebenen Größen in die jeweiligen Formeln ein und erhalten:

A_G = \pi \cdot r^2 = \pi \cdot (2~\text{cm})^2 \approx 12,\!6~\text{cm}^2

M = \pi \cdot r \cdot m = \pi \cdot 2~\text{cm} \cdot 5~\text{cm} \approx 31,\!4~\text{cm}^2

Die Oberfläche ist die Summe der Grundfläche und der Mantelfläche und beträgt:

O = A_G + M = 12,\!6~\text{cm}^2 + 31,\!4~\text{cm}^2 = 44~\text{cm}^2

Die Grundfläche des Kegels beträgt 12,\!6~\text{cm}^2, die Mantelfläche des Kegels beträgt 31,\!4~\text{cm}^2 und die Oberfläche des Kegels beträgt 44~\text{cm}^2.

Kegel – Beispiele aus dem Alltag

Auch im Alltag begegnen uns Kegel regelmäßig. So haben Schultüten bei Schuleinführungen häufig die Form eines Kegels, genauso wie Eiswaffeln. Auch spitze Hüte von Hexen und Zauberern haben in vielen Fällen eine Kegelform.

Häufig gestellte Fragen zum Thema Kegel berechnen

Kegel sind geometrische Körper mit einer kreisförmigen Grundfläche. Alle Randpunkte der Grundfläche sind mit der Spitze verbunden.

Ein Kegel ist daran erkennbar, dass er eine kreisförmige Grundfläche und eine Spitze besitzt. Die Spitze kann sich direkt mittig über der Grundfläche (gerader Kegel) oder versetzt dazu (schiefer Kegel) befinden.

Ein Kegel hat zwei Flächen, die Grundfläche und die Mantelfläche.

Ein Kegel hat eine Ecke, die sogenannte Spitze.

Ein Kegelstumpf ist ein Kegel ohne Spitze. Er besitzt stattdessen parallel zur Grundfläche eine Deckfläche.

Pyramiden besitzen deutlich mehr Ecken, Kanten und Flächen als Kegel, da ihre Grundfläche ein beliebiges Vieleck ist. Kegel hingegen haben eine kreisförmige Grundfläche.

Es gibt gerade und schiefe Kegel.

Da Kegel eine kreisförmige Grundfläche haben, werden sie auch als Kreiskegel bezeichnet.

Um die Grundfläche eines Kegels zu berechnen, nutzen wir die Formel A_G = \pi \cdot r^2. Die Mantelfläche lässt sich mit der Formel M = \pi \cdot r \cdot m berechnen. Die Oberfläche ist die Summe aus Grundfläche und Mantelfläche. Das Volumen berechnen wir mit der Formel V = \dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h.

Den Öffnungswinkel \alpha berechnen wir über den halben Öffnungswinkel \varphi, wobei \alpha = 2 \cdot \varphi. Der halbe Öffnungswinkel berechnet sich als: \varphi = \arcsin \dfrac{r}{m}.

Als M wird die Mantelfläche eines Kegels bezeichnet. 

Schultüten bei Schuleinführungen, Eiswaffeln und Hüte von Hexen und Zauberern sind Beispiele für Kegel im Alltag.

Leave A Comment

Alle Artikel aus dem Fach Mathematik