Geradenschar – Definition, Erklärung und Anwendung
Eine Geradenschar beinhaltet unendlich viele Geraden, die durch einen zusätzlichen Parameter, den Scharparameter, bestimmt werden. Lerne, wie man parallel verlaufende oder sich in einem Punkt schneidende Geradenschar errichtet und löse typische Aufgaben. Interessiert? Dies und vieles mehr erwarten dich im folgenden Text!
Inhaltsverzeichnis zum Thema Geradenschar
Das Quiz zum Thema: Geradenschar
Was beschreibt eine Geradenschar?
Frage 1 von 5
Was ist ein Geradenbüschel?
Frage 2 von 5
Wie kann eine Geradenschar in der Ebene beschrieben werden?
Frage 3 von 5
Was ist die Besonderheit einer parallelen Geradenschar?
Frage 4 von 5
Wie kann der Büschelpunkt einer Geradenschar bestimmt werden?
Frage 5 von 5
Geradenscharen im Überblick
- Eine Geradenschar enthält einen Scharparameter
in der Geradengleichung. Das Einsetzen eines beliebigen Werts für
in die Gleichung einer Geradenschar liefert die Gleichung einer Geraden der Schar.- Eine Geradenschar, bei der sich alle Geraden in einem Punkt schneiden, heißt Geradenbüschel.
Quelle: sofatutor.com
Wie willst du heute lernen?
Geradenschar – Definition
Eine Geradengleichung, die zusätzlich zur Variablen einen weiteren Parameter enthält, beschreibt unendlich viele Geraden, die als Geradenschar bezeichnet werden. Der zusätzliche Parameter wird auch Scharparameter genannt.
Geradenschar – Arten und Gleichung
Eine Geradenschar kann in der Ebene durch eine lineare Funktionen 
oder im Raum durch eine Parametergleichung 
beschrieben werden. Abhängig davon, wo in der Geradengleichung ein Scharparameter steht, kann die Geradenschar verschiedene Formen annehmen.
Parallele Geradenschar
Eine Schar paralleler Geraden entsteht, wenn alle Geraden die gleiche Richtung haben. In der Ebene ist dies der Fall, wenn die Steigung 
durch den Scharparameter nicht verändert wird. Im Raum haben die Geraden der Schar die gleiche Richtung, wenn der Richtungsvektor 
unabhängig vom Wert des Scharparameters ist.
Hier siehst du einige Geraden einer parallelen Geradenschar in einem dreidimensionalen Koordinatensystem dargestellt. Jede Gerade der Schar hat denselben Richtungsvektor .
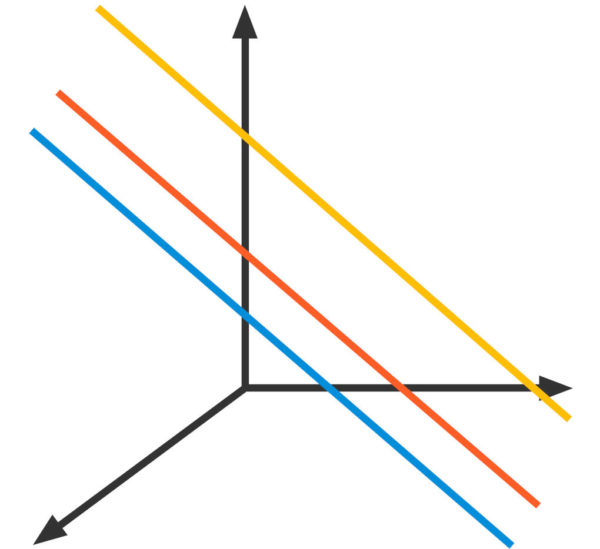
Quelle sofatutor.com
Geradenbüschel
Als Geradenbüschel wird eine Geradenschar bezeichnet, deren Geraden alle durch einen gemeinsamen Punkt verlaufen. Dieser wird dann Büschelpunkt der Geradenschar genannt. Dies ist in der Ebene zum Beispiel der Fall, wenn der Scharparameter nur die Steigung verändert. Im Raum hat eine Geradenschar einen Büschelpunkt, wenn beispielsweise der Scharparameter nur den Richtungsvektor der Geraden verändert.
Hier siehst du einige Geraden eines Geradenbüschels in einem dreidimensionalen Koordinatensystem dargestellt. Jede Gerade der Schar geht durch den Punkt 
.
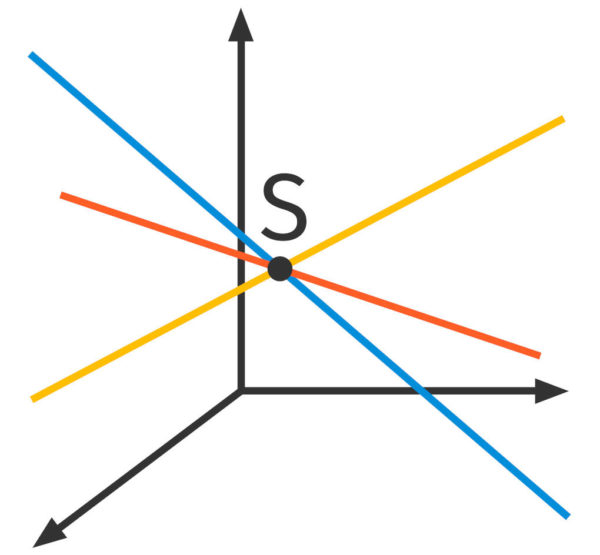
Geradenschar – Eigenschaften
Es gibt verschiedene Eigenschaften, die auf eine Geradenschar als Ganzes (für einen beliebigen Wert von ) oder auf einzelne Geraden einer Schar (für bestimmte Werte von ) zutreffen können.
Geradenschar in der Ebene
Eine Geradenschar in der Ebene wird durch eine lineare Funktionsgleichung beschrieben. Der Scharparameter kann in der Steigung , im 
-Achsenabschnitt 
oder in beiden vorkommen.
Geradenschar – Nullstellen und Schnittpunkte
Die Nullstelle einer Geradenschar, ihr Schnittpunkt mit der -Achse oder Schnittpunkte mit anderen Funktionen können mit der Funktionsgleichung wie bei einer Geraden bestimmt werden.
Enthält das Ergebnis dabei den Scharparameter , dann kann der passende Wert für jede Gerade der Schar durch Einsetzen berechnet werden. Enthält das Ergebnis den Scharparameter nicht, ist der Punkt für alle Geraden der Schar gleich.
Geradenschar – Steigung
Die Steigung einer Geradenschar kann direkt aus der Funktionsgleichung abgelesen werden, sie entspricht dem Faktor vor der Variable 
.
Ist die Steigung einer Geradenschar unabhängig vom Scharparameter , dann verlaufen alle Geraden der Schar parallel zueinander.
Geradenschar mit Vektoren
Eine Geradenschar im Raum wird durch eine Parametergleichung beschrieben. Dabei ist 
der Stützvektor und der Richtungsvektor der Geradenschar. Sie können beide einen Scharparameter in beliebigen Einträgen enthalten.
Geradenschar – Spurpunkte
Die Schnittpunkte einer Geradenschar mit den Koordinatenebenen, die sogenannten Spurpunkte, können wie gewohnt berechnet werden.
Enthält das Ergebnis dabei den Scharparameter , dann können die passenden Punkte für jede Gerade der Schar durch Einsetzen bestimmt werden. Enthält das Ergebnis den Scharparameter nicht, sind die Punkte für alle Geraden der Schar gleich.
Geradenschar – Lagebeziehungen
Auch bei der Bestimmung der Lagebeziehungen kann bei einer Geradenschar so vorgegangen werden wie sonst bei Geraden. Bei Ergebnissen, die den Scharparameter enthalten, wird das Ergebnis für eine bestimmte Gerade der Schar durch Einsetzen von ermittelt. Außerdem kann der passende Wert für so bestimmt werden, dass die Schargerade bestimmte Eigenschaften aufweist.
Geradenschar – Anwendung
Im Folgenden betrachten wir zwei typische Anwendungen von Geradenscharen in Aufgaben.
Geradenschar mit Parametern aufstellen
Wir wollen die Gleichung einer Geradenschar aufstellen, die folgende Eigenschaften erfüllt:
- Die Geradenschar verläuft parallel zur Ebene
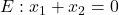. - Alle Geraden der Schar gehen durch den Punkt
.
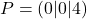Eine Geradengleichung besteht aus einem Stützvektor und einem Richtungsvektor . Damit alle Geraden durch den Punkt 
verlaufen, wählen wir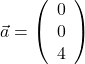 
.
Wir lesen den Normalenvektor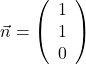 
aus der Ebenengleichung von 
ab. Damit die Geradenschar 
parallel zu verläuft, muss für den Richtungsvektor gelten:
Wir setzen ein:
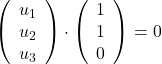
Daraus erhalten wir:
Wir wählen 
. Für die 
-Koordinate des Vektors können wie den Scharparameter einsetzen, da diese beliebig ist.
Damit ergibt sich:
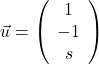
Die Gleichung der Geradenschar mit den gewünschten Eigenschaften lautet:
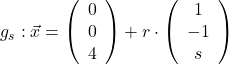
Gerade aus einer Schar ermitteln
Wir wollen nun aus der Geradenschar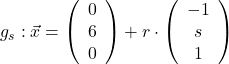 
diejenige Gerade ermitteln, die den Schnittpunkt 
mit der 
-Ebene hat.
Dies bedeutet, dass wir einen Wert für den Scharparameter suchen, für den die folgende Gleichung eine Lösung hat:
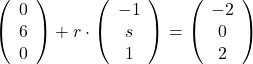
Aus der letzten Zeile der Gleichung erhalten wir:
Wir setzen diesen Wert in die zweite Zeile ein und erhalten:
Damit ist die gesuchte Gerade:
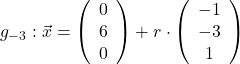
Die Geradenschar schneidet die -Ebene im Punkt , wenn der Parameter den Wert 
annimmt.
Häufig gestellte Fragen zum Thema Geradenscharen
Eine Geradenschar wird durch eine Geradengleichung beschrieben, die einen zusätzlichen Parameter, den sogenannten Scharparameter, enthält. Für jeden Wert dieses Parameters ergibt sich eine Gerade der Schar.
Eine Geradenschar besteht aus unendlich vielen Geraden. Diese können alle durch einen Punkt, den sogenannten Büschelpunkt, gehen oder parallel zueinander verlaufen.
Eine Gerade liegt in einer Ebene, wenn alle Punkte der Geraden auch Punkte der Ebene sind. Rechnerisch nachweisen lässt sich dies, wenn Gerade und Ebene parallel verlaufen und ein Punkt der Geraden in der Ebene liegt.
Als Büschelpunkt wird der gemeinsame Schnittpunkt aller Geraden einer Geradenschar bezeichnet. Eine solche Geradenschar wird auch Geradenbüschel genannt.
Der Büschelpunkt kann als Schnittpunkt zweier bestimmter Geraden der Geradenschar bestimmt werden, dabei gehst du folgendermaßen vor:
- Bestimme zwei unterschiedliche Geradengleichungen durch Einsetzen von zwei verschiedenen Werten für den Scharparameter.
- Bestimme den Schnittpunkt der Geraden durch Gleichsetzen.
- Setze den Schnittpunkt in die allgemeine Gleichung der Geradenschar ein, um zu überprüfen, ob tatsächlich alle Geraden der Schar durch diesen Punkt verlaufen.
Es gibt Geradenscharen in der Ebene, d. h. in Form von Funktionen, und im Raum, d. h. in vektorieller Form. Beide können aus parallelen Geraden bestehen oder ein Geradenbüschel bilden.
Wenn alle Geraden einer Schar in einer Ebene liegen, dann kann diese Ebene folgendermaßen aus der Geradenschar bestimmt werden:
- Bestimme zwei unterschiedliche Geradengleichungen durch Einsetzen von zwei verschiedenen Werten für den Scharparameter.
- Bestimme die Gleichung der Ebene
, die beide Geraden enthält. - Überprüfe, ob jede Schargerade in liegt.
Alle Artikel aus dem Fach Mathematik