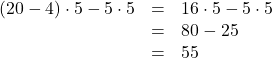Was ist ein Term? – Erklärung, Definition und Beispiele zum Thema Terme

Terme sind sinnvolle Rechenausdrücke, die sich aus Zahlen, Variablen, Rechenzeichen und Klammern zusammensetzen. Je nachdem ob Variablen in einem Term vorkommen, unterscheiden wir zwischen Termen mit und ohne Variablen.

Terme ohne Variablen bestehen aus

• Zahlen,
• Klammern,
• Rechen- und Vorzeichen.

Du kannst sie mithilfe von Rechenregeln berechnen.

Einzelne Zahlausdrücke wie zum Beispiel oder sind Terme bestehend aus einer Zahl.
Verbindest du diese beiden Zahlen mit einem , erhältst du den Term .
Ein Term mit Klammern wäre zum Beispiel .

Terme mit Variablen enthalten neben Zahlen, Klammern und Rechenzeichen zusätzlich Variablen.
Ein Term mit Variable wäre zum Beispiel .
Dieser Term besteht aus zwei Termen: der Variable und dem Zahlterm , die durch das Rechenzeichen zu einer Addition verknüpft sind.
Es können auch mehrere Variablen in einem Term vorkommen. Dann ist es häufig sinnvoll, den Term umzuformen, indem du gleichartige Terme zusammenfasst. Dabei können dir das Kommutativ- und das Assoziativgesetz helfen.

Terme heißen gleichwertig, wenn sie durch ein Gleichheitszeichen verbunden werden können. Du kannst auch sagen, die beiden Terme sind äquivalent. Das ist der Fall, wenn beide Terme für jeden möglichen Wert der Variablen den gleichen Termwert besitzen.

Betrachte die Gleichung .
Setzt du beispielhaft ein paar Werte für die Variable ein, erhältst du auf beiden Seiten
stets das gleiche Ergebnis.

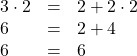
Auch Terme ohne Variablen können äquivalent sein. In diesem Fall vereinfachst und
berechnest du auf beiden Seiten des Gleichheitszeichens und vergleichst anschließend, ob
die Werte der Terme übereinstimmen.
Beachte dabei wie im folgenden Beispiel die Rechenregel „Punkt vor Strich“.

Terme sind mehr als nur Rechnungen. Alltagsbeispiele können durch sie gelöst und berechnet werden. Das gilt sowohl für Terme mit als auch ohne Variablen.

Insbesondere bei Textaufgaben in Mathe ist es oft hilfreich, wenn du Terme aufstellen und vereinfachen kannst.
Ein Beispiel ist der zu zahlende Preis, wenn du dir ein Eis kaufen möchtest und eine Kugel € kostet. Dann kannst du den Preis berechnen, indem du den Preis pro Kugel Eis mal die Anzahl der Kugeln nimmst. Der Preis wird also beschrieben durch den Term , sodass du die Gleichung erhältst.
Der Preis für Kugeln Eis wäre entsprechend €.

Um Terme berechnen zu können, musst du diese so weit wie möglich vereinfachen.
Liegt dir ein Term ohne Variablen vor, kannst du dich an die folgenden Schritte halten.
1. Klammern berechnen
2. Punktrechnung (Multiplikation und Division)
3. Strichrechnung (Addition und Subtraktion)

Wir wenden diese Schritte auf beiden Seiten einer Gleichung an:

So sehen wir, dass die Terme tatsächlich äquivalent sind.

Terme können auch Wurzeln und Potenzen enthalten. Möchtest du Terme mit Wurzeln und Potenzen vereinfachen, ist es wichtig, dass du dich an die entsprechenden Wurzel- und Potenzgesetze hältst. Potenzen berechnest du nach den Klammern und vor den Punktrechnungen. Das restliche Vorgehen entspricht der oben aufgeführten Schrittfolge.

Besitzt der Term, den du berechnen möchtest, nicht nur Zahlen, sondern auch Variablen, ist ein anderes Vorgehen nötig, da du für die Variablen keine konkreten Werte angegeben hast.

1. Ausmultiplizieren der Klammern (Distributivgesetz)
2. Umstellen (Kommutativgesetz)
3. Zusammenfassen

Betrachte das folgende Beispiel.

Wende zunächst das Distributivgesetz an, um die Klammern aufzulösen. Durch die Multiplikation kannst du die Terme anschließend vereinfachen.

Ein Umstellen mithilfe des Kommutativgesetzes ist in diesem Fall nicht nötig, da die gleichartigen Terme bereits nebeneinanderstehen und du diese so zusammenfassen kannst.

Anschließend berechnest du den Term so weit wie möglich unter Beachtung der Punkt-vor-Strich-Regel.

Sieh dir die folgenden Beispiele an, um ein Gefühl für das Vorgehen beim Terme vereinfachen zu bekommen.

Beispiel 1:
Du hast den Term gegeben. Vereinfache ihn so weit wie möglich.

Vereinfache den Term zunächst, indem du die Klammer mithilfe des Distributivgesetzes ausmultiplizierst und anschließend Multiplikation und Addition berechnest.

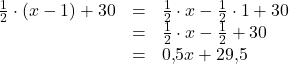
Eine weitere Vereinfachung ist nicht möglich, da nur gleichnamige Terme zusammengefasst werden können.

Beispiel 2:
Gestern warst du mit deinen Eltern im Zoo. Dort habt ihr viele Tiere gesehen. Unter anderem gab es ein Gehege, in dem Elefanten, Giraffen und Strauße zusammen gehalten wurden. Gib einen Term für die Anzahl der Beine an, die alle Tiere im Gehege zusammen haben.

• Die 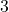Elefanten haben je 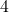Beine: .
• Die 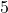Giraffen haben ebenfalls je 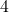Beine: .
• Jeder der 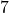Strauße hat 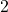Beine: .

Insgesamt haben alle Tiere im Gehege demnach
Beine.

Wir können nach diesem Prinzip auch allgemein einen Term für die Anzahl der Beine in einem Gehege mit Elefanten, Giraffen und Straußen angeben: