Sinussatz und Cosinussatz – Erklärung

Der Sinussatz und der Cosinussatz sind wichtige Sätze der Trigonometrie, mit denen die Seiten und Winkel von Dreiecken berechnet werden können. Für die Formeln wird immer die folgende Beschriftung von Dreiecken als Grundlage verwendet:

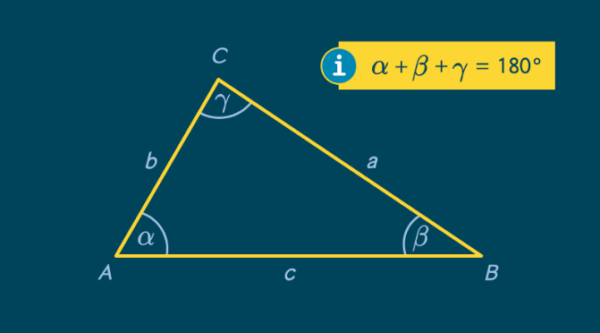
Dabei sind , und die drei Seiten des Dreiecks. Gegenüber von liegt der Winkel , gegenüber von liegt der Winkel und gegenüber von liegt der Winkel .
Zudem gilt in Dreiecken der Innenwinkelsatz. Dieser besagt, dass die Summe der drei Innenwinkel immer beträgt.

Achtung: Der Sinussatz und der Cosinussatz dürfen nicht mit dem Sinus und dem Cosinus verwechselt werden. Bei dem Sinus und dem Cosinus handelt es sich um Funktionen, die sogenannten trigonometrischen Funktionen. Sinus und Cosinus kommen aber in den Sätzen vor und sind namensgebend dafür.

Der Sinussatz beschreibt das Verhältnis zwischen der Seite eines beliebigen Dreiecks und dem gegenüberliegenden Winkel. Die Formel des Sinussatzes lautet:

Sind von zwei Winkeln und den gegenüberliegenden Seiten drei Größen bekannt, kann die vierte Größe mit dem Sinussatz berechnet werden.
Der Sinussatz gilt für alle beliebigen Dreiecke, also sowohl für rechtwinklige als auch für nicht rechtwinklige Dreiecke. Sogar für stumpfwinklige Dreiecke ist der Sinussatz gültig.

Mit dem Sinussatz können sowohl Seiten als auch Winkel berechnet werden. Dafür muss die Ausgangsformel entsprechend umgeformt werden. Schauen wir uns das an zwei Beispielen genauer an.

Beispiel 1: Seite mit dem Sinussatz berechnen

Gegeben ist das folgende Dreieck:

Es soll die Seite berechnet werden.
Da für den Winkel die gegenüberliegende Seite gegeben ist, nutzen wir die Formel:

Um die gesuchte Seite zu berechnen, müssen wir den Sinussatz so umformen, dass allein steht:

Nun können wir die gegebenen Größen einsetzen und erhalten für die Seite die Länge:

Beispiel 2: Winkel mit dem Sinussatz berechnen

Gegeben ist das folgende Dreieck:

Es soll der Winkel berechnet werden.
Da sowohl die Seite als auch der Winkel nicht bekannt sind, wählen wir die Formel:

Zunächst stellen wir diese Formel nach der gesuchten Größe, also dem Winkel , um:

Um nicht nur den Sinus des Winkels, sondern den Winkel zu berechnen, wenden wir die Umkehrfunktion des Sinus an, , die auf dem Taschenrechner mit abgekürzt wird:

Setzen wir die gegebenen Werte in die Formel ein, erhalten wir für :

Löse die folgenden Aufgaben mit dem Sinussatz.

Aufgabe 1: Sinussatz umstellen

In einem allgemeinen Dreieck sind die folgenden Größen gegeben:

Bestimme den fehlenden Winkel .
Berechne die fehlenden Seiten und .

Lösung Aufgabe 1a

Durch den Innenwinkelsatz wissen wir, dass gilt. Somit berechnet sich als:

Lösung Aufgabe 1b
Nach dem Sinussatz gilt:

Daraus ergibt sich für die Seite :

Und für die Seite :

Aufgabe 2: Sinussatz beim rechtwinkligen Dreieck

Für ein rechtwinkliges Dreieck sind die folgenden drei Größen gegeben:

Berechne die fehlenden Winkel und .
Berechne die fehlende Seite .

Lösung Aufgabe 2a

Nach dem Sinussatz gilt:

Daraus folgt für den Winkel :

Da ein rechter Winkel ist, gilt . Daraus folgt für :

Den Winkel können wir über den Innenwinkelsatz berechnen.

Lösung Aufgabe 2b

Nach dem Sinussatz gilt:

Daraus ergibt sich für die Seite :

Es kann vorkommen, dass es beim Sinussatz keine eindeutige Lösung gibt. Das ist dann der Fall, wenn zwei Seiten und der Winkel, der der kürzeren Seite gegenüberliegt, gegeben sind. In diesem Fall gibt es drei Möglichkeiten:

1. keine Lösung: Der Sinuswert des zu berechnenden Winkels ist größer als .
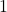2. genau eine Lösung: Der Sinuswert des zu berechnenden Winkels ist genau 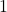, das bedeutet, der Winkel ist .
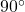3. zwei Lösungen: Ein Wert wird vom Taschenrechner berechnet, der andere ergibt sich, wenn der berechnete Wert von 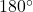abgezogen wird.

Beispiel

Der Sinuswert von ist größer als , weshalb diese Aufgabe keine Lösung besitzt.

Der Cosinussatz (auch Kosinussatz) beschreibt das Verhältnis zwischen den drei Seiten eines beliebigen Dreiecks und einem Winkel. Auch der Cosinussatz gilt für alle Dreiecke.
Die Formeln für den Cosinussatz lauten:

Beachte: Die dritte Seite eines Dreiecks können wir nur dann mit dem Cosinussatz berechnen, wenn die beiden gegebenen Seiten den gegebenen Winkel einschließen.

Cosinussatz im rechtwinkligen Dreieck
Ein besonderer Fall des Cosinussatzes ist der Satz des Pythagoras. Er gilt nur für rechtwinklige Dreiecke und lautet:

Dabei muss die Hypothenuse (also die längste Seite) des Dreiecks sein. Der letzte Term der entsprechenden Formel des Cosinussatzes fällt weg, da ist und somit gilt:

Mit dem Cosinussatz können sowohl Seiten als auch Winkel berechnet werden. Schauen wir uns das an zwei Beispielen genauer an.

Beispiel 1: Seite eines allgemeinen Dreiecks mit dem Cosinussatz berechnen

Von einem allgemeinen Dreieck sind die folgenden drei Größen gegeben:

Gesucht ist die Seite . Nach dem Cosinussatz gilt für :

Setzen wir die Werte ein, erhalten wir für :

Beispiel 2: Winkel mit dem Cosinussatz berechnen – Cosinussatz umstellen

Sind alle drei Seiten gegeben, können mithilfe des Cosinussatzes auch Winkel berechnet werden. Dafür muss die Formel entsprechend umgestellt werden.

Gegeben sind die drei Seiten:

Gesucht ist der Winkel . Um diesen zu berechnen, muss der Cosinussatz nach umgestellt werden:

Nun können wir die gegebenen Werte in die Formel einsetzen und erhalten für :

Die folgenden Größen eines allgemeinen Dreiecks sind gegeben:

Aufgabe:

Berechne die fehlende Seite mithilfe des Cosinussatzes.
Berechne die Winkel und .

Lösung Aufgabe 1a

Nach dem Cosinussatz gilt:

Daraus folgt für die Seite :

Lösung Aufgabe 1b

Nach dem Cosinussatz gilt:

Daraus folgt für :

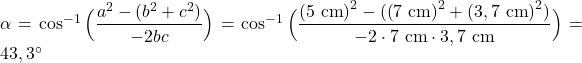
Den Winkel können wir nun über den Innenwinkelsatz berechnen: