Assoziativgesetz – Erklärung, Formel und Beispiele
Erfahre, wie das Assoziativgesetz besagt, dass bei mehrfacher Addition oder Multiplikation Klammern beliebig gesetzt oder weggelassen werden können, ohne das Ergebnis zu ändern. Außerdem: Unterschiede zu anderen Rechengesetzen.
Inhaltsverzeichnis zum Thema Assoziativgesetz
Was regelt das Assoziativgesetz bei der Addition und Multiplikation?
Frage 1 von 5
Was besagt das Assoziativgesetz bei der Addition?
Frage 2 von 5
Wie lautet das Assoziativgesetz bei der Multiplikation?
Frage 3 von 5
Gilt das Assoziativgesetz auch bei der Subtraktion und Division?
Frage 4 von 5
Was ist der Unterschied zwischen dem Assoziativgesetz und dem Kommutativgesetz?
Frage 5 von 5
Was ist das Assoziativgesetz?
Das Assoziativgesetz ist ein wichtiges Rechengesetz in der Mathematik. Im Folgenden wird das Assoziativgesetz einfach erklärt.
Assoziativgesetz Merksatz: Bei mehrfacher Addition oder Multiplikation können Klammern beliebig gesetzt oder weggelassen werden.
Mehrfache Addition und Multiplikation bedeutet, dass mehrere Zahlen entweder addiert oder multipliziert werden. Wichtig ist, dass nur eine Rechenart in der Aufgabe vorkommt, ansonsten gilt das Gesetz nicht. Betrachten wir die folgenden Beispiele:
![]()
Das gleiche Ergebnis erhalten wir, wenn wir die Klammer anders setzen:
![]()
Auch wenn wir die Rechnung ganz ohne Klammern durchführen, ändert sich nichts am Ergebnis:
![]()
Für die Multiplikation sehen wir am folgenden Beispiel, dass die Klammersetzung das Ergebnis nicht verändert:
![]()
![]()
![]()
Der Name Assoziativgesetz hat wie viele mathematische Begriffe einen lateinischen Ursprung. Er stammt vom lateinischen Wort associare ab, das mit vereinigen, verbinden, verknüpfen oder vernetzen übersetzt werden kann. Aus diesem Grund wird das Gesetz auch manchmal Verknüpfungsgesetz oder Verbindungsgesetz genannt.
Wie lautet das Assoziativgesetz bei der Addition?
Das Assoziativgesetz sagt aus, dass das Umsetzen oder Weglassen von Klammern bei mehrfacher Addition keinen Einfluss auf das Ergebnis hat. Durch Umsetzen oder Weglassen von Klammern ändert sich zwar die Reihenfolge der Rechenschritte, nicht aber das Ergebnis. Allgemein können wir schreiben:
![]()
Assoziativgesetz Addition – Beispiele
Auf einen formalen Beweis für das Assoziativgesetz wollen wir hier verzichten. Stattdessen schauen wir uns noch einmal ein Beispiel an und gehen es gemeinsam durch.
Betrachten wir die folgende Aufgabe:
![]()
Berechnen wir zunächst die erste Summe. Wir addieren zuerst in der Klammer und erhalten:
![]()
Das gleiche Ergebnis erhalten wir, wenn wir zuerst ![]() rechnen und dann die
rechnen und dann die ![]() addieren.
addieren.
![]()
Es spielt also keine Rolle, welche der drei Zahlen wir zuerst addieren, das Ergebnis ist immer gleich.
Man sagt: Die Addition ist assoziativ.
Wie lautet das Assoziativgesetz bei der Multiplikation?
Auch für die Multiplikation besagt das Assoziativgesetz, dass das Umsetzen oder Weglassen von Klammern bei mehrfacher Multiplikation keinen Einfluss auf das Ergebnis hat. Allgemein können wir für die Multiplikation schreiben:
![]()
Assoziativgesetz Multiplikation – Beispiel
Betrachten wir noch einmal ein Beispiel und gehen es gemeinsam durch.
![]()
Berechnen wir zunächst das erste Produkt. Wir multiplizieren zuerst in der Klammer und erhalten:
![]()
Das gleiche Ergebnis erhalten wir, wenn wir zuerst ![]() rechnen und das dann mit
rechnen und das dann mit ![]() multiplizieren.
multiplizieren.
![]()
Es spielt also keine Rolle, welche der drei Zahlen wir zuerst multiplizieren, das Ergebnis ist immer gleich.
Man sagt: Die Multiplikation ist assoziativ.
Gilt das Assoziativgesetz auch bei Subtraktion und Division?
Für die Subtraktion und Division gilt das Assoziativgesetz nicht. Dort wird durch das Verändern der Klammersetzung auch das Ergebnis verändert. Das lässt sich an den folgenden Beispielen zeigen:
Beispiel 1:
![]()
![]()
Die beiden Ergebnisse stimmen nicht überein.
Beispiel 2:
![]()
![]()
Auch hier stimmen die beiden Ergebnisse nicht überein. Daraus können wir folgern, dass Subtraktion und Division nicht assoziativ sind.
Das Assoziativgesetz gilt ebenfalls dann nicht, wenn verschiedene Rechenarten in einer Aufgabe verwendet werden. Auch wenn es sich bei den Rechenarten um Addition und Multiplikation handelt, wird in diesem Fall das Ergebnis verändert. Das lässt sich am folgenden Beispiel zeigen:
![]()
![]()
Die Ergebnisse stimmen nicht überein, da bei dieser Aufgabe sowohl Addition als auch Multiplikation verwendet wurden. Das bedeutet: Das Assoziativgesetz gilt nicht.
Was ist der Unterschied zwischen dem Kommutativgesetz und dem Assoziativgesetz?
Beide Gesetze gelten für die Addition und die Multiplikation. Das Assoziativgesetz bezieht sich jedoch auf die Klammersetzung, während sich das Kommutativgesetz auf die Reihenfolge der Summanden oder Faktoren bezieht.
Genaueres über das Kommutativgesetz erfährst du im Text über das Kommutativgesetz.
Eselsbrücke für das Assoziativgesetz
Der Begriff Assoziativgesetz lässt sich am Anfang nicht so leicht merken. Aus diesem Grund gibt es eine Eselsbrücke, die helfen soll, diesen lateinischen Begriff immer im Kopf zu behalten. Aus den ersten fünf Buchstaben kannst du dir eine Wortgruppe herleiten, die auch gleich auf die Aussage des Gesetzes schließen lässt:
As–so–z-iativgesetz → Anders soll’s zusammen!
Mit dieser Aussage kannst du dir den Namen Assoziativgesetz leichter merken.
Assoziativgesetz – Anwendungen
Allgemein gilt das Assoziativgesetz dann, wenn das Weglassen oder Verschieben von Klammern keinen Einfluss auf das Ergebnis hat. Ein paar Anwendungen des Gesetzes wollen wir hier kurz betrachten.
Assoziativgesetz bei Brüchen
Das Assoziativgesetz gilt auch bei der Addition oder Multiplikation von Brüchen. Es kann hier das Zusammenfassen oder Kürzen von Brüchen erleichtern.
Beispiel:
![]()
Bei dieser Rechnung hast du verschiedene Möglichkeiten, Klammern zu setzen. Die erste Möglichkeit ist es, die Klammer um die ersten beiden Brüche zu setzen, um diese zuerst zu addieren.
![]()
Zunächst musst du die beiden Brüche in der Klammer erweitern, um sie zu addieren. Im Anschluss kannst du den dritten Bruch direkt addieren. Somit kannst du dir die Addition dieser drei Brüche mit der Klammersetzung erleichtern.
Die zweite Möglichkeit, die Klammern zu setzen, ist folgende:
![]()
Wie du siehst, ist diese Klammersetzung jedoch weniger vorteilhaft, da sie mehr Rechenschritte benötigt, um zum Ergebnis zu kommen.
Assoziativgesetz bei Vektoren
Bei der Addition von Vektoren dürfen die Klammern beliebig gesetzt werden. Die Addition von Vektoren ist also assoziativ.
Beispiel:
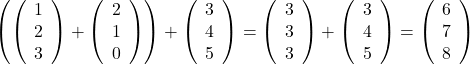
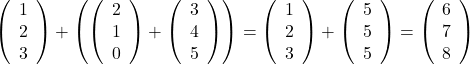
Für das Skalarprodukt gilt das Assoziativgesetz nicht, da das Skalarprodukt nur mit zwei Vektoren gebildet werden kann.
Assoziativgesetz in der Mengenlehre
Das Assoziativgesetz gilt für Schnitt und Vereinigung von Mengen.
![]()
![]()
Beispiel:
![]()
![]()
![]()
Bilden wir zuerst den Schnitt von ![]() und
und ![]() , erhalten wir:
, erhalten wir:
![]()
Nun bilden wir die Schnittmenge des Ergebnisses mit ![]() und erhalten die Menge:
und erhalten die Menge:
![]()
Schauen wir uns nun an, was die Schnittmenge von ![]() und
und ![]() ist:
ist:
![]()
Bilden wir nun die Schnittmenge des Ergebnisses mit ![]() , erhalten wir die Menge:
, erhalten wir die Menge:
![]()
Egal welche Schnittmenge wir zuerst bilden, die Schnittmenge aller drei Mengen ist immer gleich. Wir sagen auch: Der Schnitt von Mengen ist assoziativ.
Häufig gestellte Fragen zum Thema Assoziativgesetz

