Symmetrie – erklärt für die Grundschule
Erfahre, was Symmetrie in der Mathematik bedeutet, einschließlich Achsensymmetrie und Drehsymmetrie. Entdecke, wie man symmetrische Figuren erkennen und zeichnen kann. Symmetrie im Alltag und in der Natur wird ebenfalls beleuchtet. Mehr dazu im folgenden Text!
Inhaltsverzeichnis zum Thema Symmetrie
Wie willst du heute lernen?
Symmetrie Definition
Symmetrie ist eine Eigenschaft von geometrischen Objekten, also Figuren oder Körpern. Eine Figur ist symmetrisch, wenn sie durch eine Bewegung auf sich selbst abgebildet werden kann. Diese Bewegung kann zum Beispiel eine Spiegelung oder Drehung sein. Aus diesen Bewegungen ergeben sich zwei verschiedene Symmetriearten, die im Folgenden genauer erklärt werden.
Achsensymmetrie einfach erklärt
Wenn eine Figur durch Spiegelung an einer Achse auf sich selbst abgebildet werden kann, ist sie achsensymmetrisch.
Alle achsensymmetrischen Figuren haben eine Symmetrieachse. Die Symmetrieachse teilt die Figur in zwei genau gleich große Teile, die genau aufeinanderpassen. Figuren können mehr als eine Symmetrieachse haben.
Im folgenden Bild siehst du Beispiele der Achsensymmetrie.

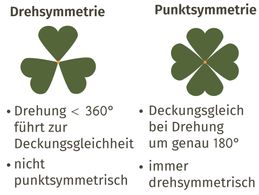
Drehsymmetrie einfach erklärt
Wenn eine Figur durch Drehung um einen Punkt auf sich selbst abgebildet werden kann, ist sie drehsymmetrisch. Drehsymmetrische Figuren haben einen Drehpunkt, der auch Zentrum genannt wird.

Im folgenden Bild siehst du ein Beispiel der Drehsymmetrie.

Der Punkt stellt das Zentrum dar. Um diesen Punkt herum kannst du die Sonne drehen, bis sie auf sich selbst abgebildet wird.
Eine besondere Art der Drehsymmetrie ist die Punktsymmetrie. Eine Figur ist punktsymmetrisch, wenn sie durch eine Drehung um 180![]() (halbe Drehung) auf sich selbst abgebildet wird.
(halbe Drehung) auf sich selbst abgebildet wird.
Symmetrie und Asymmetrie
Asymmetrie ist das Gegenteil von Symmetrie. Eine Figur ist asymmetrisch, wenn sie seitenungleich ist.
Das Verkehrsschild im Bild ist beispielsweise asymmetrisch. Du kannst keine Symmetrieachse einzeichnen, da die linke und die rechte Seite von dieser Achse immer unterschiedlich aussehen.

Symmetrie bestimmen
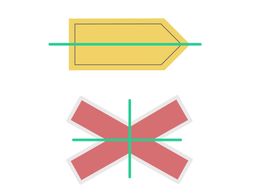
Kannst du bei der folgenden Figur erkennen, welche Art der Symmetrie vorliegt?

Die Figur ist achsensymmetrisch, weil das Schild zwei Symmetrieachsen hat.
Außerdem ist die Figur drehsymmetrisch, weil sie durch eine halbe Drehung um das Zentrum auf sich selbst abgebildet werden kann.

Symmetrie überprüfen
Um eine Figur auf Achsensymmetrie zu überprüfen, kannst du an der Symmetrieachse einen Spiegel anlegen. Die Symmetrieachse kannst du auch Spiegelachse nennen. Die zweite Hälfte der Figur siehst du nun durch den Spiegel. Wenn sie genauso aussieht wie die echte zweite Hälfte, ist die Figur achsensymmetrisch.
Symmetrische Figuren herstellen und zeichnen
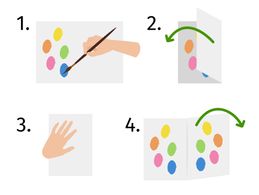
Kennst du Klecksbilder? Das sind immer Bilder mit einer Achsensymmetrie.
Indem du das Papier zu Beginn in der Mitte faltest, erstellst du die Symmetrieachse. Nun malst du Kleckse auf eine Seite. Wenn du das Blatt Papier nun zusammenklappst und anschließend wieder öffnest, hast du ein achsensymmetrisches Bild hergestellt.
Achsensymmetrische Figuren kannst du auch zeichnen.
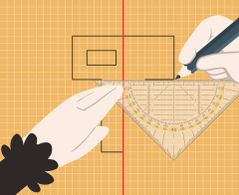
Auf Karopapier kannst du achsensymmetrische Figuren gut ergänzen. Dabei musst du darauf achten, dass die Linien der Figur auf beiden Seiten dieselbe Länge und alle Punkte den gleichen Abstand zur Symmetrieachse haben.
Um zu überprüfen, ob du richtig gezeichnet hast, kannst du einen Spiegel an der Symmetrieachse anlegen. Wenn die zweite Hälfte durch den Spiegel exakt so aussieht, wie du sie gezeichnet hast, ist deine Zeichnung korrekt.
Symmetrie im Alltag und der Umwelt
Im Alltag kannst du viele symmetrische Figuren entdecken.
Auf dem Weg zur Schule gibt es bei dir sicher auch Verkehrsschilder. Diese sind oft symmetrisch.
Auch Häuser sind meist symmetrisch gebaut. Wir Menschen gestalten viele Dinge in unserer Umwelt symmetrisch, weil wir die Symmetrie als schön und ordentlich empfinden.
Oftmals hat die Symmetrie aber auch einen praktischen Nutzen. Schmetterlinge und Flugzeuge sind beispielsweise beinahe achsensymmetrisch.

Das ist auch wichtig, denn nur so können sie richtig fliegen.
Symmetrische Formen
Manche geometrische Formen sind symmetrisch.
Das Quadrat hat vier Symmetrieachsen.
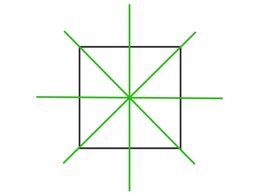
Außerdem ist es drehsymmetrisch. Das Zentrum befindet sich in der Mitte des Quadrats. Nach jeweils einer Vierteldrehung wird das Quadrat wieder auf sich selbst abgebildet.
Auch das Rechteck ist achsensymmetrisch. Weißt du, wie viele Symmetrieachsen es hat?

Rechtecke, die keine Quadrate sind, haben insgesamt zwei Symmetrieachsen.

Außerdem ist es drehsymmetrisch. Das Zentrum befindet sich in der Mitte des Rechtecks, dort, wo sich die Symmetrieachsen schneiden. Nach jeweils einer halben Drehung wird das Rechteck wieder auf sich selbst abgebildet.
Es gibt auch symmetrische Dreiecke.
Gleichschenklige Dreiecke sind Dreiecke mit zwei gleich langen Seiten. Sie haben immer eine Symmetrieachse.

Gleichseitige Dreiecke sind Dreiecke mit drei gleich langen Seiten. Sie haben immer drei Symmetrieachsen und sind drehsymmetrisch.

Häufig gestellte Fragen zum Thema Symmetrie









Alle Artikel aus dem Fach Mathematik