Brüche dividieren – Definition, Erklärung und Beispiele

Erfahre, wie man Brüche divisioniert, indem man den Kehrwert des zweiten Bruchs bildet und beide multipliziert. Zusätzliche Themen umfassen Kürzen vor der Division und das Beachten von Vorzeichen. Interessiert? Lies weiter für detaillierte Erklärungen und Beispiele!

Inhaltsverzeichnis zum Thema Brüche dividieren

Das Quiz zum Thema: Brüche dividieren

Wie wird die Division von zwei Brüchen definiert?

Frage 1 von 5

Was bedeutet der Kehrwert eines Bruchs?

Frage 2 von 5

Warum ist es wichtig, den Kehrwert des zweiten Bruchs zu bilden?

Frage 3 von 5

Wie wirkt sich das Vorzeichen bei der Division von Brüchen aus?

Frage 4 von 5

Wann ist es sinnvoll, Brüche vor der Division zu kürzen?

Frage 5 von 5

Brüche dividieren im Überblick

  • Bei der Division zweier Brüche gibt der Quotient an, wie häufig der Divisor (zweiter Bruch) in den Dividenden (erster Bruch) passt.
  • Um zwei Brüche miteinander oder besser gesagt durcheinander zu dividieren, müssen ein paar wichtige Schritte beachtet werden.
  • Wenn durch einen Bruch dividiert wird, muss zunächst der Kehrwert des Bruchs gebildet werden.
  • Die Multiplikation mit dem Kehrwert entspricht der Division durch einen Bruch.
Brüche dividieren

Quelle sofatutor.com

Wie werden zwei Brüche dividiert? – Erklärung

Brüche geben Anteile an und bestehen aus drei Teilen: zwei Zahlen und einem Bruchstrich. Die Zahl, die über dem Bruchstrich steht, nennen wir Zähler. Die Zahl unter dem Bruchstrich heißt Nenner. Division von Brüchen bedeutet, dass der Dividend oder der Divisor oder beide Brüche sind. Das Dividieren von Brüchen wird im Folgenden einfach erklärt. 

Um einen Bruch durch einen zweiten Bruch zu teilen, müssen wir zunächst den Kehrwert (auch Kehrbruch) des zweiten Bruchs bilden. Kehrwert bedeutet: Zähler und Nenner werden vertauscht.

Bruch: \dfrac{2}{3}
Kehrwert: \dfrac{3}{2}

Nachdem der Kehrwert des zweiten Bruchs gebildet wurde, muss auch das Rechenzeichen von einem Divisionszeichen in ein Malzeichen geändert werden. Im Anschluss multiplizieren wir beide Brüche. Dieses Vorgehen wird auch Kehrwertregel genannt.

Kehrwertregel bei der Division von Brüchen

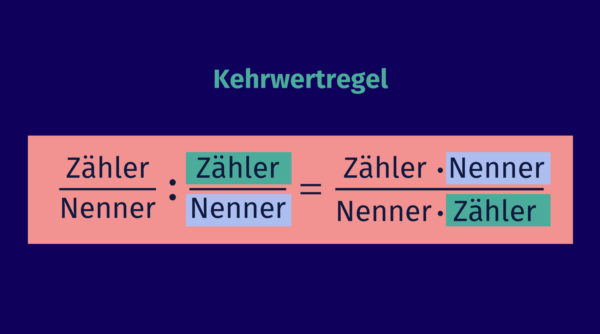
Brüche dividieren – Merksatz: Für die Division zweier Brüche multiplizieren wir den ersten Bruch mit dem Kehrwert des zweiten Bruchs.

Beispiel:
\dfrac{4}{5} : \dfrac{2}{3} = \dfrac{4}{5} \cdot \dfrac{3}{2} = \dfrac{12}{10} = \dfrac{6}{5}

Diese Vorgehensweise gilt sowohl, wenn wir gemeine Brüche dividieren, als auch bei der Division sogenannter unechter Brüche.
Auch bei der Division muss das Vorzeichen beachtet werden. Sind beide Brüche positiv oder beide Brüche negativ, ist das Ergebnis positiv. Ist ein Bruch positiv und ein Bruch negativ, ist das Ergebnis negativ.

Auf einen Beweis zur Formel für das Dividieren zweier Brüche wollen wir hier verzichten. Betrachten wir jedoch die folgende allgemeine Herleitung:

\dfrac{a}{b} : \dfrac{c}{d}

Wir teilen zunächst Zähler durch Zähler und Nenner durch Nenner. Im Anschluss erweitern wir die rechte Seite mit c und d.

\dfrac{a}{b} : \dfrac{c}{d} = \dfrac{a:c}{b:d} = \dfrac{a:c \cdot c \cdot d}{b:d \cdot c \cdot d}

Im Zähler haben sich das : c und \cdot c gegenseitig auf. Auch im Nenner fallen so das : d und \cdot d heraus. Stehen bleibt:

\dfrac{a:c \cdot c \cdot d}{b:d \cdot c \cdot d} = \dfrac{a \cdot d}{b \cdot c} = \dfrac{a}{b} \cdot \dfrac{d}{c}

Wir sehen, dass die Division zweier Brüche im Allgemeinen der Kehrwertregel entspricht, also der Multiplikation des ersten Bruchs mit dem Kehrwert des zweiten Bruchs.

Brüche dividieren – Rechenweg

Schauen wir uns im Folgenden an einem Beispiel den Rechenweg der Division zweier Brüche noch einmal genauer an.

\dfrac{2}{5} : \dfrac{1}{3}

Schritt 1: Kehrwert bilden
Zunächst müssen wir den Kehrwert des zweiten Bruchs bilden. Dafür vertauschen wir den Zähler und den Nenner.

\underbrace{\dfrac{1}{3}}_{Bruch} \quad \rightarrow \quad \underbrace{\dfrac{3}{1}}_{Kehrbruch}

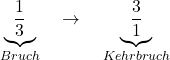
Schritt 2: Rechenzeichen verändern
Bevor wir weiter rechnen, müssen wir auch die Abänderung des Rechenzeichens beachten. Aus dem Geteiltzeichen wird ein Malzeichen.

\dfrac{2}{5} : \dfrac{1}{3} \quad \rightarrow \quad \dfrac{2}{5} \cdot \dfrac{3}{1}

Schritt 3: Brüche multiplizieren
Im Anschluss können wir beide Brüche miteinander multiplizieren. Dafür rechnen wir Zähler mal Zähler und Nenner mal Nenner.

\dfrac{2}{5} \cdot \dfrac{3}{1} = \dfrac{2 \cdot 3}{5 \cdot 1} = \dfrac{6}{5}

Für die Division von Brüchen ist es also wichtig, auch die Multiplikation von Brüchen zu beherrschen.

Brüche vor der Division kürzen

Wie bei der Multiplikation von Brüchen kann es auch bei der Division von Brüchen sinnvoll sein, zu schauen, ob sich diese bereits vor der Rechnung kürzen lassen.

Beispiel:

\dfrac{15}{18} : \dfrac{1}{4} = \dfrac{15 : 3}{18 : 3} : \dfrac{1}{4} = \dfrac{5}{6} \cdot \dfrac{4}{1} = \dfrac{20}{6} = \dfrac{10}{3}

Hier wurde der Dividend vor der Rechnung gekürzt.

Auch das Kürzen über Kreuz kann bei der Division angewandt werden. Dabei muss beachtet werden, dass man diese Art des Kürzens erst nach der Bildung des Kehrwerts durchführen kann, also wenn multipliziert wird.
Im folgenden Beispiel kann die 4 aus dem Nenner des ersten Bruchs mit der 4 aus dem Zähler des Kehrwerts des zweiten Bruchs gekürzt werden.

\dfrac{3}{4} : \dfrac{5}{4} = \dfrac{3}{\not{4}} \cdot \dfrac{\not{4}}{5} = \dfrac{3}{1} \cdot \dfrac{1}{5} = \dfrac{3}{5}

Besonders bei größeren Zahlen kann das Kürzen der Brüche vor dem Multiplizieren das Rechnen deutlich vereinfachen.

Brüche dividieren – Beispiele

Wir betrachten Beispiele für Quotienten, bei denen der Divisor oder der Dividend oder beide Zahlen Brüche sind. Dabei schreiben wir die Zahlen, wenn nötig, zunächst als Bruch um. Im Anschluss wird wie oben beschrieben der Kehrwert gebildet und dann Zähler mal Zähler und Nenner mal Nenner gerechnet. Die folgende Tabelle veranschaulicht verschiedene Szenarien, z. B. wie man eine ganze Zahl durch einen Bruch teilt oder wie mit Variablen bei der Division von Brüchen umgegangen wird.

Beispiel Rechnung Hinweis
Ganze Zahl durch Bruch dividieren 5 : \dfrac{2}{3} = \dfrac{5}{1} \cdot {3}{2} = \dfrac{15}{2} Die ganze Zahl muss vor der Division in einen Bruch umgewandelt werden.
Bruch mit ganzer Zahl dividieren \dfrac{2}{3} : 2 = \dfrac{2}{3} : \dfrac{2}{1} = \dfrac{2}{3} \cdot \dfrac{1}{2} = \dfrac{2}{6} = \dfrac{1}{3} Die ganze Zahl muss vor der Division in einen Bruch umgewandelt werden.
Bruch mit ganzer Zahl dividieren (Alternative) \dfrac{2}{3} : 2 = \dfrac{2}{3 \cdot 2} = \dfrac{2}{6} = \dfrac{1}{3} Alternativ kann man die ganze Zahl auch direkt in den Nenner des Bruchs ziehen und dort multiplizieren.
Gemischte Brüche dividieren 2 \dfrac{2}{3} : \dfrac{1}{4} = \dfrac{8}{3} : \dfrac{1}{4} = \dfrac{8}{3} \cdot \dfrac{4}{1} = \dfrac{32}{3} Die gemischte Zahl muss vor dem Dividieren in einen Bruch umgewandelt werden.
Brüche mit Variablen dividieren \dfrac{2}{5}\,x : \dfrac{3}{7}\,y = \dfrac{2\,x}{5} : \dfrac{3\,y}{7} = \dfrac{2\,x}{5} \cdot \dfrac{7}{3\,y} = \dfrac{14\,x}{15\,y} Die Variablen werden im allerersten Schritt, also vor der Bildung des Kehrwerts, in den Zähler des Bruchs geschrieben.

Häufig gestellte Fragen zum Thema Brüche dividieren

Um zwei Brüche durcheinander zu dividieren, muss zunächst der Kehrwert des zweiten Bruchs gebildet werden. Im Anschluss wird der erste Bruch mit dem Kehrwert des zweiten Bruchs multipliziert.

Bruchzahlen oder auch Brüche werden dividiert, indem man den Kehrwert des Divisors bildet. Danach wird der Dividend mit dem Kehrwert des Divisors multipliziert.

Vor der Division können wir schauen, ob der Zähler und der Nenner eines Bruchs einen gemeinsamen Teiler haben. Ist das der Fall, kann der Bruch mit dem gemeinsamen Teiler gekürzt werden. Danach wird der Kehrwert gebildet und die Brüche werden multipliziert. 

Aber auch das Kürzen über Kreuz ist möglich. Dieser Schritt kann durchgeführt werden, nachdem der Kehrwert gebildet wurde. Wie genau das funktioniert, erfährst du im Abschnitt zum Kürzen bei der Division. 

Der Kehrwert ist ein wichtiger Teil der Division von Brüchen. Um den Kehrwert zu bilden, tauscht man den Zähler und den Nenner eines Bruchs. Nachdem der Kehrwert des zweiten Bruchs gebildet wurde, tauscht man das Geteiltzeichen durch ein Malzeichen aus und multipliziert den ersten Bruch mit dem Kehrwert des zweiten Bruchs.

Bei der Division ist es wichtig, die Vorzeichen zu beachten. Ist einer der beiden Brüche negativ, ist das Ergebnis ebenfalls negativ. Sind beide Brüche negativ, ist das Ergebnis positiv.

Um eine ganze Zahl durch einen Bruch zu teilen, muss die ganze Zahl zunächst als Bruch geschrieben werden. Im Anschluss werden die restlichen Schritte der Division von Brüchen durchgeführt.

Um einen Bruch durch eine ganze Zahl zu dividieren, muss die ganze Zahl zunächst in einen Bruch umgewandelt werden. Im Anschluss bildet man den Kehrwert des zweiten Bruchs und multipliziert diesen mit dem ersten Bruch. Alternativ kann die ganze Zahl auch direkt in den Nenner des Bruchs gezogen und mit der dort stehenden Zahl multipliziert werden.

Ist der Dividend oder der Divisor eine gemischte Zahl, muss diese zunächst als Bruch geschrieben werden. Im Anschluss werden die normalen Schritte der Division von Brüchen durchgeführt.

Super! Das Thema: kannst du schon! Teile deine Learnings und Fragen mit der Community!

Alle Artikel aus dem Fach Mathematik