Additionsverfahren – Gleichungssysteme lösen: Erklärung und Beispiele

In Mathe wird das Additionsverfahren bei Aufgaben verwendet, die das Lösen eines linearen Gleichungssystems erfordern. Um ein lineares Gleichungssystem mit mehreren Variablen zu lösen, müssen wir die Anzahl der Variablen, die in einer Gleichung vorkommen, verringern. Beim Additionsverfahren geschieht dies, indem wir Gleichungen addieren.

Wie du allgemein vorgehen musst, wenn du ein lineares Gleichungssystem mit dem Additionsverfahren lösen möchtest, gehen wir nun an einem Beispiel durch.

Das Ergebnis ist eine Gleichung, die nur noch eine Variable enthält:

Wir können nach auflösen und erhalten . Dieses Ergebnis setzen wir nun in eine der beiden ursprünglichen Gleichungen ein, um die zweite Variable zu berechnen:

Die Lösung des Gleichungssystems ist das Wertepaar und .
Zur Probe können wir die berechneten Werte in eine der Gleichungen einsetzen:

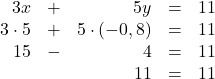
Wir erhalten eine wahre Aussage, damit stimmt das Ergebnis.

Nicht bei jedem Gleichungssystem fällt bei Addition der Gleichungen direkt eine der Variablen weg, so wie in unserem Einführungsbeispiel. Wir können aber jedes Gleichungssystem durch Multiplikation der Gleichungen mit geeigneten Faktoren auf eine solche Form bringen. Dabei ist das Ziel, dass eine der Variablen bei der Addition der Gleichungen wegfällt. Das bedeutet, die Koeffizienten dieser Variable müssen addiert ergeben. Dazu müssen die Koeffizienten den gleichen Betrag mit unterschiedlichem Vorzeichen aufweisen. Im Einführungsbeispiel sind das und , dadurch fällt bei der Addition die Variable weg.
Betrachten wir ein Beispiel, bei dem wir die richtige Form erst durch Multiplikation erzeugen müssen:

Wir möchten nun eliminieren und multiplizieren dafür die zweite Gleichung mit :

Nun können wir die Gleichungen addieren:

Wir berechnen :

Und setzen das Ergebnis in eine der ursprünglichen Gleichungen ein, um zu bestimmen:

Die Lösung des Gleichungssystems lautet:

und

Hinweis: Es gibt immer verschiedene Möglichkeiten, das Additionsverfahren auf ein Gleichungssystem anzuwenden. In unserem Beispiel hätte es sich auch angeboten, Gleichung durch zu teilen. Dies entspricht einer Multiplikation mit , es ist also auch eine Division zulässig.

Das Additionsverfahren kann auch bei linearen Gleichungssystemen mit mehr als zwei Variablen und Gleichungen angewendet werden. Dabei wird zum Beispiel bei einem linearen Gleichungssystem mit drei Gleichungen und drei Unbekannten zunächst eine der Gleichungen genutzt, um eine Variable aus den anderen beiden Gleichungen zu eliminieren. Damit hat sich das Problem auf zwei Gleichungen mit zwei Unbekannten reduziert, die wir wie gewohnt lösen können. Zuletzt wird diese Lösung dann in die dritte Gleichung eingesetzt, um den Wert der verbleibenden Variablen zu bestimmen.
Beispiel:

Wir nutzen Gleichung , um in den anderen beiden Gleichungen zu eliminieren:

Die Gleichung liefert bereits . Wir setzen den Wert in ein und erhalten:

Zuletzt setzen wir und in Gleichung ein und berechnen :

Ein systematisches Vorgehen zur Anwendung des Additionsverfahrens auf lineare Gleichungssysteme mit mehr als zwei Gleichungen ist das sogenannte gaußsche Eliminationsverfahren (auch Gauß-Algorithmus).