Dreiecke und Dreiecksarten einfach erklärt
Lerne alles über die Grundlagen, Arten und Berechnungen von Dreiecken. Von allgemeinen Dreiecken bis zu speziellen Linien und Flächenberechnungen. Interessiert? Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Dreiecke und Dreiecksarten
Das Quiz zum Thema: Dreiecke & Dreiecksarten
Welche sind die drei Dreiecksarten (anhand ihrer Winkel)?
Frage 1 von 5
Wie viele gleich lange Seiten hat ein gleichseitiges Dreieck?
Frage 2 von 5
Was gibt die Summe der Innenwinkel eines Dreiecks an?
Frage 3 von 5
Was ist die Bezeichnung für eine Gerade im Dreieck, die von der Mitte einer Seite zur gegenüberliegenden Ecke geht?
Frage 4 von 5
Welche Bedingung muss erfüllt sein, damit zwei Dreiecke als kongruent gelten?
Frage 5 von 5
Wie willst du heute lernen?
Allgemeines Dreieck – Definition, Beschriftung und Eigenschaften
Bei einem Dreieck handelt es sich um eine ebene geometrische Figur. Es besitzt drei Ecken und drei Seiten. Die Ecken werden mit Großbuchstaben gegen den Uhrzeigersinn beschriftet. Oft werden die Buchstaben ![]() ,
, ![]() und
und ![]() verwendet. Die Seiten des Dreiecks bezeichnen wir mit Kleinbuchstaben entsprechend der gegenüberliegenden Ecke, beispielsweise
verwendet. Die Seiten des Dreiecks bezeichnen wir mit Kleinbuchstaben entsprechend der gegenüberliegenden Ecke, beispielsweise ![]() ,
, ![]() und
und ![]() , wobei die Seite
, wobei die Seite ![]() der Ecke
der Ecke ![]() , die Seite
, die Seite ![]() der Ecke
der Ecke ![]() und die Seite
und die Seite ![]() der Ecke
der Ecke ![]() gegenüberliegen. Die Innenwinkel sind mit Buchstaben des griechischen Alphabets beschriftet, zum Beispiel
gegenüberliegen. Die Innenwinkel sind mit Buchstaben des griechischen Alphabets beschriftet, zum Beispiel ![]() ,
, ![]() und
und ![]() . Der Innenwinkel
. Der Innenwinkel ![]() befindet sich dabei am Eckpunkt
befindet sich dabei am Eckpunkt ![]() , der Winkel
, der Winkel ![]() am Eckpunkt
am Eckpunkt ![]() und der Winkel
und der Winkel ![]() am Eckpunkt
am Eckpunkt ![]() .
.

Eigenschaften eines Dreiecks:
- Die Innenwinkelsumme eines Dreiecks beträgt immer
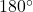 . Es gilt:
. Es gilt:
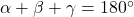
- Für die Außenwinkel des Dreiecks gilt, dass diese immer so groß wie die Summe der beiden nicht anliegenden Winkel sind.
- Im Dreieck liegt die längste Seite immer dem größten Winkel und die kürzeste Seite dem kleinsten Winkel gegenüber.
Kongruenzsätze im Dreieck
Passen zwei Dreiecke genau aufeinander, werden sie deckungsgleich oder kongruent genannt. Sie können dafür auch gedreht werden. Die Kongruenzsätze geben verschiedene Bedingungen vor, mit denen man prüfen kann, ob zwei Dreiecke kongruent sind.
| Kongruenzsatz | Bedeutung |
|---|---|
| SSS | Alle drei Seiten der Dreiecke sind gleich groß. |
| SWS | Zwei Seiten und der eingeschlossene Winkel stimmen genau überein. |
| WSW | Zwei Winkel an einer Seite sind gleich. |
| SSW | Zwei Seiten und der Winkel, der der längeren Seite gegenüberliegt, sind gleich. |
Ist eine der vier Bedingungen erfüllt, sind die zwei Dreiecke kongruent zueinander.
Die Kongruenzsätze können auch eine Grundlage beim Konstruieren von Dreiecken darstellen, da mindestens drei Informationen über das Dreieck (Seitenlängen, Winkelgrößen) bekannt sein müssen, um es zeichnen zu können.
Besondere Linien im Dreieck
Neben den drei Seiten existieren im Dreieck noch die Höhe, die Mittelsenkrechte, die Seitenhalbierende und die Winkelhalbierende
- Höhe: eine auf der Seite senkrecht stehende Gerade, die zur gegenüberliegenden Ecke geht
- Mittelsenkrechte: eine senkrechte Gerade, die durch die Mitte der Seite geht
- Seitenhalbierende: eine Gerade, die von der Mitte der Seite zur gegenüberliegenden Ecke geht
- Winkelhalbierende: eine Gerade, die den Winkel in zwei gleich große Hälften teilt
Höhenschnittpunkt
Da ein Dreieck immer drei Höhen besitzt, entsteht der sogenannte Höhenschnittpunkt. So wird der Punkt bezeichnet, an dem sich alle drei Höhen schneiden. Je nach Art des Dreiecks ist die Lage dieses Höhenschnittpunkts verschieden.
- Spitzwinkliges Dreieck: Höhenschnittpunkt liegt innerhalb des Dreiecks
- Stumpfwinkliges Dreieck: Höhenschnittpunkt liegt außerhalb des Dreiecks
- Rechtwinkliges Dreieck: Höhenschnittpunkt liegt auf dem Eckpunkt am rechten Winkel
Umkreis und Inkreis eines Dreiecks
Der Umkreis ist der Kreis, auf dem alle Eckpunkte des Dreiecks liegen. Es ist der kleinste Kreis, der das gesamte Dreieck einschließt. Der Mittelpunkt des Umkreises ist der Schnittpunkt aller drei Mittelsenkrechten. Um den Umkreis zu konstruieren, gehen wir folgendermaßen vor:
- Alle drei Mittelsenkrechten konstruieren
- Schnittpunkt der Mittelsenkrechten als Mittelpunkt des Umkreises festlegen
- Der Radius des Umkreises ist nun der Abstand des Schnittpunkts zu einem der drei Eckpunkte.
- Kreis mit dem Zirkel zeichnen, er sollte durch alle drei Eckpunkte gehen.
Bei dem Inkreis handelt es sich um den größten Kreis, der komplett im Dreieck liegt. Er berührt alle drei Seiten des Dreiecks. Der Inkreis eines Dreiecks lässt sich mithilfe der Winkelhalbierenden konstruieren.
- Alle drei Winkelhalbierenden konstruieren
- Der Schnittpunkt aller drei Winkelhalbierenden ist der Mittelpunkt des Inkreises.
- Der Radius des Inkreises ist nun der Abstand vom Schnittpunkt zu einer Seite des Dreiecks (dem nächsten Punkt der Seite).
- Kreis mit dem Zirkel zeichnen, er sollte die Seiten nicht schneiden, nur berühren und komplett innerhalb des Dreiecks liegen.
Dreiecksarten und ihre Eigenschaften
Dreiecke besitzen verschiedene Formen, nach denen sie in Kategorien eingeteilt werden können. Wir betrachten hier sechs gängige Arten von Dreiecken. Dabei klassifizieren wir die Dreiecke nach ihren Winkeln oder ihren Seiten. Die folgende Aufzählung bietet eine Übersicht über die gängigen Dreiecksarten.
Dreiecksarten nach ihren Winkeln klassifiziert:
- Stumpfwinkliges Dreieck: Ein Innenwinkel ist größer als
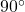 .
. - Spitzwinkliges Dreieck: Alle Innenwinkel sind kleiner als
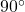 .
. - Rechtwinkliges Dreieck: Ein Innenwinkel ist genau
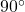 .
.
Dreiecksarten nach ihren Seiten klassifiziert:
- Ungleichmäßiges Dreieck: Alle Seiten sind verschieden lang.
- Gleichschenkliges Dreieck: Zwei Seiten sind gleich lang.
- Gleichseitiges Dreieck: Alle drei Seiten sind genau gleich lang.
Anhand ihrer Seitenverhältnisse oder der Winkel lassen sich die verschiedenen Dreiecksarten erkennen. Die folgende Grafik zeigt Beispiele für die verschiedenen Dreiecksformen und die dazugehörigen Namen der Dreiecksarten.

Stumpfwinkliges Dreieck
Als stumpfer Winkel wird ein Winkel bezeichnet, der größer als ![]() ist. Ein stumpfwinkliges Dreieck besitzt einen stumpfen Winkel. Dieser ist zwischen
ist. Ein stumpfwinkliges Dreieck besitzt einen stumpfen Winkel. Dieser ist zwischen ![]() und
und ![]() groß. Durch den Innenwinkelsatz ist gegeben, dass ein Dreieck maximal einen stumpfen Winkel besitzen kann. Dem stumpfen Winkel liegt immer die längste Seite gegenüber.
groß. Durch den Innenwinkelsatz ist gegeben, dass ein Dreieck maximal einen stumpfen Winkel besitzen kann. Dem stumpfen Winkel liegt immer die längste Seite gegenüber.
Spitzwinkliges Dreieck
Als spitzer Winkel wird ein Winkel bezeichnet, der kleiner als ![]() ist. In einem spitzwinkligen Dreieck sind alle drei Winkel kleiner als
ist. In einem spitzwinkligen Dreieck sind alle drei Winkel kleiner als ![]() .
.
Rechtwinkliges Dreieck
Als rechter Winkel wird ein Winkel bezeichnet, der genau ![]() ist. Ein rechtwinkliges Dreieck besitzt einen rechten Winkel. Auch hier ist durch den Innenwinkelsatz gegeben, dass ein Dreieck nur einen rechten Winkel besitzen kann. Dieser liegt immer der längsten Seite gegenüber. Diese längste Seite, die dem rechten Winkel gegenüberliegt, wird im rechtwinkligen Dreieck als Hypotenuse bezeichnet. Die beiden am rechten Winkel anliegenden Seiten nennen wir Katheten.
ist. Ein rechtwinkliges Dreieck besitzt einen rechten Winkel. Auch hier ist durch den Innenwinkelsatz gegeben, dass ein Dreieck nur einen rechten Winkel besitzen kann. Dieser liegt immer der längsten Seite gegenüber. Diese längste Seite, die dem rechten Winkel gegenüberliegt, wird im rechtwinkligen Dreieck als Hypotenuse bezeichnet. Die beiden am rechten Winkel anliegenden Seiten nennen wir Katheten.
Satz des Pythagoras
Der Satz des Pythagoras gibt die Beziehung der drei Seiten eines rechtwinkligen Dreiecks an. Er besagt:
Wichtig ist hierbei, dass ![]() die Hypotenuse, also die längste Seite, ist. Das ist immer die Seite, die dem rechten Winkel gegenüberliegt. Zudem gilt der Satz des Pythagoras nur in rechtwinkligen Dreiecken.
die Hypotenuse, also die längste Seite, ist. Das ist immer die Seite, die dem rechten Winkel gegenüberliegt. Zudem gilt der Satz des Pythagoras nur in rechtwinkligen Dreiecken.
Somit lässt sich im rechtwinkligen Dreieck die dritte Seitenlänge mithilfe der anderen beiden berechnen.
Der Satz des Thales besagt, dass ein Dreieck ![]() einen rechten Winkel besitzt, wenn der Punkt
einen rechten Winkel besitzt, wenn der Punkt ![]() auf einem Kreis mit dem Durchmesser
auf einem Kreis mit dem Durchmesser ![]() liegt. Dieser Satz kann genutzt werden, um ein rechtwinkliges Dreieck zu konstruieren.
liegt. Dieser Satz kann genutzt werden, um ein rechtwinkliges Dreieck zu konstruieren.
Seitenverhältnisse
Im rechtwinkligen Dreieck sind die Verhältnisse zwischen Winkeln und Seitenlänge festgelegt. Sie definieren die Winkelfunktionen Sinus (![]() ), Cosinus (
), Cosinus (![]() ) und Tangens (
) und Tangens (![]() ) für jeden der beiden spitzen Winkel. Dabei bezeichnet der Begriff Ankathete die am Winkel anliegende Kathete, der Begriff Gegenkathete bezeichnet die dem Winkel gegenüberliegende Kathete.
) für jeden der beiden spitzen Winkel. Dabei bezeichnet der Begriff Ankathete die am Winkel anliegende Kathete, der Begriff Gegenkathete bezeichnet die dem Winkel gegenüberliegende Kathete.
Die Winkelfunktionen lauten:
Sinus, Cosinus und Tangens ergeben sich also aus dem Verhältnis zweier Seiten zueinander. Sind ![]() und
und ![]() die beiden spitzen Winkel, können die Winkelfunktionen geschrieben werden als:
die beiden spitzen Winkel, können die Winkelfunktionen geschrieben werden als:
Der Sinus von ![]() entspricht also dem Cosinus von
entspricht also dem Cosinus von ![]() und der Cosinus von
und der Cosinus von ![]() entspricht dem Sinus von
entspricht dem Sinus von ![]() .
.
![]()
![]()
Unregelmäßiges Dreieck
Als ungleichmäßiges Dreieck wird ein Dreieck bezeichnet, das drei unterschiedlich lange Seiten besitzt. Es wird auch als ungleichseitiges Dreieck bezeichnet. Es gilt:
Gleichschenkliges Dreieck
Sind zwei Seiten eines Dreiecks gleich lang, sprechen wir von einem gleichschenkligen Dreieck. Die beiden gleich langen Seiten werden als Schenkel bezeichnet, die dritte Seite als Basis. Zudem besitzt das gleichschenklige Dreieck auch zwei gleich große Winkel, die sogenannten Basiswinkel. Sie liegen an der Basis an und damit je einem der Schenkel gegenüber. Bei dem gleichschenkligen Dreieck handelt es sich um ein symmetrisches Dreieck.
Ein gleichschenkliges Dreieck kann zusätzlich auch einen rechten Winkel besitzen. Dieser kann jedoch nur zwischen den beiden Schenkeln liegen. Das ist der Fall, wenn die beiden Basiswinkel je ![]() groß sind. Ein solches Dreieck kann dann gleichschenkliges, rechtwinkliges Dreieck genannt werden.
groß sind. Ein solches Dreieck kann dann gleichschenkliges, rechtwinkliges Dreieck genannt werden.
Gleichseitiges Dreieck
Bei einem gleichseitigen Dreieck sind alle drei Seiten genau gleich lang. Es gilt:
Somit sind auch alle drei Winkel genau gleich groß. Da durch den Innenwinkelsatz gegeben ist, dass alle drei Winkel zusammen ![]() ergeben, sind die einzelnen Winkel
ergeben, sind die einzelnen Winkel ![]() groß.
groß.
Dadurch handelt es sich bei dem gleichseitigen Dreieck auch immer um ein symmetrisches Dreieck.
Umfang eines Dreiecks berechnen
Beim Umfang handelt es sich um eine Längenangabe. Der Umfang gibt an, wie lang die Strecke einmal um das Dreieck herum ist, wenn man sich genau auf den Seiten des Dreiecks bewegt. Der Umfang eines Dreiecks lässt sich berechnen, indem alle drei Seitenlängen addiert werden. Die Formel zur Berechnung des Umfangs ![]() eines Dreiecks lautet:
eines Dreiecks lautet:
Im rechtwinkligen Dreieck kann der Umfang auch berechnet werden, wenn uns nur zwei der drei Seiten gegeben sind. Mithilfe des Satzes des Pythagoras kann die fehlende Seitenlänge ermittelt und somit der Umfang berechnet werden.
Flächeninhalt eines Dreiecks berechnen
Der Flächeninhalt ![]() gibt die vom Dreieck eingeschlossene Fläche an. Er lässt sich mit der folgenden Formel berechnen:
gibt die vom Dreieck eingeschlossene Fläche an. Er lässt sich mit der folgenden Formel berechnen:
Hierbei ist ![]() die Grundseite des Dreiecks. Du kannst dafür eine beliebige Seite des Dreiecks wählen. In den meisten Fällen wird die Seite genutzt, die sich unten befindet und horizontal verläuft. Bei
die Grundseite des Dreiecks. Du kannst dafür eine beliebige Seite des Dreiecks wählen. In den meisten Fällen wird die Seite genutzt, die sich unten befindet und horizontal verläuft. Bei ![]() handelt es sich um die senkrecht auf
handelt es sich um die senkrecht auf ![]() stehende Höhe.
stehende Höhe.
Flächeninhalt eines rechtwinkliges Dreieck berechnen
Für den Flächeninhalt des rechtwinkligen Dreiecks benötigen wir keine Höhe. Hier können statt ![]() und
und ![]() die Katheten, also die am rechten Winkel anliegenden Seiten, verwendet werden.
die Katheten, also die am rechten Winkel anliegenden Seiten, verwendet werden.
Liegt der rechte Winkel beispielsweise am Eckpunkt ![]() , wird er von den Seiten
, wird er von den Seiten ![]() und
und ![]() eingeschlossen. Die Formel für den Flächeninhalt lautet dann folgendermaßen:
eingeschlossen. Die Formel für den Flächeninhalt lautet dann folgendermaßen:
![]()
Flächeninhalt eines gleichschenkligen Dreiecks berechnen
Auch für das gleichschenklige Dreieck existiert eine Formel, die nur von zwei Seitenlängen abhängig ist. Dabei ist ![]() die Länge der gleich langen Schenkel und
die Länge der gleich langen Schenkel und ![]() die Länge der Basis.
die Länge der Basis.
![]()
Flächeninhalt eines gleichseitigen Dreiecks berechnen
Für das gleichseitige Dreieck kann die folgende Formel zur Berechnung des Flächeninhalts verwendet werden:
![]()
Hierbei bezeichnet ![]() die Länge einer Seite. Da alle drei Seiten gleich lang sind, ist es egal, welche der Seiten in die Formel eingesetzt wird.
die Länge einer Seite. Da alle drei Seiten gleich lang sind, ist es egal, welche der Seiten in die Formel eingesetzt wird.
Weitere Tipps findest du in unserer ausführlichen Anleitung zur Berechnung des Flächeninhalts von Dreiecken.
Weitere Berechnungen im Dreieck
Weitere Berechnungen im Dreieck sind:
- der Höhensatz,
- der Kathetensatz,
- der Sinus- und der Cosinussatz und
- die Berechnung der Höhe eines Dreiecks.
Höhe eines Dreiecks berechnen
Die Höhe eines Dreiecks ist eine Strecke, die senkrecht auf einer der drei Seiten steht und in der gegenüberliegenden Ecke endet. Somit gibt es drei verschiedene Höhen, die senkrecht auf ![]() stehende Höhe
stehende Höhe ![]() , die senkrecht auf
, die senkrecht auf ![]() stehende Höhe
stehende Höhe ![]() und die senkrecht auf
und die senkrecht auf ![]() stehende Höhe
stehende Höhe ![]() . Es gibt für alle drei Höhen zwei Formeln zur Berechnung:
. Es gibt für alle drei Höhen zwei Formeln zur Berechnung:
![]()
![]()
![]()
Sind keine der Winkel angegeben, kann die Höhe auch ohne diese ermittelt werden. Dafür wird zunächst ![]() berechnet:
berechnet:
![]()
Mithilfe dieser Größe können die drei verschiedenen Höhen berechnet werden:
![]()
![]()
![]()
Höhe im gleichseitigen Dreieck berechnen
Da alle Seiten und alle drei Winkel im gleichseitigen Dreieck genau gleich groß sind, sind auch die drei Höhen genau identisch. Es gilt:
![]()
Die Höhe eines gleichseitigen Dreiecks lässt sich mit der folgenden Formel berechnen:
![]()
Höhe im rechtwinkligen Dreieck berechnen
Im rechtwinkligen Dreieck teilt die auf der Hypotenuse stehende Höhe diese in zwei Abschnitte. Diese sogenannten Hypotenusenabschnitte werden mit ![]() und
und ![]() beschriftet. Der Höhensatz für rechtwinklige Dreiecke besagt nun:
beschriftet. Der Höhensatz für rechtwinklige Dreiecke besagt nun:
![]()
Sind ![]() und
und ![]() nicht gegeben, kann die Höhe im rechtwinkligen Dreieck selbstverständlich auch mit den anderen Formeln berechnet werden.
nicht gegeben, kann die Höhe im rechtwinkligen Dreieck selbstverständlich auch mit den anderen Formeln berechnet werden.
Häufig gestellte Fragen zum Thema Dreiecke und Dreiecksarten









Alle Artikel aus dem Fach Mathematik