Kommutativgesetz der Addition und Multiplikation einfach erklärt
Lerne, wie das Kommutativgesetz dir in der Mathematik hilft, Summanden und Faktoren zu vertauschen, ohne das Ergebnis zu ändern. Entdecke Anwendungen in Brüchen, Matrizen und Mengen. Interessiert? Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Kommutativgesetz
Das Kommutativgesetz im Überblick
Quelle sofatutor.com
Rechengesetze in der Mathematik – Kommutativgesetz
Die wichtigsten Rechenregeln in Mathe heißen Gesetze. Zu ihnen gehören zum Beispiel das Assoziativgesetz und das Distributivgesetz ebenso wie das Kommutativgesetz, das wir hier genauer betrachten wollen.
Der Name Kommutativgesetz hat die Bedeutung Vertauschungsgesetz vom lateinischen Verb commutare, was „vertauschen“ bedeutet. Im Folgenden wird erklärt, was wir wo vertauschen dürfen.
Kommutativgesetz der Addition – Definition
Das Kommutativgesetz der Addition besagt, dass wir bei einer Summe die Summanden vertauschen dürfen, ohne dass sich das Ergebnis verändert.
Auf einen formalen Beweis für das Kommutativgesetz der Addition wollen wir verzichten und uns dafür seine Gültigkeit mit der folgenden Darstellung veranschaulichen.
Wenn wir 
rechnen, erhalten wir das gleiche Ergebnis wie bei der Rechnung mit den vertauschten Summanden 
. Beide Rechnungen haben das Ergebnis 
.
Kommutativgesetz der Multiplikation – Definition
Das Kommutativgesetz der Multiplikation besagt, dass wir bei einem Produkt die Faktoren vertauschen dürfen, ohne dass sich dabei das Ergebnis verändert.
Auch das können wir uns an einem Beispiel veranschaulichen:
und 
Kommutativgesetz – Subtraktion und Division
Für die Subtraktion und Division gilt das Kommutativgesetz dagegen nicht. Hier ändert sich das Ergebnis einer Aufgabe in der Regel durch eine Vertauschung:
, aber 
, aber 
Unterschied – Assoziativgesetz und Kommutativgesetz
Das Assoziativgesetz und das Kommutativgesetz gelten beide bei der Addition und Multiplikation. Dabei besagt das Assoziativgesetz, dass sich das Ergebnis nicht ändert, wenn Klammern gesetzt werden, es wird auch Klammergesetz genannt. Nach dem Kommutativgesetz bleibt das Ergebnis einer Rechnung gleich, wenn Summanden oder Faktoren vertauscht werden, es wird auch Vertauschungsgesetz genannt.
Betrachten wir mögliche Berechnungen von 
:
Assoziativgesetz:
Kommutativgesetz:
Kommutativgesetz – Anwendungen und Beispiele
Allgemein sind Elemente einer Rechnung kommutativ, wenn ihr Vertauschen das Ergebnis nicht ändert. Dafür gibt es verschiedene Anwendungen, die wir hier kurz mit ein paar Beispielen betrachten wollen.
Kommutativgesetz bei Termen
Das Kommutativgesetz gilt auch bei der Addition und Multiplikation von Termen.
Beispiel:
Kommutativgesetz bei Brüchen
Auch die Addition und Multiplikation von Brüchen ist kommutativ. Oft kannst du hier durch das Vertauschen geschickt kürzen oder leichter einen gemeinsamen Nenner finden.
Beispiel:
Da Prozentzahlen als Brüche oder Dezimalzahlen dargestellt werden können, gilt das Kommutativgesetz folglich auch in der Prozentrechnung.
Kommutativgesetz bei Matrizen
Bei Matrizen gilt das Kommutativgesetz der Addition, die Matrizenmultiplikation ist aber nicht kommutativ. Eine Ausnahme sind die Multiplikation von Matrizen mit Skalaren und das Skalarprodukt von Vektoren.
Beispiel Kommutativgesetz beim Skalarprodukt:
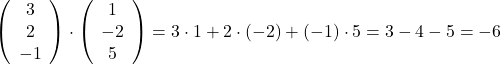
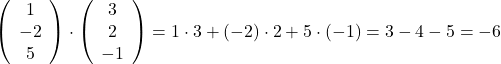
Kommutativgesetz bei Mengen
Für Mengen gilt das Kommutativgesetz bezüglich Schnitt und Vereinigung:
Hingegen ist die Differenz von Mengen nicht kommutativ. Wir betrachten ein Gegenbeispiel zum Beweis, dass das Kommutativgesetz bei der Differenz von Mengen nicht gilt:
Bei den Mengen 
und 
liefern die Differenzen unterschiedliche Mengen:
Häufig gestellte Fragen zum Kommutativgesetz
Das Kommutativgesetz ist ein Rechengesetz in der Mathematik.
Das Kommutativgesetz gilt bei der Addition und bei der Multiplikation.
Das Kommutativgesetz für Addition und Multiplikation lautet:
Das Kommutativgesetz besagt, dass die Summanden einer Addition oder die Faktoren einer Multiplikation vertauscht werden können. Das Ergebnis der Rechnung bleibt nach der Vertauschung unverändert.
Das Kommutativgesetz gilt bei der Addition und Multiplikation von reellen Zahlen.
Bei Mengen sind der Schnitt und die Vereinigung kommutativ. Bei Matrizen kann das Kommutativgesetz bei der Addition sowie der Multiplikation mit Skalaren angewendet werden. Außerdem gilt es beim Skalarprodukt von Vektoren.
Das Kommutativgesetz der Multiplikation lautet:
Für die Subtraktion gilt das Kommutativgesetz nicht. Es ist aber möglich, eine Differenz in eine Summe umzuschreiben und dann das Kommutativgesetz der Addition anzuwenden.
Beispiel: 
Drei wichtige Rechengesetze der Mathematik sind das Kommutativgesetz, das Assoziativgesetz und das Distributivgesetz.
Beim Assoziativgesetz können Klammern gesetzt werden, um die Reihenfolge der Berechnung zu ändern. Das Kommutativgesetz erlaubt es im Unterschied dazu, die Summanden oder Faktoren zu vertauschen.
Das Kommutativgesetz darf bei der Addition und bei der Multiplikation verwendet werden.
Das Kommutativgesetz darf bei der Addition und bei der Multiplikation verwendet werden.