Rotationskörper – Herleitung und Beispiele zu Volumen und Oberfläche

Ein Rotationskörper entsteht durch Drehung einer Fläche um eine Achse. Beispiele sind Zylinder, Kegel und Kugel. Die Berechnung von Volumen und Oberfläche erfolgt durch Integration. Entdecke die Vielfalt der Rotationskörper und lerne, wie man sie berechnet! Dies und mehr im folgenden Text.

Inhaltsverzeichnis zum Thema Rotationskörper

Rotationskörper im Überblick

  • Ein Rotationskörper entsteht durch Rotation einer Fläche um eine Achse.
  • Zylinder, Kegel und Kugel sind Rotationskörper.
  • Die Berechnung des Oberflächeninhalts und des Volumens von Rotationskörpern, die durch Rotation eines Funktionsgraphen um die x-Achse beschrieben werden, erfolgt durch Integration.
rotationskörper lernvideo, volumen von rotationskörpern lernvideo

Quelle sofatutor.com

Rotationskörper – Definition 

Ein Rotationskörper ist in Mathe einfach erklärt ein Körper, der durch Drehung einer Fläche um eine Rotationsachse entsteht. Der Schwerpunkt eines Rotationskörpers liegt auf der Rotationsachse.
Beispielsweise entsteht durch Rotation eines Rechtecks um eine Seitenfläche ein Zylinder. Wird ein rechtwinkliges Dreieck um eine seiner Katheten rotiert, ergibt sich ein Kegel.

Rotationskörper berechnen

Oberflächeninhalt und Volumen eines Rotationskörpers, der sich aus einfachen Körpern wie zum Beispiel Zylindern und Kegeln zusammensetzt, können mit den Formeln für diese Körper berechnet werden. Dabei wird der Rotationskörper für die Volumenberechnung in leicht zu berechnende Teilkörper zerlegt. Bei der Bestimmung der Oberfläche muss zudem beachtet werden, welche Flächen der Teilkörper gegenseitig überdeckt werden. 

Rotationskörper, die uns im Alltag zum Beispiel in Form von Vasen oder Flaschen begegnen, können häufig nicht so einfach in bekannte Körper zerlegt werden. Wie wir für solche Rotationskörper Volumen und Oberfläche mithilfe von Integralen berechnen können, betrachten wir im Folgenden.

Integration und Rotationskörper

Rotationskörper können durch Rotation eines Funktionsgraphen um die x-Achse beschrieben werden. Dabei wird das Flächenstück, das der Funktionsgraph in einem Intervall mit der x-Achse einschließt, rotiert. Der Funktionsgraph entspricht dann dem Verlauf der Außenkontur eines Querschnitts.
Ist der Funktionsterm f(x) des rotierenden Graphen bekannt, kann das rotierende Flächenstück durch Integration bestimmt werden. Auch die Formeln für das Volumen und die Oberfläche des Rotationskörpers enthalten ein Integral.

Rotationskörper – Volumen berechnen

Wir wollen die Formel für das Volumen eines Rotationskörpers, auch Rotationsvolumen genannt, allgemein herleiten. Dazu betrachten wir folgenden Körper, der sich durch Rotation des Graphen einer Funktion f(x) im Intervall \left[a, b\right] um die x-Achse ergibt.

Rotationskörper Funktionsgraph

Quelle sofatutor.com

Wir nähern das Volumen des Rotationskörpers, indem wir das Intervall in fünf gleich große Abschnitte unterteilen. Für jeden Abschnitt wählen wir einen Zylinder der Höhe h = \dfrac{b - a}{5}, dessen Radius r dem Funktionswert an der unteren Grenze des Abschnitts entspricht.

Rotationskörper Herleitung Volumen

Jeder dieser fünf Zylinder hat dann das Volumen:
V_{Z_i} = \pi \cdot r^2 \cdot h = \pi \cdot \bigl(f(x_i)\bigr)^2 \cdot \frac{b - a}{5}
Das Volumen des Rotationskörpers können wir folgendermaßen als Summe schreiben:
V_R = \sum\limits_{i = 0}^{4} \pi \cdot \bigl(f(x_i)\bigr)^2 \cdot \frac{b - a}{5}
Dabei erhalten wir eine immer genauere Näherung, je feiner wir das Intervall \left[a, b\right] unterteilen. Für n gleich große Teilstücke erhalten wir:
V_R = \sum\limits_{i = 0}^{n-1} \pi \cdot \bigl(f(x_i)\bigr)^2 \cdot \frac{b - a}{n}
Wir bilden den Grenzwert für n \to \infty und erhalten für das Volumen:
V_R = \lim \limits_{n \to \infty} \sum\limits_{i = 0}^{n-1} \pi \cdot \bigl(f(x_i)\bigr)^2 \cdot \frac{b - a}{n} = \int\limits_{a}^{b} \pi \cdot \bigl(f(x)\bigr)^2~\text{d}x
Den Faktor \pi schreiben wir zuletzt vor das Integral und erhalten für das Rotationsvolumen:
V_R = \pi \cdot \int\limits_{a}^{b} \bigl(f(x)\bigr)^2~\text{d}x

Rotationskörper – Oberfläche berechnen

Die Oberfläche eines Rotationskörpers, der durch Rotation des Graphen der Funktion f(x) um die x-Achse im Intervall \left[a, b\right] entsteht, setzt sich im Allgemeinen aus einer Grundfläche, einer Deckfläche und der Mantelfläche zusammen. Es gilt:

  • Grundfläche: G = \bigl(f(a)\bigr)^2 \cdot \pi
  • Deckfläche: D = \bigl(f(b)\bigr)^2 cdot \pi
  • Mantelfläche: M = 2\pi \cdot \int\limits_{a}^{b} f(x) \sqrt{1 + \bigl(f^\prime(x)\bigr)^2} ~\text{d}x
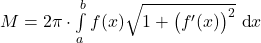
  • Oberfläche: O = G + D + M

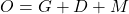
Die Grund- und Deckfläche sind dabei Kreise, deren Radien den Funktionswerten an den Intervallgrenzen entsprechen. Auf eine Herleitung der Formel für die Mantelfläche des Rotationskörpers wollen wir an dieser Stelle verzichten. Sie kann durch eine Zerlegung des Intervalls und eine anschließende Grenzwertbetrachtung erfolgen. Dabei sind die Teilkörper Kegelstümpfe.

Rotationskörper – Beispiel

Wir betrachten den Rotationskörper der linearen Funktion f(x) = 0,5x im Intervall \left[0, 5\right], dessen Volumen wir nun auf zwei Arten berechnen können.

Rotationskörper Beispiel
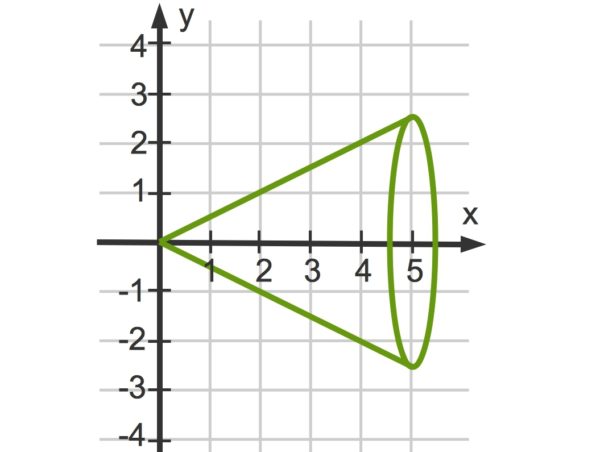
  • Der Körper ist ein Kegel mit der Höhe h = 5 und dem Radius der Grundfläche f(5) = 0,5 \cdot 5 = 2,5. Die Länge der Mantellinie s ist s = \sqrt{r^2 + h^2} = \frac{5\sqrt{5}}{2}. Damit erhalten wir:
    V = \dfrac{1}{3} \cdot r^2 \cdot \pi \cdot h = \dfrac{1}{3} \cdot 2,5^2 \cdot \pi \cdot 5 = \dfrac{125}{12}\pi
    O = G + M = r^2 \cdot \pi + r \cdot \pi \cdot s = 2,5^2 \cdot \pi + 2,5 \cdot \pi \cdot \dfrac{5\sqrt{5}}{2} \approx 63,54
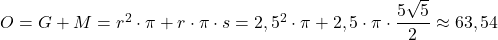
  • Das Rotationsvolumen der Funktion 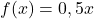f(x) = 0,5x im Intervall \left[0, 5\right] ist:
    \begin{array}{rl} V = & \pi \cdot \int\limits_{a}^{b} \bigl(f(x)\bigr)^2~\text{d}x \\ = & \pi \cdot \int\limits_{0}^{5} \bigl(0,5x\bigr)^2~\text{d}x \\ = & \pi \cdot \int\limits_{0}^{5} 0,25x^2~\text{d}x \\ = & \pi \cdot \Bigl[\frac{1}{4 \cdot 3}x^3\Bigr]_{0}^{5} \\ = & \pi \cdot \frac{1}{12} \cdot 5^3 \\ = & \frac{125}{12}\pi \end{array}
    Für die Oberfläche ergibt sich mit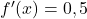 f^\prime(x) = 0,5:
    \begin{array}{rccc} O = & G & + & M \\ = & \bigl(f(b)\bigr)^2 \cdot \pi & + & 2\pi \cdot \int\limits_{a}^{b} f(x) \sqrt{1 + \bigl(f^\prime(x)\bigr)^2} ~\text{d}x \\ = & \bigl(0,5 \cdot 5\bigr)^2 \cdot \pi & + & 2\pi \cdot \int\limits_{0}^{5} 0,5x \sqrt{1 + \bigl(0,5\bigr)^2} ~\text{d}x \\ = & 6,25 \pi & + & 2\pi \cdot \int\limits_{0}^{5} \frac{\sqrt{5}}{4}x ~\text{d}x \\ = & 6,25 \pi & + & 2\pi \cdot \Bigl[\frac{\sqrt{5}}{4 \cdot 2}x^2\Bigr]_{0}^{5} \\ = & 6,25 \pi & + & \frac{25\sqrt{5}}{4}\pi \\ \approx && 63,54 \end{array}

Wir erhalten mit beiden Ansätzen ein Volumen von V = \frac{125}{12}\pi \approx 32,7 und eine Oberfläche von O \approx 63,54.
Hinweis: Bei einem Rotationskörper, der durch Rotation der Fläche zwischen zwei Funktionen entsteht, müssen die Rotationsvolumen beider Funktionsgraphen zunächst einzeln bestimmt und dann subtrahiert werden. Es ist nicht zulässig, die Differenz der Funktionen in die Formel für das Rotationsvolumen einzusetzen, da dies aufgrund des Quadrats zu einem falschen Ergebnis führt.

Häufig gestellte Fragen zum Thema Rotationskörper

Ein Rotationskörper ist ein Körper, der durch Rotation einer Fläche um eine Rotationsachse beschrieben werden kann.

Zur Berechnung von Volumen und Oberfläche von Rotationskörpern gibt es verschiedene Formeln.
Beispielsweise gilt für den Rotationskörper eines Rechtecks mit den Seitenlängen a und b, das um die Seite b rotiert: Es ist ein Zylinder mit h = b und r = a. Dieser hat dann das Volumen V = r^2 \cdot \pi \cdot h = a^2 \cdot \pi \cdot b.
Wird ein Rotationskörper durch einen Funktionsgraphen gebildet, kann bei der Berechnung das Integral genutzt werden.

Ein Rotationskörper entsteht durch Drehung einer Fläche um eine Achse. Dies kann etwa ein Rechteck sein, das um eine seiner Seiten rotiert, oder auch die Fläche, die ein Funktionsgraph mit der x-Achse in einem Intervall einschließt und die um die x-Achse rotiert.

Um einen Rotationskörper zu skizzieren, wird die rotierende Fläche an der Rotationsachse gespiegelt. Die Grund- und Deckfläche sind Kreise, die als Ellipsen über der unteren und oberen Kante der Figur dargestellt werden. 

Ein Quader ist kein Rotationskörper. Durch Rotation eines Quadrats um eine seiner Seiten entsteht stets ein Zylinder.

Eine Kugel ist ein Rotationskörper, der durch Rotation eines Halbkreises um den Durchmesser entsteht.

Die Betrachtung und Berechnung von Rotationskörpern erfolgte bereits durch Mathematiker im antiken Griechenland.

Ein Kegel entsteht durch Rotation eines rechtwinkligen Dreiecks um eine seiner Katheten.

Ein Rotationskörper entsteht durch Drehung einer Fläche um eine Rotationsachse.

Das Volumen eines Rotationskörpers, der durch Rotation des Graphen der Funktion f(x) um die x-Achse im Intervall \left[a, b\right] entsteht, kann mit einem Integral berechnet werden.
Es gilt:
V_R = \pi \cdot \int\limits_{a}^{b} \bigl(f(x)\bigr)^2~\text{d}x

Unter den besonderen Körpern sind Zylinder, Kegel und Kugel Rotationskörper. Allgemein gilt jeder Körper als Rotationskörper, der sich durch Rotation einer Fläche um eine Rotationsachse beschreiben lässt.

Leave A Comment

Alle Artikel aus dem Fach Mathematik