Funktionen Mathematik – Übersicht
Lerne, was eine Funktion definiert, wie Funktionsgleichungen funktionieren und wie man Funktionsgraphen interpretiert. Finde heraus, welche Eigenschaften, Typen und Veränderungen es bei Funktionen gibt. Interessiert? Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Funktionen
Teste dein Wissen
Was ist eine Funktion?
Frage 1 von 5
Was ist der Definitionsbereich einer Funktion?
Frage 2 von 5
Wie viele Arten von Funktionen gibt es?
Frage 3 von 5
Wie kann ich eine Funktion zeichnen?
Frage 4 von 5
Was versteht man unter der Funktionsgleichung?
Frage 5 von 5
Funktionen – einfach erklärt
Funktionen ordnen jedem ![]() -Wert genau einen
-Wert genau einen ![]() -Wert zu. Es handelt sich nicht um eine Funktion, wenn ein
-Wert zu. Es handelt sich nicht um eine Funktion, wenn ein ![]() -Wert zwei oder mehr
-Wert zwei oder mehr ![]() -Werte besitzt.
-Werte besitzt.
Jedem Element aus der Definitionsmenge ![]() (
(![]() -Werte) wird also eindeutig ein Element aus der Wertemenge
-Werte) wird also eindeutig ein Element aus der Wertemenge ![]() (
(![]() -Werte) zugeordnet. Funktionen stellen somit eine Beziehung zwischen zwei Mengen dar.
-Werte) zugeordnet. Funktionen stellen somit eine Beziehung zwischen zwei Mengen dar.
![]() mit
mit ![]() und
und ![]()
Dabei bezeichnet ![]() den Funktionswert an einer Stelle
den Funktionswert an einer Stelle ![]() . Deswegen wird
. Deswegen wird ![]() auch geschrieben als
auch geschrieben als ![]() (ausgesprochen:
(ausgesprochen: ![]() von
von ![]() ). Die Rechenvorschrift, mit der sich zu jedem
). Die Rechenvorschrift, mit der sich zu jedem ![]() -Wert der dazugehörige
-Wert der dazugehörige ![]() -Wert berechnen lässt, heißt Funktionsgleichung.
-Wert berechnen lässt, heißt Funktionsgleichung.
Mathematische Funktion – Beispiel: ![]()
Der Funktionswert ![]() ist immer abhängig von
ist immer abhängig von ![]() . Daher wird
. Daher wird ![]() als unabhängige Variable und
als unabhängige Variable und ![]() als abhängige Variable bezeichnet.
als abhängige Variable bezeichnet.
Definitionsbereich von Funktionen
Die Menge an Werten, die für ![]() in die Funktionsgleichung eingesetzt werden dürfen, wird Definitionsbereich (Definitionsmenge)
in die Funktionsgleichung eingesetzt werden dürfen, wird Definitionsbereich (Definitionsmenge) ![]() genannt.
genannt.
Wertebereich von Funktionen
Die Menge aller ![]() -Werte, die eine Funktion annehmen kann, wird als Wertebereich (Wertemenge)
-Werte, die eine Funktion annehmen kann, wird als Wertebereich (Wertemenge) ![]() bezeichnet.
bezeichnet.
Funktionswert berechnen
Der Funktionswert ist immer einem ![]() -Wert zugeordnet. Setzt man für das
-Wert zugeordnet. Setzt man für das ![]() in der Funktion eine Zahl aus der Definitionsmenge ein, erhält man den zugehörigen Funktionswert.
in der Funktion eine Zahl aus der Definitionsmenge ein, erhält man den zugehörigen Funktionswert.
Beispiel: ![]()
Wir wollen den Funktionswert für ![]() berechnen. Dafür setzen wir
berechnen. Dafür setzen wir ![]() für
für ![]() in die Funktionsgleichung ein und berechnen
in die Funktionsgleichung ein und berechnen ![]() :
:
![]()
Funktionsgraph – Definition
Durch Anwendung der Funktionsgleichung ergeben sich Wertepaare bestehend aus einem ![]() -Wert und dem zugehörigen Funktionswert
-Wert und dem zugehörigen Funktionswert ![]() .
.
Beispiel: Das Wertepaar ![]() ist Teil der Funktion
ist Teil der Funktion ![]() .
.
Diese Wertepaare können in ein Koordinatensystem eingetragen werden. Zeichnest du mehrere Wertepaare ein und verbindest ihre Punkte miteinander, erhältst du den Funktionsgraphen. Funktionsgraphen sind die grafischen Darstellungen von Funktionen, umfassen also die Menge aller Wertepaare einer Funktion.
Beispiel: Der Funktionsgraph von ![]() verläuft durch die Punkte
verläuft durch die Punkte
 ,
, ,
,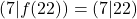 und
und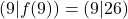 .
.

Charakteristische Punkte eines Funktionsgraphen
Jede Funktion verläuft anders, es gibt jedoch verschiedene Punkte, die eine Funktion haben kann, die sie charakterisiert. Die wichtigsten sind:
- Nullstellen: Punkte, an denen der Graph der Funktion die
 -Achse schneidet. Der Funktionswert ist an diesen Punkten null:
-Achse schneidet. Der Funktionswert ist an diesen Punkten null: 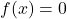 . Eine Funktion kann keine, eine oder mehrere Nullstellen besitzen.
. Eine Funktion kann keine, eine oder mehrere Nullstellen besitzen.  -Achsenabschnitt: Punkt, an dem der Graph der Funktion die
-Achsenabschnitt: Punkt, an dem der Graph der Funktion die  -Achse schneidet.
-Achse schneidet.  beträgt an diesen Punkten null:
beträgt an diesen Punkten null: 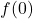 . Eine Funktion kann die
. Eine Funktion kann die  -Achse maximal einmal schneiden.
-Achse maximal einmal schneiden.- Maximum: höchster Punkt des Graphen der Funktion und damit größter
 -Wert der Funktion
-Wert der Funktion - Minimum: tiefster Punkt des Graphen der Funktion und damit kleinster
 -Wert der Funktion
-Wert der Funktion
Eigenschaften von Funktionen
Funktionen besitzen verschiedene Eigenschaften, die sie definieren. Die wichtigsten Eigenschaften sind:
- der Definitions- und Wertebereich,
- die charakteristischen Punkte des Funktionsgraphens,
- Monotonie, Periodizität und Symmetrie des Funktionsgraphens und
- die Grenzwerte der Funktion.
Funktionsarten
Es gibt viele verschiedene Arten von Funktionen, die alle unterschiedliche Eigenschaften besitzen. Im Folgenden werden verschiedene Funktionstypen, ihre Funktionsgraphen und besondere Merkmale aufgezeigt. Dies bietet eine Übersicht über die wichtigsten Funktionen und ihre Graphen.
Lineare Funktionen
In linearen Funktionen kommt ![]() nur mit der Potenz eins vor. Der Graph einer linearen Funktion ist eine Gerade im Koordinatensystem. Die Funktionsgleichung lautet allgemein:
nur mit der Potenz eins vor. Der Graph einer linearen Funktion ist eine Gerade im Koordinatensystem. Die Funktionsgleichung lautet allgemein:
![]()
Dabei ist:
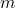 : die Steigung
: die Steigung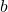 : der
: der  -Achsenabschnitt
-Achsenabschnitt

Quadratische Funktionen
In quadratischen Funktionen kommt ![]() als höchste Potenz vor. Der Funktionsgraph einer quadratischen Funktion heißt Parabel. Die allgemeine Form der Funktionsgleichung lautet:
als höchste Potenz vor. Der Funktionsgraph einer quadratischen Funktion heißt Parabel. Die allgemeine Form der Funktionsgleichung lautet:
![]()

Der höchste oder tiefste Punkt einer Parabel wird als Scheitelpunkt ![]() bezeichnet. Quadratische Funktionen können neben der allgemeinen Form auch in der Scheitelpunktform
bezeichnet. Quadratische Funktionen können neben der allgemeinen Form auch in der Scheitelpunktform ![]() geschrieben werden. Die Formen lassen sich ineinander umwandeln.
geschrieben werden. Die Formen lassen sich ineinander umwandeln.
Potenzfunktionen
Alle Funktionen der Form ![]() gehören zu den Potenzfunktionen. Dabei ist der Exponent
gehören zu den Potenzfunktionen. Dabei ist der Exponent ![]() stets eine ganze Zahl.
stets eine ganze Zahl.
Ihr grafischer Verlauf unterscheidet sich je nachdem, ob sie einen positiven, negativen, geraden oder ungeraden Exponenten haben.

Potenzfunktionen mit negativem Exponenten können auch als Brüche geschrieben werden:
![]()
Bei geradem Exponenten verläuft der Graph oberhalb der ![]() -Achse, bei ungeradem Exponenten liegt der Graph für negative
-Achse, bei ungeradem Exponenten liegt der Graph für negative ![]() -Werte unterhalb der
-Werte unterhalb der ![]() -Achse.
-Achse.
Hinweis: Potenzfunktionen mit positivem Exponenten gehören auch zu den ganzrationalen Funktionen. Solche mit negativem Exponenten gehören auch zu den gebrochen rationalen Funktionen.
Ganzrationale Funktionen
Ganzrationale Funktionen (Polynomfunktion) haben in ihrer Funktionsgleichung immer ein Polynom der Form:
![]()
mit ![]() ,
, ![]() und
und ![]()
Der höchste vorkommende Exponent ![]() gibt den Grad des Polynoms an.
gibt den Grad des Polynoms an.
Der Graph einer ganzrationalen Funktion besitzt maximal so viele Nullstellen wie der Grad der Funktion. Hier siehst du ein Beispiel für eine ganzrationale Funktion dritten Grads mit drei Nullstellen.

Gebrochen rationale Funktion
Bei gebrochen rationalen Funktionen besteht die Funktionsgleichung aus einem Bruch mit Polynomen im Zähler und Nenner. Sie haben die allgemeine Form:
![]()
Je nach Zählergrad und Nennergrad unterscheiden sich die Graphen der gebrochen rationalen Funktionen. Für Nullstellen des Nennerpolynoms ![]() ist die Funktion nicht definiert. Der Graph hat hier senkrechte Asymptoten.
ist die Funktion nicht definiert. Der Graph hat hier senkrechte Asymptoten.
Der Graph der einfachsten gebrochen rationalen Funktion ![]() ist hier dargestellt. Er wird auch Hyperbel genannt.
ist hier dargestellt. Er wird auch Hyperbel genannt.

Exponentialfunktionen
Hat eine Funktion die Form ![]() , handelt es sich um eine Exponentialfunktion. Die Variable
, handelt es sich um eine Exponentialfunktion. Die Variable ![]() steht hierbei im Exponenten. Bei Exponentialfunktionen bildet die
steht hierbei im Exponenten. Bei Exponentialfunktionen bildet die ![]() -Achse eine Asymptote.
-Achse eine Asymptote.
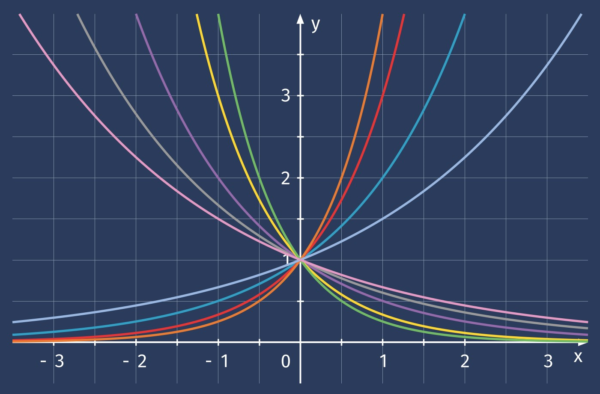
Die natürliche Exponentialfunktion hat die Basis ![]() und wird auch
und wird auch ![]() -Funktion genannt.
-Funktion genannt.
Logarithmusfunktion
Hat eine Funktion die Form ![]() , handelt es sich um eine Logarithmusfunktion. Bei Logarithmusfunktionen bildet die
, handelt es sich um eine Logarithmusfunktion. Bei Logarithmusfunktionen bildet die ![]() -Achse die Asymptote des Funktionsgraphen.
-Achse die Asymptote des Funktionsgraphen.
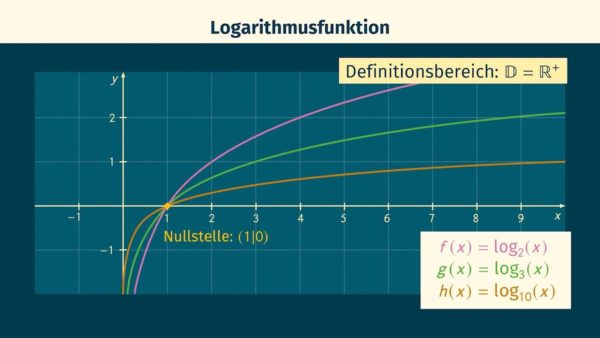
Trigonometrische Funktionen
Die drei trigonometrischen Funktionen sind die Sinusfunktion ![]() , die Cosinusfunktion
, die Cosinusfunktion ![]() und die Tangensfunktion
und die Tangensfunktion ![]() . Sie alle verlaufen periodisch.
. Sie alle verlaufen periodisch.

Betragsfunktion und Signum-Funktion
Wie weit eine Zahl auf dem Zahlenstrahl von der Null entfernt ist, wird durch die Betragsfunktion ![]() angegeben. Sie wird unter anderem zur Abstandsberechnung genutzt und besteht aus zwei Halbgeraden, die sich im Ursprung treffen.
angegeben. Sie wird unter anderem zur Abstandsberechnung genutzt und besteht aus zwei Halbgeraden, die sich im Ursprung treffen.
Die Signum-Funktion ist die Ableitung der Betragsfunktion. Sie wird auch als Vorzeichenfunktion bezeichnet, da sie das Vorzeichen einer Zahl angibt. Der Wertebereich umfasst nur die Zahlen ![]() ,
, ![]() und
und ![]() :
: ![]() . Die Funktion besitzt im Ursprung einen Sprung, ist dort also nicht stetig. Aus diesem Grund spricht man auch von der abschnittsweise definierten Funktion. Es gilt:
. Die Funktion besitzt im Ursprung einen Sprung, ist dort also nicht stetig. Aus diesem Grund spricht man auch von der abschnittsweise definierten Funktion. Es gilt:
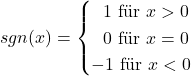
Veränderung von Grundfunktionen – Mathe
Durch verschiedene Parameter kann eine Grundfunktion modifiziert werden. Dadurch kann sich auch der Definitions- oder der Wertebereich ändern. Funktionen können verschoben, gestreckt, gestaucht oder gespiegelt werden.
Betrachten wir die quadratische Funktion ![]() als Grundfunktion.
als Grundfunktion.
Verschiebung in ![]() -Richtung
-Richtung
Um eine Funktion in Richtung der ![]() -Achse, also nach oben oder nach unten, zu verschieben, wird der Parameter
-Achse, also nach oben oder nach unten, zu verschieben, wird der Parameter ![]() zur Funktion addiert.
zur Funktion addiert.
![]()
Dabei gilt:
- Wenn
 positiv ist, verschiebt sich der Funktionsgraph um
positiv ist, verschiebt sich der Funktionsgraph um  Einheiten nach oben.
Einheiten nach oben. - Wenn
 negativ ist, verschiebt sich der Funktionsgraph um
negativ ist, verschiebt sich der Funktionsgraph um  Einheiten nach unten.
Einheiten nach unten.
Beispiel
Der Graph der Funktion ![]() ist im Vergleich zur Normalparabel
ist im Vergleich zur Normalparabel ![]() um
um ![]() Einheiten nach unten verschoben.
Einheiten nach unten verschoben.
Verschiebung in ![]() -Richtung
-Richtung
Um eine Funktion in Richtung der ![]() -Achse, also nach rechts oder nach links, zu verschieben, wird der Parameter
-Achse, also nach rechts oder nach links, zu verschieben, wird der Parameter ![]() direkt in die Funktionsgleichung eingefügt.
direkt in die Funktionsgleichung eingefügt.
![]()
Dabei gilt:
- Wenn
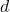 positiv ist, verschiebt sich der Funktionsgraph um
positiv ist, verschiebt sich der Funktionsgraph um 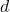 Einheiten nach links.
Einheiten nach links. - Wenn
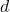 negativ ist, verschiebt sich der Funktionsgraph um
negativ ist, verschiebt sich der Funktionsgraph um 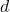 Einheiten nach rechts.
Einheiten nach rechts.
Beispiel
Der Graph der Funktion ![]() ist im Vergleich zur Normalparabel um
ist im Vergleich zur Normalparabel um ![]() Einheiten nach rechts verschoben.
Einheiten nach rechts verschoben.

Streckung und Stauchung von Funktionsgraphen
Wird ein Funktionsgraph gestreckt, bedeutet das, dass er steiler verläuft. Gestauchte Funktionsgraphen verlaufen weniger steil. Beides wird durch den Parameter ![]() beeinflusst.
beeinflusst.
![]()
Dabei gilt:
![]() : Der Funktionsgraph wird gestreckt.
: Der Funktionsgraph wird gestreckt.
![]() : Der Funktionsgraph wird gestaucht.
: Der Funktionsgraph wird gestaucht.
Beispiel
Der Graph der Funktion ![]() ist im Vergleich zur Normalparabel gestreckt, ist also schmaler und verläuft steiler.
ist im Vergleich zur Normalparabel gestreckt, ist also schmaler und verläuft steiler.
Spiegelung von Funktionsgraphen
Funktionen können an der ![]() -Achse gespiegelt werden. Wird
-Achse gespiegelt werden. Wird ![]() mit
mit ![]() multipliziert, wird die Funktion an der
multipliziert, wird die Funktion an der ![]() -Achse gespiegelt:
-Achse gespiegelt:
![]()
Bei achsensymmetrischen Funktionen verändert sich der Verlauf des Graphen nicht, da gilt: ![]() .
.
Beispiel
Der Graph der Funktion ![]() ist im Vergleich zum Graph der Funktion
ist im Vergleich zum Graph der Funktion ![]() an der
an der ![]() -Achse gespiegelt.
-Achse gespiegelt.
Funktionen können auch an der ![]() -Achse gespiegelt werden. Dann entsteht eine neue Funktion. Ist der Vorfaktor
-Achse gespiegelt werden. Dann entsteht eine neue Funktion. Ist der Vorfaktor ![]() negativ, wird die Funktion an der
negativ, wird die Funktion an der ![]() -Achse gespiegelt:
-Achse gespiegelt:
![]()
Beispiel
Der Graph der Funktion ![]() ist im Vergleich zur Normalparabel an der
ist im Vergleich zur Normalparabel an der ![]() -Achse gespiegelt.
-Achse gespiegelt.
Häufig gestellte Fragen zum Thema Funktionen

