Laplace-Experiment – Mathe
Ein Laplace-Experiment ist ein Zufallsversuch, bei dem alle Elementarereignisse die gleiche Wahrscheinlichkeit haben. Erfahre, wie die Laplace-Formel angewendet wird und welche Bedingungen erfüllt sein müssen. Dies und vieles mehr findest du im folgenden Text!
Inhaltsverzeichnis zum Thema Laplace-Experiment
Laplace-Experiment – Erklärung
Bei dem Laplace-Experiment handelt es sich um einen Zufallsversuch mit besonderen Merkmalen.
Zufallsversuch – Definition
Als Zufallsversuch (Zufallsexperiment) wird in Mathe ein Vorgang bezeichnet, der ohne Veränderung wiederholt werden kann. Der Ausgang des Experiments ist dabei unter den bekannten Möglichkeiten nicht vorhersehbar.
Ein Beispiel für ein Zufallsexperiment ist das Würfeln mit einem immer gleichen Würfel. Hier wissen wir, dass das Ergebnis eine der Zahlen des Würfels ist. Welches Ergebnis die einzelnen Würfe liefern, ist vorab jedoch nicht bekannt.
Ergebnis – Definition
Als Ergebnis (auch Elementarereignis) wird ein möglicher Ausgang eines Zufallsversuchs bezeichnet. Alle möglichen Ergebnisse sind in der Ergebnismenge ![]() zusammengefasst.
zusammengefasst.
Ereignis – Definition
Ein Ereignis ![]() umfasst eine beliebige Anzahl von Ergebnissen eines Zufallsexperiments, diese werden dann auch als für das Ereignis günstig bezeichnet. Dabei unterscheiden wir:
umfasst eine beliebige Anzahl von Ergebnissen eines Zufallsexperiments, diese werden dann auch als für das Ereignis günstig bezeichnet. Dabei unterscheiden wir:
- Unmögliches Ereignis:
 – es gibt keine günstigen Ergebnisse.
– es gibt keine günstigen Ergebnisse. - Elementarereignis:
 – es gibt genau ein günstiges Ergebnis.
– es gibt genau ein günstiges Ergebnis. - Mögliches Ereignis:
 – es gibt mindestens ein günstiges Ergebnis.
– es gibt mindestens ein günstiges Ergebnis. - Sicheres Ereignis:
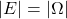 – alle Ergebnisse der Ergebnismenge
– alle Ergebnisse der Ergebnismenge 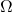 sind günstig.
sind günstig.
Laplace-Experiment – Definition
Ein Zufallsversuch, bei dem alle Elementarereignisse die gleiche Wahrscheinlichkeit haben, wird als Laplace-Experiment (Laplace-Versuch) bezeichnet.
Das bedeutet, dass ein Laplace-Experiment, neben den Voraussetzungen für den Zufallsversuch, die Bedingung erfüllt, dass alle Elementarereignisse gleich wahrscheinlich sind.
Laplace-Experiment – Formel
Mit der Laplace-Formel kann die Wahrscheinlichkeit einzelner Ereignisse berechnet werden. Diese Formel wird auch als Laplace-Regel bezeichnet. Dabei wird die Anzahl der günstigen Ergebnisse durch die Anzahl der möglichen Ergebnisse geteilt.
![]()
Dabei ist:
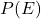 : Wahrscheinlichkeit des Ereignisses
: Wahrscheinlichkeit des Ereignisses 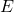
 : Anzahl der günstigen Ergebnisse
: Anzahl der günstigen Ergebnisse : Anzahl der möglichen Ergebnisse
: Anzahl der möglichen Ergebnisse
Als günstige Ergebnisse werden die Ergebnisse bezeichnet, die Teil der Ergebnismenge von Ereignis ![]() sind.
sind.
Beispiel:
Ist das gesuchte Ereignis das Würfeln einer geraden Zahl mit einem sechsseitigen Würfel, dann ist die Anzahl der günstigen Ergebnisse ![]() , da das Ereignis „gerade“ beim Würfeln der
, da das Ereignis „gerade“ beim Würfeln der ![]() , der
, der ![]() und der
und der ![]() eintritt. Die Anzahl der möglichen Ergebnisse ist
eintritt. Die Anzahl der möglichen Ergebnisse ist ![]() . Für die Wahrscheinlichkeit dieses Ereignisses ergibt sich nach der Laplace-Formel:
. Für die Wahrscheinlichkeit dieses Ereignisses ergibt sich nach der Laplace-Formel:
![]()
Solche Ereignisse werden auch als zusammengesetzte Ereignisse bezeichnet, da sie aus mehreren Elementarereignissen zusammengesetzt sind.
Für Elementarereignisse gibt es genau ein günstiges Ergebnis. Die Wahrscheinlichkeit für ein Elementarereignis ist damit nach der Laplace-Formel:
![]()
Beispiel:
Für den Wurf mit einem sechsseitigen Würfel gibt es ![]() Elementarereignisse. Da sich die Gesamtwahrscheinlichkeit gleichmäßig auf diese Ereignisse verteilt, ist die Wahrscheinlichkeit jedes der
Elementarereignisse. Da sich die Gesamtwahrscheinlichkeit gleichmäßig auf diese Ereignisse verteilt, ist die Wahrscheinlichkeit jedes der ![]() Ergebnisse:
Ergebnisse: ![]() .
.
Es gilt:
![]()

Laplace-Experiment – Zusammenfassung der Eigenschaften
Der Laplace-Versuch ist eine besondere Form der Zufallsversuche. Die folgende Tabelle zeigt, welche Eigenschaften erfüllt sein müssen, damit es sich um einen Zufallsversuch oder um einen Laplace-Versuch handelt.
| Bedingung | Zufallsversuch | Laplace-Versuch |
|---|---|---|
| Alle möglichen Ausgänge sind bekannt. | x | x |
| Der Ausgang ist nicht vorhersehbar. | x | x |
| Der Versuch kann beliebig oft wiederholt werden. | x | x |
| Die Bedingungen bei der Durchführung sind immer gleich. | x | x |
| Alle Elementarereignisse haben die gleiche Wahrscheinlichkeit. | x |
Das Besondere am Laplace-Versuch ist also die gleiche Wahrscheinlichkeit aller Elementarereignisse.
Die Formel zur Berechnung der Wahrscheinlichkeit ![]() eines Ereignisses
eines Ereignisses ![]() lautet:
lautet:
![]()
Laplace-Experiment – Beispiele
Ein typisches Beispiel für ein Laplace-Experiment ist das Werfen einer (Lapalce-)Münze. Dabei landet die Münze mit einer Wahrscheinlichkeit von je ![]() auf einer der beiden Seiten.
auf einer der beiden Seiten.
Auch das Drehen an einem Glücksrad, bei dem alle Felder gleich groß sind, ist ein Laplace-Experiment.
Im Folgenden wollen wir die Laplace-Formel an weiteren Beispielen anwenden.
Laplace-Experiment – Urne
Befinden sich in einer Urne nur gleich große Kugeln, wird jede Kugel mit der gleichen Wahrscheinlichkeit gezogen und es handelt sich um ein Laplace-Experiment.
Nehmen wir an, es befinden sich ![]() Kugeln in der Urne. Davon sind
Kugeln in der Urne. Davon sind ![]() Kugeln grün und
Kugeln grün und ![]() Kugeln rot. Mit welcher Wahrscheinlichkeit ziehst du eine rote Kugel
Kugeln rot. Mit welcher Wahrscheinlichkeit ziehst du eine rote Kugel ![]() ?
?
Die allgemeine Formel zur Berechnung der Wahrscheinlichkeit lautet:
![]()
Da sich ![]() Kugeln in der Urne befinden, ist die Anzahl aller möglichen Ergebnisse
Kugeln in der Urne befinden, ist die Anzahl aller möglichen Ergebnisse ![]() . Die Anzahl der günstigen Ergebnisse lautet
. Die Anzahl der günstigen Ergebnisse lautet ![]() , da
, da ![]() der Kugeln rot sind. Somit beträgt die Wahrscheinlichkeit für das Ereignis
der Kugeln rot sind. Somit beträgt die Wahrscheinlichkeit für das Ereignis ![]() : „eine rote Kugel wird gezogen“:
: „eine rote Kugel wird gezogen“:
![]()
Laplace-Experiment – Würfel
Betrachten wir einen ungezinkten sechsseitigen Würfel. Wie hoch ist die Wahrscheinlichkeit, eine Zahl zu würfeln, die durch ![]() teilbar ist?
teilbar ist?
Die Anzahl der möglichen Ergebnisse ist ![]() . Da nur die Zahlen
. Da nur die Zahlen ![]() und
und ![]() durch
durch ![]() teilbar sind, ist die Anzahl der günstigen Ergebnisse
teilbar sind, ist die Anzahl der günstigen Ergebnisse ![]() . Somit liegt die Wahrscheinlichkeit für das Ereignis
. Somit liegt die Wahrscheinlichkeit für das Ereignis ![]() : „teilbar durch drei“ bei:
: „teilbar durch drei“ bei:
![]()
Nicht-Laplace-Experimente – Beispiele
Als Gegenteil der Laplace-Experimente werden Zufallsexperimente bezeichnet, bei denen die Ereignisse nicht alle die gleiche Wahrscheinlichkeit besitzen. Bei diesen Experimenten kann die Laplace-Formel nicht angewandt werden.
Beispiele für ein Nicht-Laplace-Experiment sind das Würfeln mit einem gezinkten Würfel oder das Werfen einer Reißzwecke, die fast immer auf den Kopf fällt.
Häufig gestellte Fragen zum Thema Laplace-Experiment

