Dezimalzahlen und Dezimalbrüche in Prozente und Brüche umwandeln
Erfahre, wie Dezimalbrüche in Prozent und Brüche umgewandelt werden. Entdecke Periodische Dezimalzahlen, Rechenregeln mit Dezimalzahlen und Alltagsanwendungen.
Inhaltsverzeichnis zum Thema Dezimalbrüche
Teste dein Wissen
Was ist ein Dezimalbruch?
Frage 1 von 4
Wie wird eine Dezimalzahl in Prozent umgerechnet?
Frage 2 von 4
Was beschreibt eine periodische Dezimalzahl?
Frage 3 von 4
Welche Methode wird NICHT verwendet, um einen Bruch in einen Dezimalbruch umzuwandeln?
Frage 4 von 4
Dezimalbruch – Erklärung
Ein Dezimalbruch ist ein Bruch, dessen Nenner eine Zehnerpotenz ist, also ![]() ,
, ![]() ,
, ![]() …
…
Einen Dezimalbruch kann man sowohl in Bruchschreibweise als auch in Kommaschreibweise angeben. Die Anzahl der Nachkommastellen hängt dabei von der Zehnerpotenz ab. Steht im Nenner ![]() , entspricht das einer Nachkommastelle, steht im Nenner
, entspricht das einer Nachkommastelle, steht im Nenner ![]() , entspricht das zwei Nachkommastellen etc.
, entspricht das zwei Nachkommastellen etc.
Beispiele:
In Kommaschreibweise wird der Dezimalbruch häufig als Dezimalzahl oder Kommazahl bezeichnet. Eine Dezimalzahl besteht aus Vorkommastellen, einem Komma und Nachkommastellen. Die Stellenwerttafel wird dabei, wie im folgenden Bild dargestellt, nach rechts erweitert:

Die Stellenwerttafel hilft auch dabei, einen Dezimalbruch am Zahlenstrahl abzutragen. Der kleinste Stellenwert ist dabei ausschlaggebend dafür, wie fein der Zahlenstrahl aufgeteilt werden muss.
Hinweis: Häufig werden die Begriffe Dezimalzahl und Dezimalbruch gleichbedeutend verwendet. Dies ist aber nicht der Fall: Es gibt Dezimalzahlen, die auch als Brüche geschrieben werden können, die keine Zehnerpotenz im Nenner haben, diese schauen wir uns weiter unten an. Außerdem gibt es Dezimalzahlen, die gar nicht als Bruch dargestellt werden können, zum Beispiel die Kreiszahl ![]() .
.
Einen Bruch in einen Dezimalbruch umwandeln
Um einen Bruch als Dezimalbruch zu schreiben, wird der Bruch so erweitert, dass im Nenner eine Zehnerpotenz steht. Als Beispiel schreiben wir ![]() als Dezimalbruch:
als Dezimalbruch:
![]()
Da im Nenner nun eine ![]() steht, entspricht der Zähler der Zehntelstelle und in Dezimalschreibweise lautet der Bruch:
steht, entspricht der Zähler der Zehntelstelle und in Dezimalschreibweise lautet der Bruch:
![]()
Als zweites Beispiel möchten wir Dreiviertel, also ![]() , als Dezimalbruch schreiben:
, als Dezimalbruch schreiben:
![]()
Wir können den Dezimalbruch aufteilen, sodass wir die Stellenwerte einfach ablesen können:
![]()
Es sind also ![]() Zehntel und
Zehntel und ![]() Hundertstel. Der Dezimalbruch lautet somit in Kommaschreibweise:
Hundertstel. Der Dezimalbruch lautet somit in Kommaschreibweise:
![]()
Nicht alle Brüche lassen sich mit einer ganzzahligen Erweiterungszahl so erweitern, dass eine Zehnerpotenz im Nenner steht, oder es ist nicht so offensichtlich, welche Erweiterungszahl verwendet werden muss. Deswegen gibt es auch eine andere Möglichkeit, einen Bruch in eine Dezimalzahl umzuwandeln. Hierfür wird die schriftliche Division verwendet:

Die schriftliche Division endet hier nach der dritten Nachkommastelle. So kann mit der schriftlichen Division der Dezimalbruch berechnet werden.
Allgemein heißen Dezimalzahlen, für die die schriftliche Division nach endlich vielen Schritten keinen Rest mehr hat, endliche Dezimalzahlen oder abbrechende Dezimalzahlen.
Es lässt sich auch am Nenner direkt erkennen, ob der Bruch so erweiterbar ist, dass im Nenner eine Zehnerpotenz steht: Nur wenn der Nenner ausschließlich die Primfaktoren ![]() oder
oder ![]() hat, lässt sich ein Bruch so erweitern.
hat, lässt sich ein Bruch so erweitern.
Auch ein gemischter Bruch lässt sich in eine Dezimalzahl umwandeln. Dies geht entweder mit der schriftlichen Division oder indem der echte Bruch so erweitert wird, dass im Nenner eine Zehnerpotenz steht.
Beispiel: ![]()
Dezimalzahlen in Brüche umwandeln
Für die Umrechnung eines Dezimalbruchs in einen Bruch wird die Dezimalzahl ohne Komma in den Zähler geschrieben und die Zehnerpotenz entsprechend der letzten Nachkommastelle an der Stellenwerttafel bestimmt. Sind es zum Beispiel zwei Nachkommastellen, handelt es sich um Hundertstel und in den Nenner wird ![]() geschrieben:
geschrieben:
![]()
Der so entstandene Bruch kann dann noch gekürzt werden.
Periodische Dezimalzahlen
Nicht alle Dezimalzahlen sind abbrechende Dezimalzahlen. Beispielsweise lässt sich zwei Drittel, also ![]() , nicht als Dezimalbruch schreiben. Mithilfe der schriftlichen Division lässt sich aber die Kommazahl
, nicht als Dezimalbruch schreiben. Mithilfe der schriftlichen Division lässt sich aber die Kommazahl ![]() bestimmen.
bestimmen.
Als weiteres Gegenbeispiel schauen wir uns den Bruch ![]() an und führen dafür die schriftliche Division durch:
an und führen dafür die schriftliche Division durch:

Hier fällt auf, dass sich die Rechnung immer wiederholt. Wird ![]() durch
durch ![]() geteilt, bleibt der Rest
geteilt, bleibt der Rest ![]() , der wiederum zu
, der wiederum zu ![]() ergänzt wird etc. Es gibt unendlich viele Einser als Nachkommastellen.
ergänzt wird etc. Es gibt unendlich viele Einser als Nachkommastellen.
Da wir keine unendlich vielen Nachkommastellen aufschreiben können, gibt es eine Kurzschreibweise dafür: Es wird ein waagerechter Strich über die Nachkommastelle, die sich unendlich oft wiederholt, gesetzt, hier also:
![]()
Dezimalzahlen, bei denen sich ein Rechenschritt in der schriftlichen Division unendlich oft wiederholt, werden periodische Dezimalzahlen genannt. Der waagerechte Strich über den Zahlen wird Periodenstrich genannt, die Zahl unter dem Strich heißt Periode.
Gesprochen wird ![]() als „null Komma Periode eins“.
als „null Komma Periode eins“.
Die Periode kann auch aus mehreren Ziffern bestehen. In dem Fall wiederholt sich eine Abfolge von mehreren Schritten in der schriftlichen Division. Zum Beispiel ist der Bruch ![]() eine periodische Dezimalzahl:
eine periodische Dezimalzahl:
![]()
In den beiden obigen Beispielen beginnt die Periode direkt nach dem Komma. Solche Dezimalzahlen heißen rein periodische Dezimalzahlen.
Die Periode kann aber auch später beginnen, zum Beispiel:
![]()
Rechnen mit Dezimalzahlen
Nach der Einführung von Dezimalzahlen mit Definitionen verschiedener Arten von Dezimalzahlen betrachten wir nun, wie wir mit diesen Zahlen rechnen können.
Addieren und subtrahieren von Dezimalzahlen
Beim Addieren und Subtrahieren von Dezimalzahlen kann schriftlich addiert oder subtrahiert werden, indem die Zahlen stellengerecht untereinander geschrieben werden. Das Komma muss dabei auf der gleichen Höhe stehen. Auch beim Ergebnis muss das Komma an der gleichen Stelle gesetzt werden.
Dazu schauen wir uns ein Beispiel an:

Multiplizieren von Dezimalzahlen
Beim Multiplizieren von Dezimalzahlen gibt es Regeln für die folgenden unterschiedlichen Fälle:
Multiplikation einer Dezimalzahl mit …
- … einer Zehnerpotenz größer als
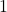 : In diesem Fall wird das Komma entsprechend der Anzahl der Nullen der Zehnerpotenz nach rechts verschoben. In manchen Fällen müssen dabei Nullen ergänzt werden.
: In diesem Fall wird das Komma entsprechend der Anzahl der Nullen der Zehnerpotenz nach rechts verschoben. In manchen Fällen müssen dabei Nullen ergänzt werden.
Beispiele: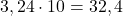 ;
; 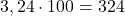 ;
; 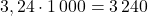
- … einer ganzen Zahl: Jede Stelle der Dezimalzahl wird mit der ganzen Zahl multipliziert. Dabei muss auf den Übertrag geachtet werden. Das Ergebnis hat genauso viele Nachkommastellen wie die Dezimalzahl.
- … einer anderen Dezimalzahl: Die Zahlen können schriftlich multipliziert werden, indem die schriftliche Multiplikation wie bei ganzen Zahlen stellenweise durchgeführt wird. Die Kommas werden dabei zunächst ignoriert. Nach dem Zusammenrechnen muss noch das Komma im Ergebnis gesetzt werden. Dafür werden die Nachkommastellen der beiden Faktoren addiert. Das Komma wird dann so gesetzt, dass das Ergebnis so viele Nachkommastellen hat wie beide Faktoren zusammen.
Dividieren von Dezimalzahlen
Bei der Division von Dezimalzahlen gibt es Regeln für die folgenden unterschiedlichen Fälle:
Der Dividend ist eine Dezimalzahl und …
- … der Divisor ist eine Zehnerpotenz größer als
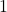 : In diesem Fall wird das Komma entsprechend der Anzahl der Nullen im Divisor nach links verschoben. In manchen Fällen müssen dabei Nullen ergänzt werden.
: In diesem Fall wird das Komma entsprechend der Anzahl der Nullen im Divisor nach links verschoben. In manchen Fällen müssen dabei Nullen ergänzt werden.
Beispiele: ;
;  ;
; 
- … der Divisor ist eine ganze Zahl: Der Quotient kann mit schriftlicher Division berechnet werden. Das Komma wird im Ergebnis gesetzt, wenn es in der Rechnung im Dividend erreicht wird.
- … der Divisor ist eine andere Dezimalzahl: Zunächst wird das Komma in beiden Zahlen um die gleiche Anzahl an Stellen nach rechts verschoben, bis im Divisor keine Zahlen mehr hinter dem Komma stehen. Dann wird wie durch eine ganze Zahl dividiert.
Dezimalzahlen runden
Dezimalbrüche können wie natürliche Zahlen aufgerundet und abgerundet werden. Dabei ist zunächst zu entscheiden, auf welchen Stellenwert gerundet werden soll. Es gelten die folgenden Regeln:
- Bei Zahlen kleiner als
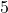 , also
, also 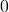 ,
, 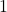 ,
, 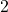 ,
, 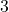 ,
, 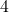 , wird abgerundet.
, wird abgerundet. - Bei Zahlen größer als oder gleich
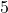 , also
, also 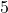 ,
, 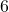 ,
, 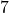 ,
, 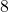 ,
, 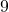 , wird aufgerundet.
, wird aufgerundet.
Beispiel:
Runde die Zahl ![]() …
…
- auf Ganze:

- auf Zehntel:

- auf Hundertstel:

- auf Tausendstel:

Damit lassen sich ebenso Rechnungen mit Dezimalzahlen überschlagen: Zunächst überlegen wir uns eine geeignete Stelle, auf die wir runden, und können dann die Rechnung überschlagen. Beispiel:
Wir möchten die Summe ![]() überschlagen und runden dafür auf Zehntel:
überschlagen und runden dafür auf Zehntel:
![]()
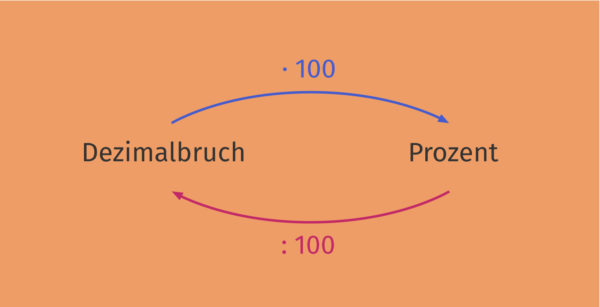
Einen Dezimalbruch in Prozent umrechnen und umgekehrt
Dezimalzahlen werden in Prozent umgerechnet, indem mit ![]() multipliziert wird. Wichtig dabei ist, dass bei Angabe in Prozent das Prozentzeichen
multipliziert wird. Wichtig dabei ist, dass bei Angabe in Prozent das Prozentzeichen ![]() ergänzt wird.
ergänzt wird.
Beispiel:
![]()
Der Dezimalbruch ![]() kann so als Prozentsatz
kann so als Prozentsatz ![]() angegeben werden.
angegeben werden.
Andersherum kann von Prozent in einen Dezimalbruch umgerechnet werden, indem durch ![]() dividiert wird. Dabei wird das Prozentzeichen weggelassen.
dividiert wird. Dabei wird das Prozentzeichen weggelassen.
Beispiele:
![]()
![]()
Brüche mithilfe von Dezimalzahlen in Prozent umwandeln
Wie wir in der Erklärung oben gesehen haben, können Dezimalzahlen einfach in Prozentzahlen umgewandelt werden. Deswegen wird beim Umwandeln von Brüchen in Prozent oft ein Zwischenschritt über die entsprechende Dezimalzahl vorgenommen. Das Vorgehen können wir so zusammenfassen:
- Bruch in Dezimalzahl umwandeln
- Dezimalzahl mit
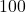 multiplizieren
multiplizieren
Beispiel:
![]()
Dieses Vorgehen gilt sowohl für abbrechende Dezimalzahlen als auch für periodische oder andere nicht abbrechende Dezimalzahlen. Wie berechnet man also ![]() in Prozent?
in Prozent?
![]()
So können auch periodische Dezimalzahlen in Prozent umgewandelt werden. Diese werden in Prozent häufig gerundet und nicht mit Periode angegeben.
Dezimalzahlen im Alltag
Dezimalzahlen kommen häufig in unserem Alltag vor, zum Beispiel werden Geldbeträge und Preise meistens in der Dezimalschreibweise angegeben, ebenso wie andere Maßeinheiten.
Zeit in Dezimalzahlen
Weil Zeiteinheiten nicht im Zehnersystem angegeben werden, gibt es einige Besonderheiten zu beachten, zum Beispiel beim Umrechnen von Dezimalzahlen in Minuten und umgekehrt.
Möchten wir beispielsweise eine Minute als Dezimalzahl in Stunden angeben, müssen wir den Bruch ![]() in eine Dezimalzahl umwandeln. Mithilfe der schriftlichen Division erhalten wir die periodische Dezimalzahl
in eine Dezimalzahl umwandeln. Mithilfe der schriftlichen Division erhalten wir die periodische Dezimalzahl ![]() . Es ist also
. Es ist also ![]() . So können wir jede Minutenzahl in Stunden umwandeln, indem wir mit der Dezimalzahl für eine Minute multiplizieren.
. So können wir jede Minutenzahl in Stunden umwandeln, indem wir mit der Dezimalzahl für eine Minute multiplizieren.
Beispiel:
![]()
Möchten wir eine Stundenzahl in Tage oder Sekunden in Stunden umwandeln, gehen wir nach dem gleichen Prinzip vor.
Häufig gestellte Fragen zum Thema Dezimalbruch

