Erwartungswert – Definition, Bedeutung und Berechnung
Der Erwartungswert zeigt den durchschnittlichen zu erwartenden Wert bei einem Zufallsversuch an. Lerne, wie man ihn berechnet und welche Eigenschaften er hat.
Inhaltsverzeichnis zum Thema Erwartungswert
Einführung Erwartungswert
Der Erwartungswert ist ein Begriff aus der Stochastik. Er gibt an, welcher Wert, also welches Ergebnis, bei einem Zufallsversuch im Mittel zu erwarten ist.
Betrachten wir als Beispiel den Münzwurf: Beim Ergebnis Kopf bekommt der Spieler ![]() Euro und bei Zahl bekommt er
Euro und bei Zahl bekommt er ![]() Euro. Intuitiv ist klar, dass der Spieler auf lange Sicht im Mittel
Euro. Intuitiv ist klar, dass der Spieler auf lange Sicht im Mittel ![]() Euro bekommt.
Euro bekommt.
Eine Herleitung dieses Erwartungswerts erfolgt nun mithilfe der allgemeinen Formel zur Berechnung des Erwartungswerts.
Berechnung des Erwartungswerts bei diskreten Verteilungen
Bei einer diskreten Verteilung kann die Zufallsvariable ![]() nur abzählbar viele Werte annehmen. Bei dem oben betrachteten Beispiel des Münzwurfs handelt es sich also um eine diskrete Verteilung, da die Zufallsvariable
nur abzählbar viele Werte annehmen. Bei dem oben betrachteten Beispiel des Münzwurfs handelt es sich also um eine diskrete Verteilung, da die Zufallsvariable ![]() genau zwei Werte annehmen kann:
genau zwei Werte annehmen kann: ![]() und
und ![]() .
.
Bei einem Zufallsversuch mit der Zufallsvariablen ![]() , die allgemein die Werte
, die allgemein die Werte ![]() annehmen kann, lautet die Formel zu Berechnung des Erwartungswerts
annehmen kann, lautet die Formel zu Berechnung des Erwartungswerts ![]() :
:
Um den Erwartungswert zu bestimmen, benötigen wir also die Wahrscheinlichkeiten ![]() für das Auftreten der einzelnen Ausprägungen
für das Auftreten der einzelnen Ausprägungen ![]() der Zufallsvariable.
der Zufallsvariable.
Da die Wahrscheinlichkeiten beim Münzwurf für Kopf und Zahl jeweils ![]() betragen, ergibt sich für den Erwartungswert:
betragen, ergibt sich für den Erwartungswert:
![]()
Beim Glücksspiel unterscheidet man zwischen einem fairen Spiel und einem nicht fairen Spiel. Beim fairen Spiel gleichen sich Gewinne und Verluste auf lange Sicht aus. Ein nicht faires Spiel hingegen verläuft auf lange Sicht zugunsten des Spielers oder der Bank.
Definiert man die Zufallsgröße als Differenz zwischen Einsatz und Gewinn, ist der Erwartungswert bei einem fairen Spiel gleich ![]() .
.
Hinweis: In der Regel gewinnt beim Glücksspiel auf lange Sicht die Bank und nicht der Spieler!
Erwartungswert einer diskreten Verteilung – Beispiele
Erwartungswert einfach erklärt am Beispiel eines Glücksrads
Ein Glücksrad wird einmal gedreht. Die Ergebnismenge für das unten abgebildete Glücksrad lautet:
![]()

Die Wahrscheinlichkeiten lauten:
![]()
![]()
![]()
An einem Stand zahlt Jurek einen Euro Einsatz und darf dann das Glücksrad einmal drehen. Bei rot bekommt er ![]() Cent, bei blau
Cent, bei blau ![]() Cent und bei gelb
Cent und bei gelb ![]() Euro zurück. Wir definieren die Zufallsvariable
Euro zurück. Wir definieren die Zufallsvariable ![]() als Differenz aus Gewinn und Einsatz:
als Differenz aus Gewinn und Einsatz:
| Ergebnis des Experiments | Ausprägung der Zufallsgröße |
Wahrscheinlichkeit |
|---|---|---|
| rot | ||
| blau | ||
| gelb |
Wir können nun den Erwartungswert mit der Formel berechnen:
![]()
Der negative Erwartungswert von ![]() bedeutet, dass Jurek im Schnitt einen Verlust von
bedeutet, dass Jurek im Schnitt einen Verlust von ![]() Cent macht. Das Spiel ist daher nicht fair.
Cent macht. Das Spiel ist daher nicht fair.
Erwartungswert beim Würfel
Wir betrachten als Beispiel den Erwartungswert ![]() beim Würfel. Die Ergebnismenge beim Werfen eines normalen Spielwürfels ist:
beim Würfel. Die Ergebnismenge beim Werfen eines normalen Spielwürfels ist:
![]()
Wir können nun mithilfe der Formel den Erwartungswert beim Würfelversuch berechnen:
Da es sich um einen Laplace-Versuch handelt, sind die Wahrscheinlichkeiten für die sechs möglichen Ergebnisse beim Würfeln jeweils gleich ![]() . Wir sprechen daher auch von einer Gleichverteilung und berechnen den Erwartungswert wie folgt:
. Wir sprechen daher auch von einer Gleichverteilung und berechnen den Erwartungswert wie folgt:
![]()
Erwartungswert besonderer diskreter Verteilungen
Erwartungswert einer Konstanten
Noch einfacher ergibt sich der Erwartungswert bei einer Konstanten, also einer Größe, die nicht variiert wird: In diesem Fall ist der Erwartungswert die Konstante selbst.
Erwartungswert bei einer Bernoulli-Verteilung
Bei einer Bernoulli-Verteilung, bei der die Zufallsvariable ![]() nur zwei Werte annimmt, ist der Erwartungswert gleich der Erfolgswahrscheinlichkeit
nur zwei Werte annimmt, ist der Erwartungswert gleich der Erfolgswahrscheinlichkeit ![]() :
:
![]()
Erwartungswert einer Binomialverteilung
![]()
Der Erwartungswert gibt dabei an, wie viele Treffer bei ![]() -maliger Durchführung des Experiments im Mittel zu erwarten sind.
-maliger Durchführung des Experiments im Mittel zu erwarten sind.
Erwartungswert einer geometrischen Verteilung
Die Basis einer geometrischen Verteilung ist die Binomialverteilung. Dabei gehen wir bei der geometrischen Verteilung der Frage nach, wie oft das Experiment durchgeführt werden muss, bis der erste Erfolg eintritt. Der Erwartungswert ist hier:
![]()
Erwartungswert bei stetigen Verteilungen
Ist die Anzahl der möglichen Werte, die eine Zufallsvariable annehmen kann, unendlich, spricht man von einer stetigen Verteilung. In diesem Fall müssen wir den Erwartungswert als Integral
![]()
Dabei nennen wir die Funktion ![]() in der Formel des Erwartungswerts die Dichtefunktion.
in der Formel des Erwartungswerts die Dichtefunktion.
Wir müssen jedoch nicht immer das Integral berechnen, um den Erwartungswert einer Verteilungsfunktion zu bestimmen. Für viele Verteilungsfunktionen lässt sich in der Wahrscheinlichkeitsrechnung der Erwartungswert direkt angeben.
Erwartungswert der Normalverteilung
Die Normalverteilung ![]() ist über den Erwartungswert
ist über den Erwartungswert ![]() definiert. Wir können ihn also direkt aus der Formel ablesen.
definiert. Wir können ihn also direkt aus der Formel ablesen.
Erwartungswert der Dreiecksverteilung
Für eine dreiecksverteilte Zufallsvariable ![]() lautet der Erwartungswert:
lautet der Erwartungswert:
![]()
Übersicht Erwartungswerte besonderer Verteilungen
- Bernoulli-Verteilung: Erwartungswert
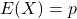
- Binomialverteilung: Erwartungswert

- Konstante
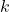 : Erwartungswert
: Erwartungswert 
- Geometrische Verteilung: Erwartungswert

- Normalverteilung
 : Erwartungswert
: Erwartungswert 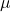
- Dreiecksverteilung: Erwartungswert

Erwartungswert – Eigenschaften
Für den Erwartungswert gelten einige Rechenregeln. Wir betrachten dazu die folgende Tabelle zum Erwartungswert:
| Summe von Erwartungswerten | |
|---|---|
| Produkt von Erwartungswerten | |
| Konstanten |
Weitere Größen zum Erwartungswert
Häufig wird die Streuung einer Größe um den Erwartungswert in der Mathematik untersucht, also die Abweichung vom Erwartungswert. Diese Größe nennt man die Varianz. Die Standardabweichung einer Zufallsgröße vom Erwartungswert ist die Wurzel aus der Varianz.
Sprechen wir von der Kovarianz beim Erwartungswert, beschreiben wir den Zusammenhang zweier Zufallsvariablen.
Im Zusammenhang mit bedingten Wahrscheinlichkeiten kann bei einem Zufallsexperiment auch ein bedingter Erwartungswert ermittelt werden. Wir sprechen dann als Abgrenzung auch vom totalen Erwartungswert bezogen auf die totalen Wahrscheinlichkeiten der Ergebnisse.
Auch in Bereichen außerhalb der Mathematik findet der Erwartungswert Anwendung, zum Beispiel wird in der Quantenmechanik mit dem Erwartungswert einer Wellenfunktion gearbeitet.
Häufig gestellte Fragen zum Erwartungswert

